1) j2—j1 = ±2mp (т=0, 1, 2, .), тогда A=A1+A2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний; 1 страница

Стр 1 из 14Следующая ⇒

ЭЛЕКТРИЧЕСТВО И ЭЛЕКТРОМАГНЕТИЗМ..... 116

Глава 11Электростатика. ............................................. 116

§ 77. Закон сохранения электрического заряда............................................... 116

§ 78. Закон Кулона................................................................................................ 117

§ 79. Электростатическое поле. Напряженность электростатического поля 117

§ 80. Принцип суперпозиции электростатических полей. Поле диполя..... 119

§ 81. Теорема Гаусса для электростатического поля в вакууме................... 120

§ 82. Применение теоремы Гаусса к расчету некоторых электростатических полей в вакууме..................................................................................................... 122

§ 83. Циркуляция вектора напряженности электростатического поля....... 124

§ 84. Потенциал электростатического поля..................................................... 125

§ 85. Напряженность как градиент потенциала. Эквипотенциальные поверхности............................................................................................................ 126

§ 86. Вычисление разности потенциалов по напряженности поля............... 127

§ 87. Типы диэлектриков. Поляризация диэлектриков.................................. 128

§ 88. Поляризованность. Напряженность поля в диэлектрике..................... 129

§ 88. Электрическое смещение. Теореме Гаусса для электростатического поля в диэлектрике............................................................................................................ 130

§ 90. Условия на границе раздела двух диэлектрических сред.................... 131

§ 91. Сегнетоэлектрики........................................................................................ 132

§ 92. Проводники в электростатическом поле................................................. 134

§ 93. Электрическая емкость уединенного проводника................................. 136

§ 94. Конденсаторы............................................................................................... 136

§ 95. Энергия системы зарядов, уединенного проводника и конденсатора. Энергия электростатического поля................................................................... 138

Задачи...................................................................................................................... 140

Глава 12Постоянный электрический ток 141

§ 96. Электрический ток, сила и плотность тока............................................. 141

§ 97. Сторонние силы. Электродвижущая сила и напряжение..................... 142

§ 98. Закон Ома. Сопротивление проводников................................................ 143

§ 99. Работа и мощность тока. Закон Джоуля — Ленца................................. 144

§ 100. Закон Ома для неоднородного участка цепи........................................ 145

§ 101. Правила Кирхгофа для разветвленных цепей...................................... 146

Задачи...................................................................................................................... 148

Глава 13 Электрические токи в металлах, вакууме и газах.............................. 148

§ 102. Элементарная классическая теория электропроводности металлов 148

§ 103. Вывод основных законов электрического тока в классической теории электропроводности металлов............................................................................ 149

§ 104. Работа выхода электронов из металла................................................... 151

§ 105. Эмиссионные явления и их применение................................................ 152

§ 106. Ионизация газов. Несамостоятельный газовый разряд...................... 154

§ 107. Самостоятельный газовый разряд и его типы...................................... 155

§ 108. Плазма и ее свойства................................................................................. 158

Задачи...................................................................................................................... 159

Глава 14 Магнитное поле. ...................... 159

§ 109. Магнитное поле и его характеристики.................................................. 159

§ 110. Закон Био — Савара — Лапласа и его применение к расчету магнитного поля.......................................................................................................................... 162

§ 111. Закон Ампера. Взаимодействие параллельных токов......................... 163

§ 112. Магнитная постоянная. Единицы магнитной индукции и напряженности магнитного поля.................................................................................................... 164

§ 113. Магнитное поле движущегося заряда................................................... 165

§ 114. Действие магнитного поля на движущийся заряд............................... 166

§ 115. Движение заряженных частиц в магнитном поле................................ 166

§ 116. Ускорители заряженных частиц............................................................. 167

§ 117. Эффект Холла............................................................................................ 169

§ 118. Циркуляция вектора В магнитного поля в вакууме............................ 169

§ 119. Магнитные поля соленоида и тороида.................................................. 171

§ 120. Поток вектора магнитной индукции. Теорема Гаусса для поля В.... 172

§ 121. Работа по перемещению проводника и контура с током в магнитном поле.................................................................................................................................. 172

Задачи...................................................................................................................... 174

Глава 15 Электромагнитная индукция. ......................................................................................... 174

§122. Явление электромагнитной индукции (опыты Фарадея).................... 174

§ 123. Закон Фарадея и его вывод из закона сохранения энергии................ 175

§ 124. Вращение рамки в магнитном поле........................................................ 177

§ 125. Вихревые токи (токи Фуко)..................................................................... 177

§ 126. Индуктивность контура. Самоиндукция............................................... 178

§ 127. Токи при размыкании и замыкании цепи............................................... 179

§ 128. Взаимная индукция................................................................................... 181

§ 129. Трансформаторы....................................................................................... 182

§ 130. Энергия магнитного поля........................................................................ 183

Глава 16 Магнитные свойства вещества. ............................................................................................ 184

§ 131. Магнитные моменты электронов и атомов........................................... 184

§ 132. Диа- и парамагнетизм................................................................................ 186

§ 133. Намагниченность. Магнитное поле в веществе.................................... 187

§ 134. Условия на границе раздела двух магнетиков..................................... 189

§ 135. Ферромагнетики и их свойства............................................................... 190

§ 136. Природа ферромагнетизма...................................................................... 191

Глава 17 Основы теории Максвелла для электромагнитного поля. ................................................. 193

§ 137. Вихревое электрическое поле................................................................. 193

§ 138. Ток смещения............................................................................................. 194

§ 139. Уравнения Максвелла для электромагнитного поля.......................... 196

........................................................................................................................................ 198

Глава 18 Механические и электромагнитные колебания. ............................... 198

§ 140. Гармонические колебания и их характеристики.................................. 198

§ 141. Механические гармонические колебания............................................. 200

§ 142. Гармонический осциллятор. Пружинный, физический и математический маятники.................................................................................................................. 201

§ 143. Свободные гармонические колебания в колебательном контуре.... 203

§ 144. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения..................................................................................................... 205

§ 145. Сложение взаимно перпендикулярных колебаний............................. 206

§ 146. Дифференциальное уравнение свободных затухающих колебаний (механических и электромагнитных) и его решение. Автоколебания......... 208

§ 147. Дифференциальное уравнение вынужденных колебаний (механических и электромагнитных) и его решение..................................................................... 211

§ 148. Амплитуда и фаза вынужденных колебаний (механических и электромагнитных). Резонанс............................................................................. 213

§ 148. Переменный ток......................................................................................... 215

§ 150. Резонанс напряжений................................................................................ 217

§ 151. Резонанс токов........................................................................................... 218

§ 152. Мощность, выделяемая в цепи переменного тока............................... 219

Глава 19Упругие волны. ..................................................... 221

§ 153. Волновые процессы. Продольные и поперечные волны.................... 221

§ 154. Уравнение бегущей волны. Фазовая скорость. Волновое уравнение 222

§ 155. Принцип суперпозиции. Групповая скорость...................................... 223

§ 156. Интерференция волн................................................................................. 224

§ 157. Стоячие волны........................................................................................... 225

§ 158. Звуковые волны......................................................................................... 227

S 159. Эффект Доплере в акустике..................................................................... 228

§ 160. Ультразвук и его применение.................................................................. 229

Глава 20Электромагнитные волны...................................................................... 230

§ 161. Экспериментальное получение электромагнитных волн................... 230

§ 162. Дифференциальное уравнение электромагнитной волны. ....................................................... 232

§ 163. Энергия электромагнитных волн. Импульс электромагнитного поля 233

§ 164. Излучение диполя. Применение электромагнитных волн................. 234

........................................................................................................................................ 413

3 ЭЛЕКТРИЧЕСТВО И ЭЛЕКТРОМАГНЕТИЗМ

Глава 11Электростатика

§ Закон Кулона

Закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q₁ и Q₂и обратно пропорциональна квадрату расстояния r между ними:

где k — коэффициент пропорциональности, зависящий от выбора системы единиц.

Сила F направлена по прямой, соединяющей взаимодействующие заряды, т. е. является центральной, и соответствует притяжению (F< 0) в случае разноименных зарядов и отталкиванию (F> 0) в случае одноименных зарядов. Эта сила называется кулоновской силой. В векторной форме закон Кулона имеет вид

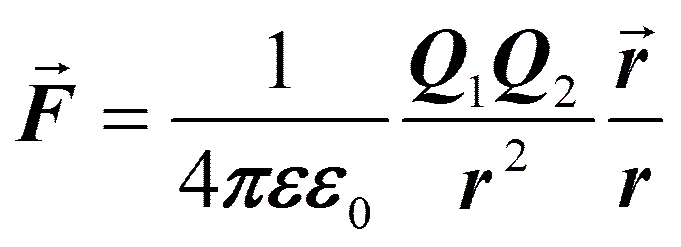
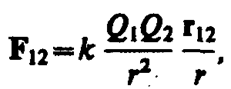(78. 1)

где F₁₂ — сила, действующая на заряд Q₁ со стороны заряда Q₂, r₁₂ — радиус-вектор, соединяющий заряд Q₂ с зарядом Q₁, r = |r₁₂| (рис. 117). На заряд Q₂ со стороны заряда Q₁ действует сила F₂₁ = –F₁₂.

В СИ коэффициент пропорциональности равен

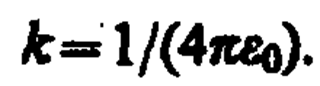
Тогда закон Кулона запишется в окончательном виде:

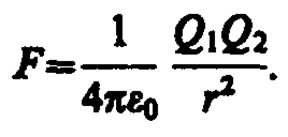(78. 2)

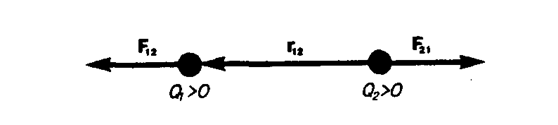
Величина e₀ называется электрической постоянной; она относится к числу фундаментальных физических постоянных и равна

(78. 3)

где фарад (Ф) — единица электрической емкости (см. § 93). Тогда

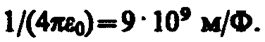
§ 79. Электростатическое поле. Напряженность электростатического поля

Если в пространство, окружающее электрический заряд, внести другой заряд, то на него будет действовать кулоновская сила; значит, в пространстве, окружающем электрические заряды, существует силовое поле. Согласно представлениям современной физики, поле реально существует и наряду с веществом является одной из форм существования материи, посредством которого осуществляются определенные взаимодействия между макроскопическими телами или частицами, входящими в состав вещества. В данном случае говорят об электрическом поле — поле, посредством которого взаимодействуют электрические заряды. Мы будем рассматривать электрические поля, которые создаются неподвижными электрическими зарядами и называются электростатическими.

Для обнаружения и опытного исследования электростатического поля используется пробный точечный положительный заряд — такой заряд, который не искажает исследуемое поле (не вызывает перераспределения зарядов, создающих поле). Если в поле, создаваемое зарядом Q, поместить пробный заряд Q₀, то на него действует сила F, различная в разных точках поля, которая, согласно закону Кулона (78. 2), пропорциональна пробному заряду Q₀. Поэтому отношение F/Q₀ не зависит от Q₀ и характеризует электростатическое поле в той точке, где пробный заряд находится. Эта величина называется напряженностью и является силовой характеристикой электростатического поля.

Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля:

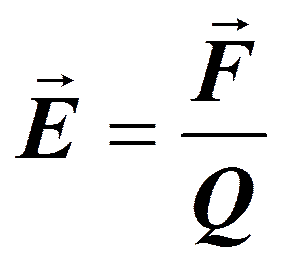
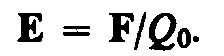(79. 1)

Как следует из формул (79. 1) и (78. 1), напряженность поля точечного заряда в вакууме

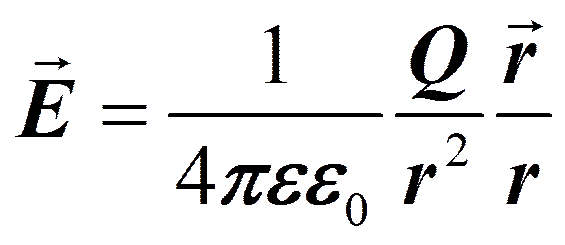
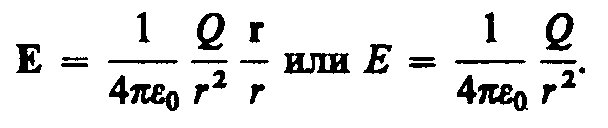(79. 2)

Направление вектора Е совпадает с направлением силы, действующей на положительный заряд. Если поле создается положительным зарядом, то вектор Е направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положительного заряда); если поле создается отрицательным зарядом, то вектор Е направлен к заряду (рис. 118).

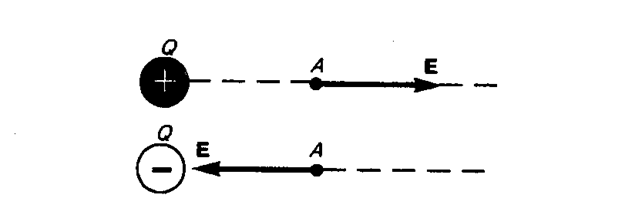
Из формулы (79. 1) следует, что единица напряженности электростатического поля — ньютон на кулон (Н/Кл): 1 Н/Кл — напряженность такого поля, которое на точечный заряд 1 Кл действует с силой в 1 Н; 1 Н/Кл= 1 В/м, где В (вольт) — единица потенциала электростатического поля (см. § 84).

Графически электростатическое поле изображают с помощью линий напряженности — линий, касательные к которым в каждой точке совпадают с направлением вектора Е (рис. 119). Линиям напряженности приписывается направление, совпадающее с направлением вектора напряженности. Так как в каждой данной точке пространства вектор напряженности имеет лишь одно направление, то линии напряженности никогда не пересекаются. Для однородного поля (когда вектор напряженности в любой точке постоянен по величине и направлению) линии напряженности параллельны вектору напряженности. Если поле создается точечным зарядом, то линии напряженности — радиальные прямые, выходящие из заряда, если он положителен (рис. 120, а), и входящие в него, если заряд отрицателен (рис. 120, б). Вследствие большой наглядности графический способ представления электростатического поля широко применяется в электротехнике.

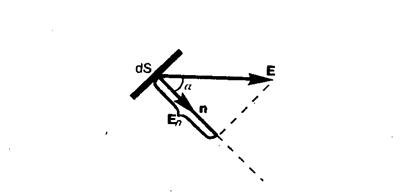
Чтобы с помощью линий напряженности можно было характеризовать не только направление, но и значение напряженности электростатического поля, условились проводить их с определенной густотой (см. рис. 119): число линий напряженности, пронизывающих единицу площади поверхности, перпендикулярную линиям напряженности, должно быть равно модулю вектора Е. Тогда число линий напряженности, пронизывающих элементарную площадку dS, нормаль n которой образует угол a с вектором Е, равно Е dS cosa = E_ndS, где Е_п—проекция вектора Е на нормаль n к площадке dS (рис. 121). Величина

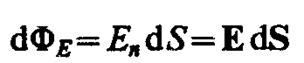
называется потоком вектора напряженности через площадку dS.

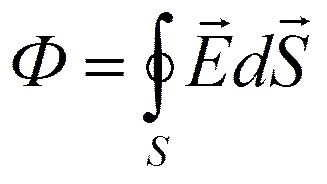
Здесь dS = dSn — вектор, модуль которого равен dS, а направление совпадает с направлением нормали n к площадке. Выбор направления вектора n (а следовательно, и dS) условен, так как его можно направить в любую сторону. Единица потока вектора напряженности электростатического поля — 1 В× м.

Для произвольной замкнутой поверхности S поток вектора Е сквозь эту поверхность

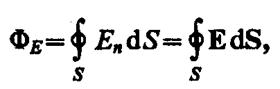(79. 3)

где интеграл берется по замкнутой поверхности S. Поток вектора Е является алгебраической величиной: зависит не только от конфигурации поля Е, но и от выбора направления n. Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т. е. нормаль, направленная наружу области, охватываемой поверхностью.

В истории развития физики имела место борьба двух теорий: дальнодействия и близкодействия. В теории дальнодействия принимается, что электрические явления определяются мгновенным взаимодействием зарядов на любых расстояниях. Согласно теории близкодействия, все электрические явления определяются изменениями полей зарядов, причем эти изменения распространяются в пространстве от точки к точке с конечной скоростью. Применительно к электростатическим полям обе теории дают одинаковые результаты, хорошо согласующиеся с опытом. Переход же к явлениям, обусловленным движением электрических зарядов, приводит к несостоятельности теории дальнодействия, поэтому современной теорией взаимодействия заряженных частиц является теория близкодействия.

§ 80. Принцип суперпозиции электростатических полей. Поле диполя

Рассмотрим метод определения модуля и направления вектора напряженности Е в каждой точке электростатического поля, создаваемого системой неподвижных зарядов Q₁, Q₂, ..., Q_n.

Опыт показывает, что к кулоновским силам применим рассмотренный в механике принцип независимости действия сил (см. § 6), т. е. результирующая сила F, действующая со стороны поля на пробный заряд Q₀, равна векторной сумме сил F_i, приложенных к нему со стороны каждого из зарядов Q_i:

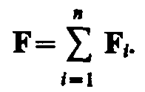(80. 1)

Согласно (79. 1), F = Q₀E и F_i = Q₀Е_i, где Е—напряженность результирующего поля, а Е_i — напряженность поля, создаваемого зарядом Q_i. Подставляя последние выражения в (80. 1), получаем

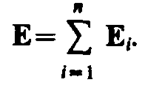(80. 2)

Формула (80. 2) выражает принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.

Принцип суперпозиции позволяет рассчитать электростатические поля любой системы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов.

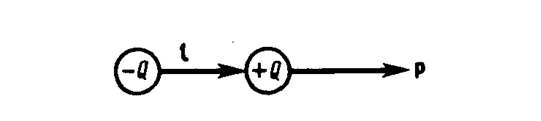
Принцип суперпозиции применим для расчета электростатического поля электрического диполя. Электрический диполь — система двух равных по модулю разноименных точечных зарядов (+Q, –Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя 1. Вектор

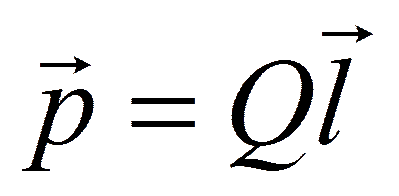
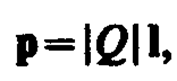(80. 3)

совпадающий по направлению с плечом диполя и равный произведению заряда |Q| на плечо l, называется электрическим моментом диполя или дипольным моментом (рис. 122).

Согласно принципу суперпозиции (80. 2), напряженность Е поля диполя в произвольной точке

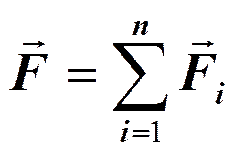
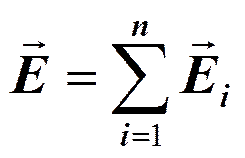
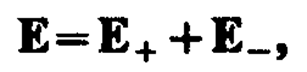
где Е₊ и Е_– — напряженности полей, создаваемых соответственно положительным и отрицательным зарядами. Воспользовавшись этой формулой, рассчитаем напряженность поля в произвольной точке на продолжении оси диполя и на перпендикуляре к середине его оси.

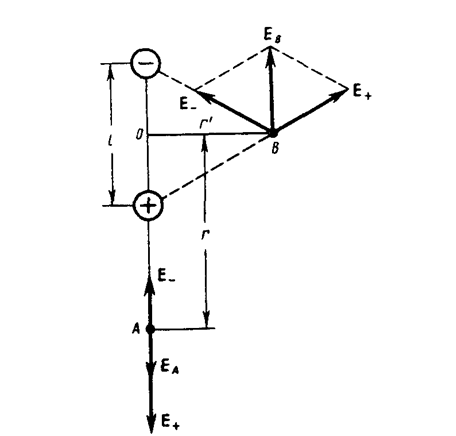
1. Напряженность поля на продолжении оси диполя в точке А (рис. 123). Как видно из рисунка, напряженность поля диполя в точке А направлена по оси диполя и по модулю равна

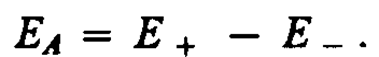
Обозначив расстояние от точки А до середины оси диполя через r, на основании формулы (79. 2) для вакуума можно записать

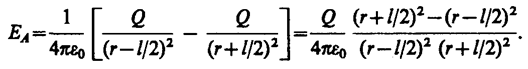
Согласно определению диполя, l/2< < r, поэтому

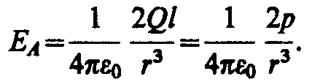
2. Напряженность поля на перпендикуляре, восставленном к оси из его середины, в точке В (рис. 123). Точка В равноудалена от зарядов, поэтому

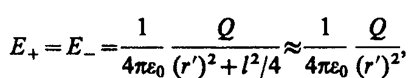(80. 4)

где r' — расстояние от точки В до середины плеча диполя. Из подобия равнобедренных треугольников, опирающихся на плечо диполя и вектор Е_B, получим

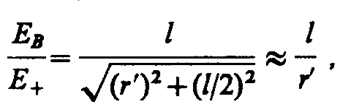
откуда

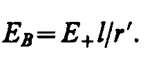(80. 5)

Подставив в выражение (80. 5) значение (80. 4), получим

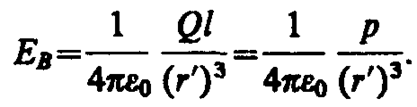
Вектор Е_B имеет направление, противоположное вектору электрического момента диполя (вектор р направлен от отрицательного заряда к положительному).

§ 81. Теорема Гаусса для электростатического поля в вакууме

Вычисление напряженности поля системы электрических зарядов с помощью принципа суперпозиции электростатических полей можно значительно упростить, используя выведенную немецким ученым К. Гауссом (1777—1855) теорему, определяющую поток вектора напряженности электрического поля сквозь произвольную замкнутую поверхность.

В соответствии с формулой (79. 3) поток вектора напряженности сквозь сферическую поверхность радиуса r, охватывающую точечный заряд Q, находящийся в ее центре (рис. 124), равен

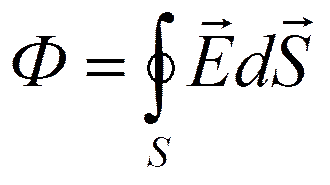
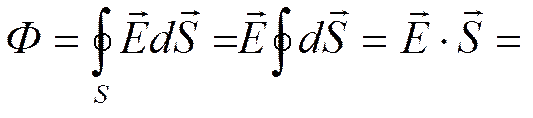
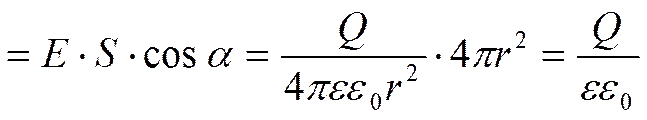
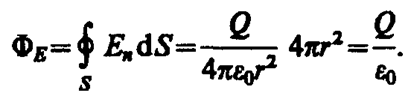
Этот результат справедлив для замкнутой поверхности любой формы. Действительно, если окружить сферу (рис. 124) произвольной замкнутой поверхностью, то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.

Если замкнутая поверхность произвольной формы охватывает заряд (рис. 125), то при пересечении любой выбранной линии напряженности с поверхностью она то входит в нее, то выходит из нее. Нечетное число пересечений при вычислении потока в конечном счете сводится к одному пересечению, так как поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линий, входящих в поверхность. Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее.

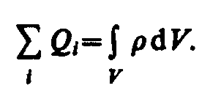(81. 3)

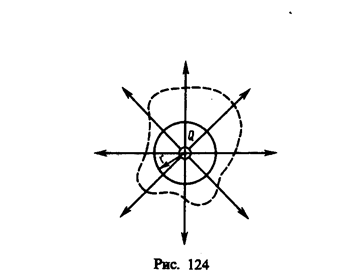
Используя формулу (81. 3), теорему Гаусса (81. 2) можно записать так:

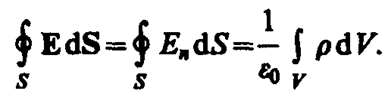
§ 82. Применение теоремы Гаусса к расчету некоторых электростатических полей в вакууме

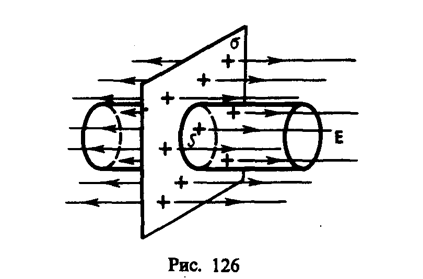
1. Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость (рис. 126) заряжена с постоянной поверхностной плотностью +s(s=dQ/dS — заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (соsa=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю,

12 3 4 5 6 7 8 9 10 Следующая ⇒

1) j2—j1 = ±2mp (т=0, 1, 2, .), тогда A=A1+A2, т. е. амплитуда результиру­ющего колебания А равна сумме амплитуд складываемых колебаний; 1 страница

1) j2—j1 = ±2mp (т=0, 1, 2, .), тогда A=A1+A2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний; 1 страница