8 вопрос: Прямоугольный треугольник. Свойства высоты и медианы, проведенных из вершины прямого угла.

8 вопрос: Прямоугольный треугольник. Свойства высоты и медианы, проведенных из вершины прямого угла.

Свойства прямоугольного треугольника:
1. Катет меньше гипотенузы.
2. Квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора): с² = а² + b².
3. Сумма острых углов прямоугольного треугольника равна 90°.
4. Медиана, проведенная к гипотенузе, равна половине гипотенузы (радиусу окружности, описанной около треугольника).

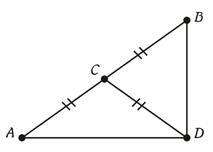
5. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
6. Если катет прямоугольного треугольника равен 1/2 гипотенузы, то угол, лежащий против этого катета, равен 30°.

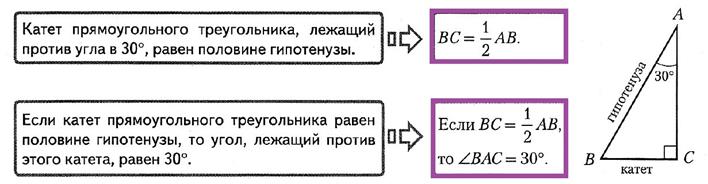
Свойство высоты, проведённой из вершины прямого угла.

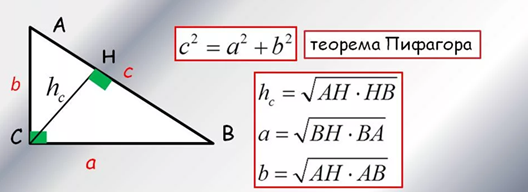
9 вопрос: Параллелограмм. Свойства и признаки параллелограмма.

10 вопрос: Квадрат. Свойства и признаки квадрата.

Свойства квадрата:
1. Квадрат имеет все свойства параллелограмма, прямоугольника и ромба.

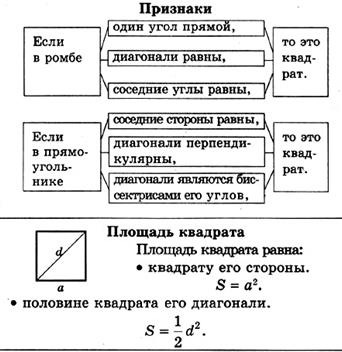
Признаки квадрата: 1. Если в ромбе один угол прямой, 2. Если в ромбе диагонали равны, 3. Если в ромбе соседние углы равны, 4. Если в прямоугольнике соседние стороны равны, 5. Если в прямоугольнике диагонали перпендикулярны, 6. Если в прямоугольнике диагонали являются биссектрисами его углов.

11 вопрос: Прямоугольник. Свойства и признаки прямоугольника.

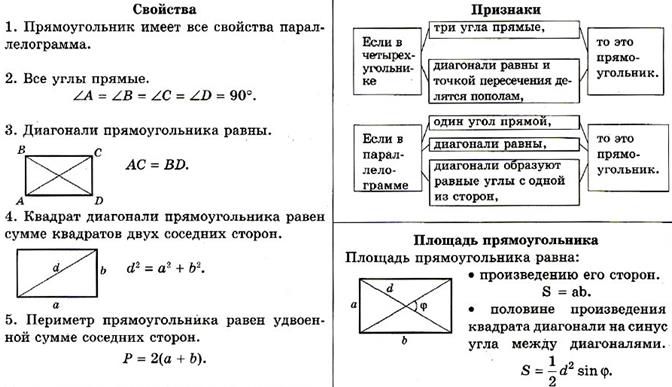
Свойства прямоугольника:
1. Прямоугольник имеет все свойства параллелограмма.
2. Все углы прямые.
3. Диагонали прямоугольника равны.
4. Квадрат диагонали прямоугольника равен сумме квадратов двух соседних сторон.
5. Периметр прямоугольника равен удвоенной сумме соседних сторон.
6. Около любого прямоугольника можно описать окружность.

Признаки прямоугольников:
Если в четырехугольнике три угла прямые.
Если в четырехугольнике диагонали равны и точкой пересечения делятся пополам.
Если в параллелограмме один угол прямой, диагонали равны.
Если в параллелограмме диагонали образуют равные углы с одной из сторон.

⇐ Предыдущая 1 234 Следующая ⇒