
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Приклади для самостійної роботи
Можна показати, що у випадку невід’ємної матриці A (aij ³ 0) існує деяке невід’ємне власне число l, яке позначимо через l(А) і відповідний йому невід’ємний власний вектор.
На основі поняття власного числа можна сформулювати умову продуктивності моделі Леонтьєва (6).
Т еорема 1. Модель Леонтьєва продуктивна тоді і тільки тоді, коли l(А)< 1.
На практиці замість сформульованої теореми користуються більш простою достатньою умовою продуктивності моделі Леонтьєва:
Т еорема 2 ( достатня умова ). Матриця A продуктивна, якщо максимум суми елементів її стовпців не перевищує одиниці, причому хоча би для одного із стовпців сума елементів строго менша за одиницю, тобто матриця A продуктивна, якщо aij ³ 0 для будь-яких (i, j=1, 2, …, n) і 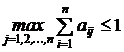 , і існує номер j такий, що
, і існує номер j такий, що 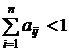 .
.
Приклад 2. В табл. 3 наведені дані про виконання балансу за звітній період в ум. гр. од. Обчислити необхідний обсяг валового випуску кожної галузі, якщо кінцеве споживання продукції енергетичної галузі (електроенергії) збільшиться удвічі, а машинобудування збережеться на попередньому рівні.
Таблиця 3
| Галузь | Споживання | Кінцевий продукт (yi) | Валовий випуск (xi) | ||
| енергетика | машинобудування | ||||
| Виробництво | Енергетика | ||||
| Машинобудування | |||||
Розв’язання. Маємо:
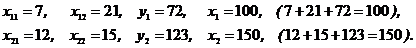
За формулами (3) знаходимо коефіцієнти прямих витрат:
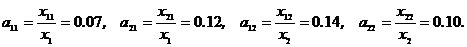
Таким чином матриця прямих витрат має вигляд
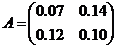 .
.
Перевіримо виконання умов продуктивності для матриці А:
1) елементи матриці невід’ємні;
2) max{0. 07+0. 12; 0. 14+0. 10 }=max{0. 19; 0. 24}=0. 24< 1.
Таким чином, на основі достатньої умови (теорема 2), робимо висновок, що матриця А продуктивна.
Примітка: Перевірку виконання умови продуктивності можна здійснити і за допомогою сформульованої вище теореми 1:
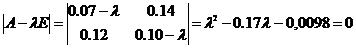
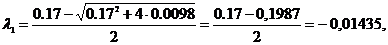
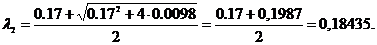
Оскільки найбільше додатне власне число 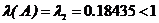 =0, то матриця А продуктивна.
=0, то матриця А продуктивна.
З продуктивності матриці випливає, що для будь-якого вектора кінцевої продукції U можна знайти необхідний обсяг валового випуску C за формулою (7).
Знайдемо матрицю повних витрат 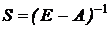 , де
, де 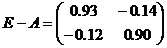 .
.
Оскільки 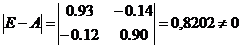 , то обернена матриця існує
, то обернена матриця існує 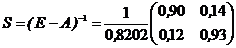 .
.
Згідно умови задачі вектор кінцевої продукції 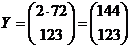 .
.
Тоді за формулою (7) одержуємо вектор валового випуску:
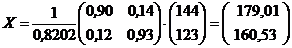 ,
,
тобто валовий випуск в енергетичній області потрібно збільшити до 179, 01 ум. од., а в машинобудівній – до 160, 53 ум. од.
Приклад 3. Підприємство складається з трьох цехів, кожен з яких виробляє один вид продукції. Прямі витрати одиниць продукції і-го цеху, що використовується (проміжний продукт) для випуску одиниці продукції j-го цеху, а також кількість одиниць продукції і-го цеху, призначених до реалізації (кінцева продукція), наведені в табл. 4.
Таблиця 4
| Продукція цехів | Прямі витрати | Кінцева продукція | ||
| 0, 2 | ||||
| 0, 2 | 0, 1 | |||
| 0, 1 | 0, 2 | |||
Визначити:
1) коефіцієнти повних витрат;
2) план (валовий випуск) кожного цеху;
3) виробничу програму цехів;
4) коефіцієнти непрямих (посередницьких) витрат.
Розв’язання. Позначимо через:
§ А – матрицю витратних коефіцієнтів, де 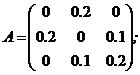
§ Х – виробничу програму підприємства, де 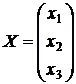 , (
, ( 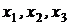 ) – плани валового випуску цехів);
) – плани валового випуску цехів);
§ Y – валовий випуск товарної продукції, де 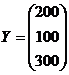 .
.
Виробничі взаємні зв’язки задовольняють співвідношення типу (5): 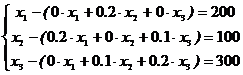 або
або 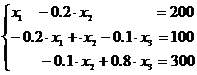 . (8)
. (8)
Ввівши позначимо Е-А=В, де Е – одинична матриця, систему лінійних алгебраїчних рівнянь (8) запишемо у вигляді
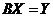 , (9) де
, (9) де
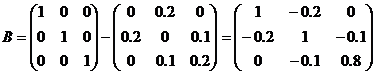 .
.
1) Коефіцієнти повних витрат – це елементи матриці 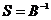 . Тому для задоволення першої вимоги поставленої задачі потрібно знайти матрицю
. Тому для задоволення першої вимоги поставленої задачі потрібно знайти матрицю 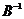 . Матриця В квадратна 3-го порядку, визначник якої
. Матриця В квадратна 3-го порядку, визначник якої
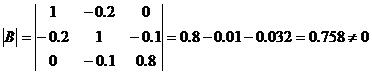 .
.
Тому 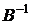 існує і систему (8) можна розв’язати матричним методом.
існує і систему (8) можна розв’язати матричним методом.
Для знаходження матриці 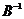 знайдемо алгебраїчні доповнення до елементів матриці В:
знайдемо алгебраїчні доповнення до елементів матриці В:
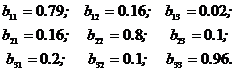
Таким чином, оберненою до В матрицею буде
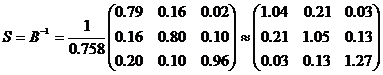 .
.
2) Знайдемо розв’язок системи (9) матричним методом:
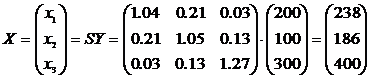
Отже, плани валового випуску продукції:
для першого цеху 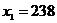 , для другого –
, для другого – 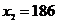 , для третього –
, для третього – 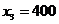 .
.
3) Визначимо виробничу програму кожного цеху, використовуючи витратні коефіцієнти 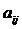 (елементи матриці А) та співвідношення
(елементи матриці А) та співвідношення 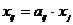 ,
,  :
:
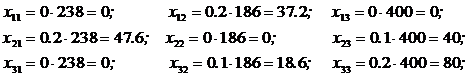
4) Коефіцієнти непрямих (посередницьких) витрат 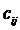 (елементи матриці С) визначаються як різниця повних внутрішньовиробничих витрат (елементи матриці
(елементи матриці С) визначаються як різниця повних внутрішньовиробничих витрат (елементи матриці 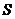 ) та прямих витрат (елементи
) та прямих витрат (елементи 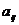 матриці А). У матричному вигляді матриця коефіцієнтів непрямих витрат буде:
матриці А). У матричному вигляді матриця коефіцієнтів непрямих витрат буде:
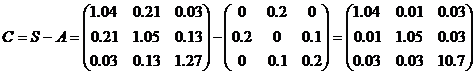 .
.
Приклади для самостійної роботи
1. У таблиці наведені дані про виконання балансу за звітний період в умовних гр. од.
Таблиця 5
| Галузь | Споживання | Кінцевий продукт | Валовий випуск | ||
| Виробництво | |||||
Обчислити необхідний обсяг валового випуску кожної галузі, якщо кінцевий продукт першої галузі повинен збільшитися вдвічі, а другої на 20%.
2. У таблиці наведені дані про виконання балансу за звітний період в умовних гр. од.
Таблиця 6
| Фірма | Споживання | Кінцевий продукт | Валовий випуск | ||
| “Альфа” | “Омега” | ||||
| Виробництво | “Альфа” | ||||
| “Омега” | |||||
Обчислити необхідний обсяг валового випуску кожної фірми, якщо:
а) кінцевий продукт фірми “Альфа” дорівнює 70, а фірми “Омега” – 120;
б) кінцевий продукт фірми “Альфа” дорівнює 60, а фірми “Омега” – 80;
3. Зв’язок “витрати-випуск” між сільським господарством і промисловістю задано технологічної матрицею (у вартісній формі) у вигляді табл. 7
Таблиця 7
| Галузь | Споживання | ||
| Сільське господарство | Промисловість | ||
| Виробництво | Сільське господарство | 0, 1 | 0, 2 |
| Промисловість | 0, 3 | 0, 5 | |
Попит (споживання) задається вектором
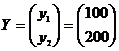 .
.
Необхідно знайти валовий випуск x=(x1, x2)T.
4. Технологічну матрицю моделі “витрати-випуск” задано у вигляді табл. 8 (в екю).
Таблиця 8
| Виробництво | Споживання | ||
| Нафта | Метал | Кам’яне вугілля | |
| Нафта | 0, 20 | 0, 10 | 0, 25 |
| Метал | 0, 15 | 0, 30 | 0, 35 |
| Кам’яне вугілля | 0, 10 | 0, 20 | 0, 25 |
Потрібно:
а) прокоментувати кожне число у другому стовпці цієї таблиці;
б) скільки необхідно матеріальних затрат (в екю) для виробництва 1 екю нафти?
в) скласти матрицю Е-А;
г) для кінцевого попиту нафти – 40, металу – 60, кам’яного вугілля – 50 скласти систему рівнянь для визначення повного (валового) випуску кожного із цих продуктів.
5. Користуючись теоремою 1 або теоремою 2, перевірити продуктивність наступних матриць:
а) 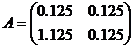 ; б)
; б) 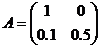 ; в)
; в) 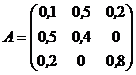 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|