Таблиця 1

Таблиця 1

Фірма	Поставки фірмі		Кінцевий продукт	Сукупний продукт
Фірма	«Альфа»	«Омега»	Кінцевий продукт	Сукупний продукт
«Альфа»
«Омега»

Кінцевий продукт (кінцевий попит)

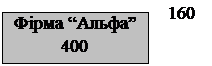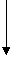
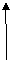
Рис. 1.

Тут стрілками позначено всі вартісні потоки, а числами величини цих потоків. Числа в прямокутниках показують сукупний продукт для кожної фірми.

Модель, розглянута вище для простого випадку двох фірм виробників, одержала назву “витрати-випуск”, або модель міжгалузевого балансу.

Далі зручно перейти до нормованих величин. Іншими словами, до витрат, віднесених до одиниці (у вартісному вираженні) продукції. Для нашого простого прикладу це можна пояснити з допомогою табл. 2.

Таблиця 2

Фірма	Поставки фірмі		Кінцевий продукт	Сукупний продукт
Фірма	«Альфа»	«Омега»	Кінцевий продукт	Сукупний продукт
«Альфа»	0, 1	0, 4
«Омега»	0, 8	0, 2

В табл. 2 перший стовпчик показує, що для виробництва одиниці продукції фірмі «Альфа» необхідні поставки від фірми «Альфа» (самій собі) в розмірі 0, 1, а від фірми «Омега» в розмірі 0, 8. Дійсно, розділивши поставки фірми «Альфа» самій собі (40) на сукупний продукт фірми «Альфа» (400), одержимо .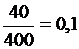

Аналогічно для поставок фірми «Омега» на одиницю продукції фірми «Альфа» .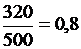

Другий стовпчик таблиці відноситься відповідно до поставок фірмі «Омега» для виробництва одиниці продукції.

Якщо опустити назви, то табл. 2 можна представити у вигляді матриці

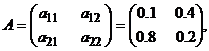
де елементи матриці 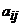називаються коефіцієнтами прямих витрат (виробничими або технологічними коефіцієнтами).

Одна із умов моделі " витрати-випуск" – лінійність зв’язків – полягає в тому, що випуск продукції передбачається пропорційний прямим витратам, тобто якщо, наприклад, ми хочемо збільшити випуск у два рази, то необхідно у два рази збільшити усі затрати.

Для нашого прикладу лінійність означає наступне.

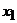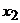Якщо позначити сукупний продукт фірми «Альфа» і фірми «Омега» через і , кінцевий продукт – через 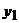і 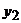відповідно, то будемо мати систему лінійних алгебраїчних рівнянь

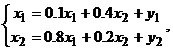
яка зв’язує виробництво на кожній фірмі одне з одним і кінцевим продуктом (попитом). Дійсно, якщо власні витрати на одиницю продукції фірми «Альфа» складають 0, 1, то для випуску 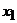продукції вони будуть 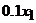(лінійність зв’язків). Відповідно, якщо фірма «Омега» на виробництво одиниці продукції здійснює закупку у фірми «Альфа» на 0, 4, то для виробництва кількості 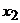ці закупки складуть 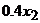. Поставки фірми «Альфа» самій собі і фірми «Омега» в сумі з кінцевим продуктом 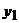якраз і складають сукупний продукт 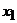. Це і є перше рівняння системи. Міркуючи аналогічно, дістанемо друге рівняння.

Цю систему рівнянь у матричних позначеннях можна записати у вигляді

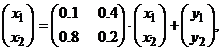
або в більш компактній формі

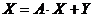, (1)

де 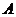– уже відома нам матриця прямих витрат, а 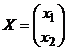і 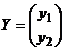– вектор стовпці сукупного і кінцевого продуктів відповідно. Рівняння (1) називають рівняння Леонтьєва.

Для прикладу розглянемо випадок двох фірм-виробників, коли сукупний продукт фірми «Альфа» дорівнює 200 ум. од., а фірми «Омега» – 300 ум. од. У цьому випадку

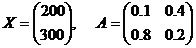
і, підставивши в рівняння, зразу знаходимо

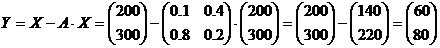Таким чином кінцевий продукт фірми «Альфа» дорівнює 60 ум. од., а фірми «Омега» – 80 ум. од.

Розглянемо більш складну, обернену задачу – визначити сукупний продукт по відомому кінцевому продукту (кінцевому попиту). Відмітимо, що саме ця задача частіше зустрічається на практиці, оскільки у ринковій економіці саме попит задає обсяг виробництва.

Знову використаємо рівняння Леонтьєва, перенісши члени, які містять Х, в ліву частину, а саме

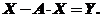
Це рівняння можна переписати у вигляді

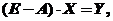
де Е – одинична матриця.

Помноживши обидві частини рівняння на матрицю (Е-А)^-1, обернену до матриці Е-А, одержимо

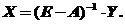
Знову розглянемо приклад з двома фірмами-виробниками. Припустимо, що кінцевий продукт фірми «Альфа» повинен складати 70 ум. од., а фірми «Омега» – 120 ум. од. Потрібно визначити необхідний сукупний продукт кожної фірми. Матриця коефіцієнтів прямих витрат А вважається заданою

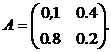
Для знаходження розв’язку знаходимо матрицю

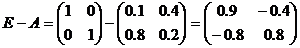
і обчислимо для неї обернену матрицю

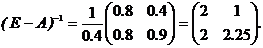
Тепер, підставляючи в формулу заданий вектор-стовпець кінцевого продукту Y, знаходимо

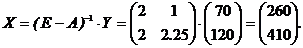
Таким чином, щоб задовольнити кінцевий попит, сукупний продукт фірми «Альфа» повинен складати 260 ум. од., а фірми «Омега» – 410 ум. од.

Або, наприклад, якщо кінцевий продукт фірми «Альфа» дорівнює 60 ум. од., а фірми «Омега» – 80 ум. од., тобто

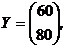
то використавши раніше знайдену матрицю (Е-А) ^-1, легко знаходимо

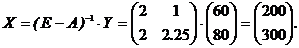
Таким чином, для задоволення останнього варіанту кінцевого попиту сукупний продукт фірми «Альфа» повинен бути 200 ум. од., а фірми «Омега» – 300 ум. од.

Перейдемо до узагальнення і уточнення моделі Леонтьева.

Основні припущення моделі міжгалузевого балансу або моделі Леонтьєва, зводяться до наступного:

1. В економічній системі виробляється, продається, купується, споживається і інвестується n видів продукції.

2. Кожна галузь є “чистою”, тобто виробляє лише один вид продукції, спільне виробництво різної продукції виключається. Різні галузі виробляють різну продукцію, і тому галузь, що виробляє продукцію виду i, будемо позначати тим самим індексом.

3. Під виробничим процесом у кожній галузі будемо розуміти перетворення деяких (можливо, всіх) видів продукції, взятих у певних кількостях, у деяку кількість продукції одного чи іншого виду. При цьому припускається, що співвідношення затраченої і випущеної продукції є сталим. Таким чином, якщо для виробництва одиниці продукції в j-й галузі треба витратити a_ij одиниць i-ї продукції, то випуск λ одиниць j-ї продукції потребує витрат λ a_ij одиниць i-ї продукції.

Розглянемо процес виробництва за деякий період часу (наприклад, рік).

Введемо наступні позначення:

§ x_i – загальний (валовий) обсяг продукції, випущеної галуззю під номером і (і=1, 2, …. n);

§ x_ij – обсяг продукції i-ї галузі, яка споживається j-ю галуззю в процесі виробництва (і, j=1, 2, …. n);

§ y_i – обсяг кінцевої продукції i-ї галузі для невиробничого використання.

Оскільки валовий обсяг продукції будь-якої i-ї галузі дорівнює сумарному обсягу продукції, яка споживається n галузями, і кінцевого продукту, то

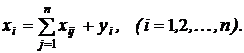(2)

Рівняння (2) називаються співвідношеннями балансу. Будемо розглядати вартісний міжгалузевий баланс, коли всі величини, які входять в (2) мають вартісне вираження.

Введемо коефіцієнти прямих витрат

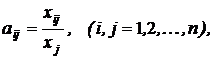(3)

які показують витрати продукції i-ї галузі на виробництво одиниці продукції j-ї галузі. При i=j маємо витрати власної продукції галузі на одиницю її валового обсягу.

Можна вважати, що на протязі деякого проміжку часу коефіцієнти a_ij будуть постійними і залежними лише від технології виробництва. Це означає лінійну залежність матеріальних витрат від валового випуску, тобто

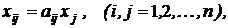(4) внаслідок чого побудована на такому припущенні модель міжгалузевого балансу одержала назву лінійної.

Тепер співвідношення балансу (2) набудуть вигляду

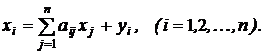(5)

Введемо позначення:

, , ,

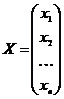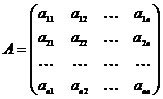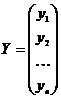де Х – вектор валового випуску, Y – вектор кінцевої продукції, А – матриця прямих витрат, яку часто називають технологічною матрицею, а коефіцієнти a_ij – технологічними коефіцієнтами.

Тоді систему (5) можна записати у матричному вигляді

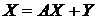(6)

або

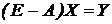, (6’)

де через Е позначено одиничну матрицю.

Система рівнянь (5), (6) або (6’) є основним інструментом аналізу міжгалузевих зв’язків, методу, що дістав назву метод “витрати-випуск”, або метод Леонтьєва.

Таким чином, основна задача міжгалузевого балансу полягає в знаходженні такого вектора валового випуску Х, який при відомій матриці прямих витрат А забезпечує заданий вектор кінцевої продукції Y.

Якщо матриця (Е-А) невироджена, тобто |Е-А| ¹ 0, то згідно матричного методу

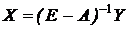. (7)

Матриця 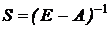називається матрицею повних витрат.

Щоб з’ясувати економічний зміст елементів матриці S, будемо задаватися кінцевим продуктом у вигляді одиничних векторів:

, , .

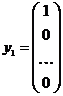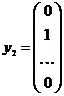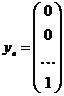Тоді з огляду на те, що 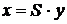, відповідні вектори валового випуску будуть:

, , .

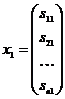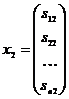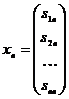Отже, кожний елемент 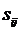матриці S є величина валового випуску продукції i-ї галузі, необхідного для забезпечення випуску одиниці кінцевої продукції j-й галузі y_j=1 (j=1, 2, …, n).

У відповідності з економічним змістом задачі значення x_i повинні бути невід’ємні (x_i ³ 0) при невід’ємних значеннях y_j (y_j ³ 0) і a_ij ³ 0, де (i, j=1, 2, …, n).

Матриця A, елементи якої задовольняють умову a_ij ³ 0, називається продуктивною, якщо для будь-якого вектора Y (y_j ³ 0) існує розв’язок X (x_i ³ 0) рівняння (6’). У цьому випадку і модель Леонтьєва називається продуктивною.

Існує декілька критеріїв продуктивності матриці A. Один із них пов’язаний поняттям власного числа матриці A.

Нагадаємо, що число l, що задовольняє рівняння 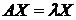, називають власним числом або власним значенням матриці A, а вектор X – власним вектором, що відповідає власному числу l.

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒