Хелпикс

Главная

Контакты

Случайная статья



В)В.Гейзенберг. С)Э.Шредингер. А) матрицалық элемент. E) диагональдық матрица. C) ауысулардың мүмкін болатындығын, не мүмкін еместігін. D)күй векторы.  A) матрицалық көріністе шешу

⇐ ПредыдущаяСтр 14 из 16Следующая ⇒


В)В. Гейзенберг

С)Э. Шредингер

D)М. Планк

E)А. Эйнштейн

2. Кванттық теорияның «Толқ ындық » тұ жырымдамасын дамытқ ан ғ алым?

А)П. Дирак

В)В. Гейзенберг

С)Э. Шредингер

D)М. Планк

E)А. Эйнштейн

3. 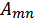=  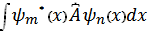, мұ ндағ ы  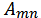дегеніміз не?

А) матрицалық элемент

В) кө бейту операторы

     С) қ осу операторы

D) орташа мә ні

E)кет векторы

4. 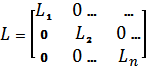, мұ ндағ ы 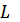дегеніміз?

A) кет векторы

B) қ осу операторы

C)матрицалық элемент

D) кө бейту операторы

E) диагональдық матрица

5. Сұ рыптау ережелері нені кө рсетеді?

A)ауысулардың тек мү мкін болатындығ ын

B) ауысулардың тек мү мкін еместігін

C) ауысулардың мү мкін болатындығ ын, не мү мкін еместігін

D) радиус-векторлардың матрицалық элементі нө льге тең дігін

E) радиус-векторлардың матрицалық элементі тек бү тін санғ а тең дігін

6. Кванттық жү йенің кү йін сипаттайтын толқ ындық функцияны Гильберт кең істігінде қ андай вектор ретінде қ арастыруғ а болады?

A) толқ ындық вектор

B) жылдамдық векторы

C) радиус-вектор

D)кү й векторы

 E)кү ш векторы

7. “Кет”-векторлары қ алай белгіленеді?

A) |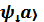  

B) < ψ а ψ а>

 C)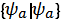

D)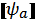

E) (ψ а ψ а)

8. “Бра”-векторлары қ алай белгіленеді?

A)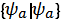

B)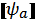

C)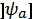

D)⟨ |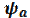

 E)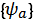

9. Қ андай ә діс арқ ылы екінші ретті дифференциалдық тең деу болып табылатын Шредингер тең деуін бірінші ретті біртекті сызық ты алгебралық тең деулер жү йесіне келтіруге болады?

 A) матрицалық кө ріністе шешу

B) унитарлы кө ріністе шешу

C) кең істік бойынша интегралдау арқ ылы шешу

D) сұ рыптау арқ ылы шешу

E) векторлық кө ріністе шешу

10. Кванттық жү йені кү й векторлары арқ ылы сипаттауды ұ сынғ ан ағ ылшын ғ алымы?


⇐ Предыдущая78910111213141516Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.