
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
А. Импульстың сақталу заңы
А. Импульстың сақ талу заң ы
В. Энергияның сақ талу заң ы
С. Ньютонның екінші заң ы
D. Масса мен энергияның ө зара байланыс заң ы
Е. Стефан-Больцман заң ы
- Фотоэффект ү шін Эйнштейн
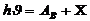 тең деуінде Х таң басымен белгіленген........ .
тең деуінде Х таң басымен белгіленген........ .
А. Фото электрондардың максимал кинетикалық энергиясы;
В. Фото электро массасы;
С. Фото электрондардың максимал жылдамдығ ы;
D. Тү скен фотон энергиясы;
Е. Жабатын потенциал.
- Келтiрiлген формулалардың қ айсысы фотоэффект ү шiн Эйнштейн тең деуiн сипаттайды?
- e=hn;
- hn=A;
- hn=A+ mV2/2;
- eU= mV2/2;
- w=2pn;
49. Тө мендегi келтiрiлген тең деулердiң қ айсысы фотоэффектiң негiзгi заң дылық тарын сипаттайды?
А. hn = AВ+ mV2/2;
В. e = hn;
С. Dl=h(1-cosθ )/(m0c);
D. Еn = (n +1/2)ћw;
E. р=w(1+r);
50. Фотоэффектінің қ ызыл шекарасы анық талатын формула: А. hn = AВ+ mV2/2;
B) hn = AВ C) hn =ε D) A = mV2/2 E) A = mc2
Комптон эффектiсi
51. Комптон эффектiсi деген не?
А. Мө лдір емес ортада жарық тың шашырауы;
В. Рентген сә улелерiнiң дифракциясы;
С. Электрондардан шашырағ анда рентген сә улелерiнiң толқ ын ұ зындық тарының ө згеруi;
D. Жарық кванттарының заттан электрондарды шығ аруы;
Е. Қ ызғ ан денелердiң электромагниттiк толқ ындар шығ аруы;
- Еркін электрондардан комптондық шашырау кезінде толқ ын ұ зындығ ының минимал ө згерісі....... тең.
А. 5, 68пм;
В. 4, 84пм;
С. 0;
D. 4, 42пм;
Е. 11, 36пм;
| № п/п | Вопрос | Ответ №1 | Ответ №2 | Ответ №3 | Ответ №4 | Ответ №5 |
| 1. | 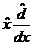 - операторының cos x функциясына ә серін анық таң ыз - операторының cos x функциясына ә серін анық таң ыз
| –х sin x | sin x | х sin x | х cos x | 2х cos x |
| 2. | 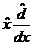 - операторының sin x функциясына ә серін анық таң ыз - операторының sin x функциясына ә серін анық таң ыз
| –х sin x | sin x | х sin x | х cos x | 2х cos x |
| 3. | 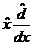 - операторының - операторының 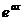 функциясына ә серін анық таң ыз функциясына ә серін анық таң ыз
| 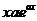
| 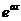
| 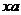
| 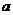
| 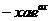
|
| 4. | 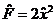 операторының операторының 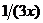 функциясына ә серін анық таң ыз функциясына ә серін анық таң ыз
| 
| 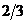
| 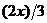
| 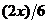
| 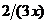
|
| 5. | 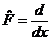 операторының операторының 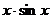 функциясына ә серін анық таң ыз функциясына ә серін анық таң ыз
| 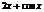
| 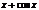
| 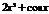
| 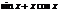
| 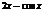
|
| 6. | 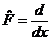 операторының операторының 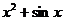 функциясына ә серін анық таң ыз функциясына ә серін анық таң ыз
| 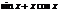
| 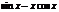
| 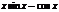
| 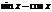
| 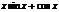
|
| 7. | Берілген 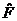 жә не жә не 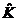 операторларының қ осындысының операторларының қ осындысының 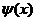 функциясына ә серін анық таң ыз, мұ ндағ ы: функциясына ә серін анық таң ыз, мұ ндағ ы:
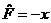 , , 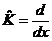 , , 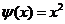 ; ;
| 2 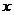
| 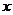
| 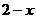
| 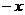
| 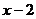
|
| 8. | Берілген 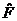 жә не жә не 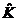 операторларының қ осындысының операторларының қ осындысының 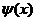 функциясына ә серін анық таң ыз, мұ ндағ ы: функциясына ә серін анық таң ыз, мұ ндағ ы:
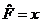 , , 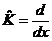 , , 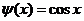 ; ;
| 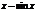
| 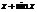
| 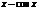
| 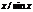
| 
|
| 9. | Берілген 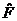 жә не жә не 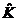 операторларының қ осындысының операторларының қ осындысының 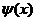 функциясына ә серін анық таң ыз, мұ ндағ ы: функциясына ә серін анық таң ыз, мұ ндағ ы:
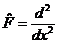 , , 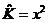 , , 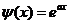 ; ;
| 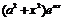
| 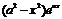
| 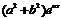
| 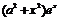
| 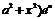
|
| 10. | Берілген 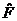 жә не жә не 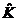 операторларының айырымының операторларының айырымының 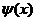 функциясына ә серін анық таң ыз, мұ ндағ ы: функциясына ә серін анық таң ыз, мұ ндағ ы:
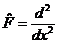 , , 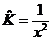 , , 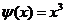 ; ;
| 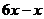
| 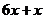
| 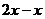
| 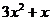
| 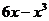
|
| 11. | Берілген 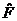 жә не жә не 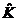 операторларының кө бейтіндісінің операторларының кө бейтіндісінің 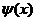 функциясына ә серін анық таң ыз, мұ ндағ ы: функциясына ә серін анық таң ыз, мұ ндағ ы:
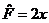 , , 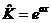 , , 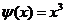 ; ;
| 
| 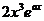
| 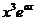
| 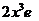
| 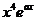
|
| 12. | Берілген 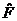 жә не жә не 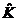 операторларының кө бейтіндісін анық таң ыз, мұ ндағ ы: операторларының кө бейтіндісін анық таң ыз, мұ ндағ ы:
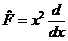 , , 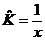 ; ;
| 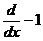
| 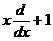
| 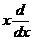
| 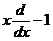
| |
| 13. | Берілген 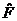 жә не жә не 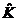 операторларының кө бейтіндісін анық таң ыз, мұ ндағ ы: операторларының кө бейтіндісін анық таң ыз, мұ ндағ ы:
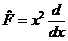 , , 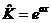 ; ;
| 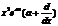
| 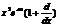
| 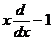
| 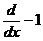
| 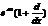
|
| 14. | Берілген 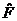 жә не жә не 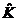 операторларының кө бейтіндісін анық таң ыз, мұ ндағ ы: операторларының кө бейтіндісін анық таң ыз, мұ ндағ ы:
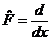 , , 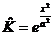 ; ;
| 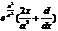
| 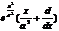
| 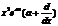
| 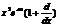
| 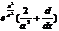
|
| 15. | Берілген 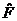 жә не жә не 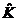 операторларының кө бейтіндісін анық таң ыз, мұ ндағ ы: операторларының кө бейтіндісін анық таң ыз, мұ ндағ ы:
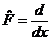 , , 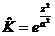 ; ;
| 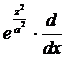
| 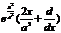
| 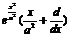
| 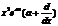
| 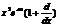
|
| 16. | Берілген 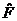 жә не жә не 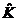 операторларының комутаторын анық таң ыз, мұ ндағ ы: операторларының комутаторын анық таң ыз, мұ ндағ ы:
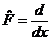 , , 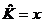 ; ;
| x | x2 | |||
| 17. | Берілген 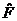 жә не жә не 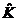 операторларының комутаторын анық таң ыз, мұ ндағ ы: операторларының комутаторын анық таң ыз, мұ ндағ ы:
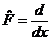 , , 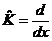 ; ;
| x | x2 | 2x | ||
| 18. | Берілген 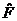 жә не жә не 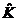 операторларының комутаторын анық таң ыз, мұ ндағ ы: операторларының комутаторын анық таң ыз, мұ ндағ ы:
 , , 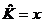 ; ;
| x | y | |||
| 19. | Ә сер ететін функцияғ а кө бейту операторының дұ рыс ө рнегін кө рсет: | 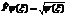
| 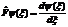
| 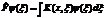
| 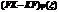
| 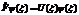
|
| 20. | Ә сер ететін функцияның квадрат тү бірін табу операторының дұ рыс ө рнегін кө рсет: | 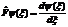
| 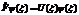
| 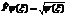
| 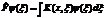
| 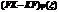
|
| 21. | Ә сер ететін функцияны дифференциалдау операторының дұ рыс ө рнегін кө рсет: | 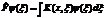
| 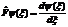
| 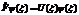
| 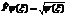
| 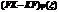
|
| 22. | Ә сер ететін функцияны интегралдау операторының дұ рыс ө рнегін кө рсет: | 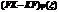
| 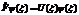
| 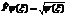
| 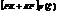
| 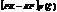
|
| 23. | Екі оператор комутаторының дұ рыс ө рнегін кө рсет: | 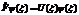
| 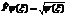
| 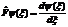
| 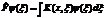
| 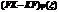
|
| 24. | Операторлардың қ осындысының жә не айырымының дұ рыс ережесін кө рсет: | 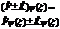
| 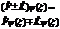
| 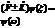
| 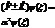
| 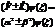
|
| 25. | Берілген 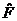 оператордың оператордың 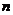 дә режесі деп..... дә режесі деп.....
| 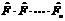
| 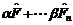
| 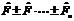
| 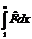
| 
|
| 26. | 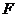 физикалық шаманың физикалық шаманың 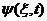 кванттық кү йіндегі орташа мә нін анық тайтын дұ рыс ө рнегін кө рсет: кванттық кү йіндегі орташа мә нін анық тайтын дұ рыс ө рнегін кө рсет:
| 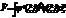
| 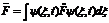
| 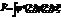
| 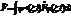
| 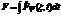
|
| 27. | Толық энергияғ а сә йкес келетін опратордың дұ рыс ө рнегін кө рсет: | 
| 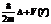
| 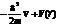
| 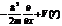
| 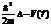
|
| 28. | Импульс мометінің OX осіне тү сірілген қ ұ раушысының операторын анық тайтын дұ рыс орнекті кө рсет: | 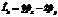
| 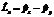
| 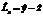
| 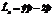
| 
|
| 29. | Импульс мометінің OY осіне тү сірілген қ ұ раушысының операторын анық тайтын дұ рыс орнекті кө рсет: | 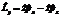
| 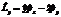
| 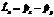
| 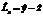
| 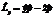
|
| 30. | Импульс мометінің OZ осіне тү сірілген қ ұ раушысының операторын анық тайтын дұ рыс орнекті кө рсет: | 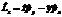
| 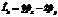
| 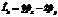
| 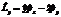
| 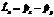
|
| 31. | Импульс мометінің квадратының операторын анық тайтын дұ рыс орнекті кө рсет: | 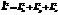
| 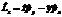
| 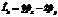
| 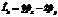
| 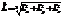
|
| 32. | Оператордың ө зіндік функциясының бар болуының, қ андай шартымен қ анағ аттандырылуы керек: 1. бірмә нділік шартымен 2. шектілік шартымен 3. ү здіксіздік шартымен | 1-3 | 2-3 | 1, 3 | ||
| 33. | 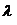 мә нінің мә нінің 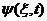 кү йінде анық талу шартының дұ рыс ө рнегін кө рсет: кү йінде анық талу шартының дұ рыс ө рнегін кө рсет:
| 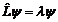
| 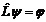
| 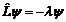
| 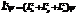
| 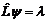
|
| 34. | Нормалау шартының дұ рыс ө рнегін кө рсет | 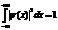
| 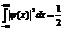
| 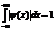
| 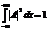
| 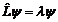
|
| 35. | Бірө лшемді, тікбұ рышты, шексіз терең, потенциалдық шұ ң қ ырдың потенциалдық энергиясы қ андай шартты қ анағ аттандыру керек: | 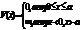
| 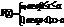
| 
| 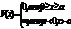
| Бірмә нділік, шектілік, ү здіксіздік шарттарын қ анағ аттандыру керек. |
| 36. | Бірө лшемді, тікбұ рышты, шексіз терең, потенциалдық шұ ң қ ырдағ ы шешімінің толық шешімін кандай тү рде іздейміз: | 
| 
| 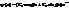
| 
| 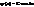
|
| 37. | Бірө лшемді, тікбұ рышты, шексіз терең, потенциалдық шұ ң қ ырдағ ы нормаланбағ ан шешімін дұ рыс ө рнегін кө рсет: | 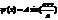
| 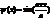
| 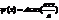
| 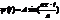
| 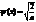
|
| 38. | Бірө лшемді, тікбұ рышты, шексіз терең, потенциалдық шұ ң қ ырдағ ы нормаланғ ан шешімін дұ рыс ө рнегін кө рсет: | 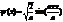
| 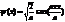
| 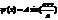
| 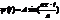
| 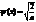
|
| 39. | Тө мендегі қ андай шарт орындалғ анда берілген 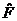 операторының эрмитті тү йә ндесі операторының эрмитті тү йә ндесі 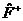 оператор деп айтамыз: оператор деп айтамыз:
| 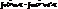
| 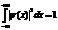
| 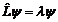
| 
| 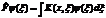
|
| 40. | 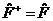 шарты қ андай операторды анық тайды: шарты қ андай операторды анық тайды:
| Эрмитті операторды | Транспонирленген операторды | Комплекісті тү йіндес операторды | Сызық ты операторды | Унитарлы операторды |
1. Неміс ғ алымы В. Гейзенберг қ ай жылы кванттық теориядағ ы проблемаларды шешіп, қ исынды жү йе ұ сынды?
a. 1930
b. 1934
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|