
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Б) Ly= iħ(Px -Pz ). Б) Импульс операторының координаттық көрінісі. С) = =(2πħ)-3/2exp(ipr∕ħ)
Б) Ly= iħ (Px -Pz )
C) P
Д) -iħ 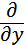
E) iħ 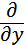
5. -iħ 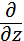 ө рнегі қ ай кө ріністің операторы:
ө рнегі қ ай кө ріністің операторы:
А) Координат операторының импульстық кө рінісі
Б) Импульс операторының координаттық кө рінісі
С) Импульс моментінің координаттық кө рінісі
Д) Кинетикалық энергияның импульс кө ріністегі ө рнегі
Е) Координат операторының координаттық кө ріністегі ө рнегі
6. Импульс моментінің импульстық кө ріністегі ө рнегі:
А) iħ 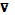 p
p
Б) iħ [ 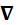 p× p]
p× p]
С) iħ 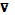 r
r
Д) P
Е) 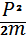
7. Импульс операторының координаттық кө ріністегі ө зіндік функциясы
А) 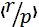 =
= 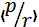
Б) 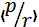 =
= 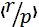
С) = =(2π ħ )-3/2exp(ipr∕ ħ )
Д) 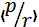 =
= 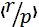 =(2π ħ )-3/2exp(irp∕ ħ )
=(2π ħ )-3/2exp(irp∕ ħ )
Е) 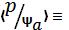 a(P)
a(P)
8. Импульстық кө ріністегі толқ ындық функция неге тең
А)  F(l)
F(l) 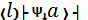
Б) P·a(P)· 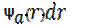
С) r(P)· a(P) 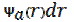
Д) 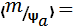 F(m)
F(m) 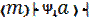
Е) a(P)
9. Кинетикалық энергияның координаттық кө ріністегі ө рнегі:
А) 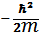
Б) 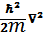
С) 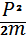
Д) - 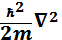
Е) 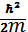
10. Импульс операторының импульстық кө ріністегі ө рнегі
А) P, Px, Py, Pz
Б) iħ [ 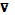 p× p]
p× p]
С) 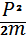
Д) iħ 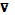 p
p
Е) iħ 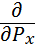 iħ
iħ 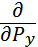 iħ
iħ 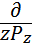
| № | Сұ рақ тар | А | В | С | Д | Е |
| 1. | Бұ рыштық моментінің декарттық координаттар жү йесіне қ андай кванттық операторлар сә йкес қ ойылады? | 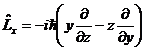 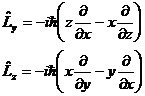 
| 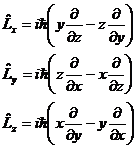
| 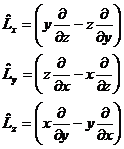
| 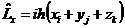
| Бұ рыштыұ моментін декарттық координаттар жү йесіне сә кес қ оюғ а болмайды |
| 2. | Бұ рыштық моментінің дұ рыс жазылғ ан координаттармен ауыстырымдылық қ атынасын кө рсет |
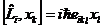
|
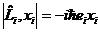
|
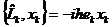
|
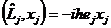
| Барлық нұ сқ алар дұ рыс |
| 3. | 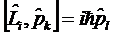 -қ андай тендеу? -қ андай тендеу?
| Импульс пен бұ рыштық момент операторларының коммутаторлық тең деуі | Импульс пен бұ рыштық момент арасындағ ы байланыс тең деуі | Бұ рыштық момент пен импульс моментінің байланыс тең деуі | Бұ рыштық моменті мен импульс моментінің тә уелділік тең деуі | Бұ рыштық моменті мен импульстің тә уелділік тең деуі |
| 4. | Бұ рыштық момент проекциялары ө зара қ алай коммутацияланады? | 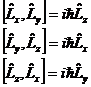
| 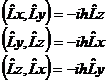
| 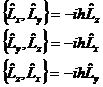
| 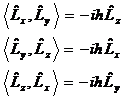
| Бұ рыштық момент проекциялары коммутацияланбайды |
| 5. | 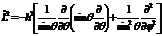
| Бұ рыштық моментінің квадраттық операторының ө рнегі | Бұ рыштық моментінің ө рнегі | Бұ рыштық моментінің коммутаторлық ө рнегі | Импульс моментінің ө рнегі | Импульс моментінің квадраттық ө рнегі |
| 6. | Магниттік кванттық санды қ андай ә ріппен белгілейміз? | m | n | 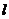
| s | k |
| 7. | Спиндік кванттық санды қ алай белгілейміз? | s | m | n | 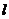
| k |
| 8. | Қ озғ алыс мө лшері моментінің кванттық саны | j | m | n | k | S |
| 9. | Орбиталық кванттық сан | 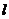 
| M | n | s | J |
| 10. | Спиндік функция тең деуі: | 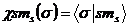
| 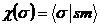
| 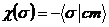
| 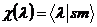
| 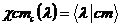
|
| 11. | Спиндік толқ ынды функцияның екінші атауы | Спинорлар | минорлар | детекторлар | дуплет | Тритерийлер |
| 12. | 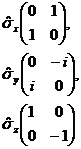 Кімнің матрицалары
Кімнің матрицалары
| Паули матрицалары | Гейзенберг матрицасы | Дирак матрицасы | Шредингер матрицасы | Максвелл матрицасы |
| 13. | Паули матрицаларының қ асиеттерін анық та | Эрмитті, унитарлы | Эрмитті емес, унитарлы | Нақ ты, унитарлы | Ү здіксіздік, унитарлы | Ү здікті, эрмитті |
| 14. | 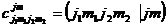 Кімнің коэффициенті? Кімнің коэффициенті?
| Клебш - Гордан | Паули | Гейзенберг | Дирак | Максвелл |
| 15. | 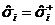 қ андай матрицасы? қ андай матрицасы?
| Паули матрицасының эрмитті тү рі | Паули матрицасының унитарлы тү рі | Дирак матрицасының ү здікті тү рі | Клебш-Гордан матрицасының нақ ты тү рі | Гейзенберг матрицасы |
| 16. | Егер ү шбұ рыштар ережесі орындалмаса, онда векторлық қ осу коэффициенті | Нө лге тең болады | Бірге тең болады | Екіге тең болады | Бір – бірінен тә уелсіз | Анық талмайды |
| 17. | Клебш – Гордан коэффициентінің орнына | Вингердің 3j- символарын қ олданады | Паули символы қ олданылады | Паулидің 2 j- символы қ олданылады | Паулидің 2i- символы қ олданылады | Паулидің 2k- символы қ олданылады |
| 18. | Векторлық қ осу коэффициентінің қ асиетін кө рсет | симметриялық | ү здіксіздік | ү здікті | Бірмә нділік | Шексіздік |
| 19. | 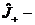 қ андай оператор? қ андай оператор?
| жоғ арылатқ ыш | Тө мендеткіш | Дә режелік | сипаттаушы | теріс |
| 20. | 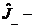 қ андай оператор? қ андай оператор?
| Тө мендеткіш | жоғ арылатқ ыш | Дә режелік | сипаттаушы | теріс |
1. Кванттық теорияның «Матрицалық » тұ жырымдамасын 1925 жылы енгізген ғ алым?
А)П. Дирак
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|