
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Полярная система координат. Арифметические операции над комплексными числами
Полярная система координат
Полярная система координат на плоскости задается точкой  , которая называется полюсом, и лучом, который называется полярной осью. Координатами точки в полярной системе координат являются расстояние точки от полюса
, которая называется полюсом, и лучом, который называется полярной осью. Координатами точки в полярной системе координат являются расстояние точки от полюса  и угол
и угол  между полярной осью и радиус-вектором этой точки. Этот угол называется полярным углом.
между полярной осью и радиус-вектором этой точки. Этот угол называется полярным углом.
Можно установить связь между полярной системой координат и декартовой прямоугольной системой, если поместить начало декартовой прямоугольной системы в полюс, а полярную ось направить вдоль положительного направления оси  :
:

Из геометрических соображений видно, что координаты точки  в декартовой и полярной системах координат связываются соотношениями:
в декартовой и полярной системах координат связываются соотношениями:  ;
;  ;
;  ;
;  . Тогда комплексное число
. Тогда комплексное число 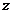 можно переписать в виде:
можно переписать в виде:  .
.
Такая форма записи называется тригонометрической формой записи комплексного числа. При этом величина  называется модулем комплексного числа, а угол наклона
называется модулем комплексного числа, а угол наклона  - аргументом комплексного числа.
- аргументом комплексного числа.
Очевидно, что комплексно-сопряженные числа имеют одинаковые модули и противоположные аргументы.
Арифметические операции над комплексными числами
Пусть  ,
,  или в тригонометрической форме
или в тригонометрической форме  ,
,
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|