Комплексные числа

Определение Комплексным числом 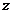называется выражение , где и – действительные числа, – мнимая единица. При этом называется действительной частью числ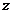а ( ), а - мнимой частью числа ( ).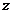

Если , то число будет чисто мнимым, если , то число будет действительным.

Определение Числа и называются комплексно-сопряженными.

Определение Два комплексных числа и называются равными, если соответственно равны их действительные и мнимые части: .

Определение Комплексное число равно нулю, если равны нулю его действительная и мнимая части:

Понятие комплексного числа имеет геометрическую интерпретацию. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью. Таким образом, на оси располагаются действительные числа, а на оси – чисто мнимые.

12 3 Следующая ⇒