Глава XXIII. Описание меридианов и параллелей, помещаемых на изображении земли

Крайние меридианы, как было доказано выше, охватывают 12 часовых промежутков. Крайняя же южная параллель находится от экватора на таком расстоянии, на каком к северу от него лежит параллель, проходящая через Мероэ. Мы, однако, нашли уместным проводить меридианы через каждую треть часового промежутка по экватору, то есть через каждые 5 принятых нами делений экватора. Что же касается параллелей, лежащих к северу от экватора, то их мы проведем так, чтобы:
первая параллель была короче его на ¹/₄ часового промежутка и отстояла по меридиану, как следует из геометрических расчетов, приблизительно на 4¹/₄ градуса;
вторая параллель была короче на ¹/₂ часового промежутка и отстояла соответственно на 8⁵/₁₂ градуса;
третья параллель была короче на ¹/₄ часового промежутка и отстояла на 12¹/₂ градуса;
четвертая параллель была короче на 1 часовой промежуток, отстояла на 16⁵/₁₂ градуса и проходила через Мероэ;
пятая параллель была короче на 1¹/₄ часового промежутка и отстояла на 20¹/₄ градуса;
шестая параллель, идущая по летнему тропику, была короче на 1¹/₂ часовых промежутка и отстояла на 23⁵/₆ градуса, проходя через Сиену;
седьмая параллель была короче на 1³/₄ часового промежутка и отстояла на 27¹/₆ градуса;
восьмая параллель была короче на 2 часовых промежутка и отстояла на 30¹/₃ градуса;
девятая параллель была короче на 2¹/₄ часовых промежутка и отстояла на 33¹/₃ градуса;
десятая параллель была короче на 2¹/₂часовых промежутка, отстояла на 36 градусов и проходила через Родос;
одиннадцатая параллель была короче на 2³/₄часового промежутка и отстояла на 38¹/₇ градуса;
двенадцатая параллель была короче на 3 часовых промежутка и отстояла на 40¹¹/₁₂ градуса;
тринадцатая параллель была короче на 3¹/₄ часовых промежутка и отстояла на 43¹/₁₂ градуса;
четырнадцатая параллель была короче на 3¹/₂ часовых промежутка и отстояла на 45 градусов;
пятнадцатая параллель была короче на 4 часовых промежутка и отстояла на 48¹/₂ градусов;
шестнадцатая параллель была короче на 4¹/₂ часовых промежутка и отстояла на 51¹/₂ градуса;
семнадцатая параллель была короче на 5 часовых промежутков и отстояла на 54 градуса;
восемнадцатая параллель была короче на 5¹/₆часовых промежутка и отстояла на 56¹/₆ градуса;
девятнадцатая параллель была короче на 6 часовых промежутков и отстояла на 58 градусов;
двадцатая параллель была короче на 7 часовых промежутков и отстояла на 61 градус;
двадцать первая параллель была короче на 8 часовых промежутков, отстояла на 63 градуса и проходила через Фуле. Кроме того, будет проведена еще параллель, лежащая к югу от экватора и короче его на ¹/₂ часового промежутка, которая пройдет через мыс Рапта и Каттигары на расстоянии приблизительно тех же 8⁵/₁₂ градуса от экватора, на которые отстоят от него противолежащие точки земли.

Глава XXIV. Способ правильно изобразить земной шар на плоскости

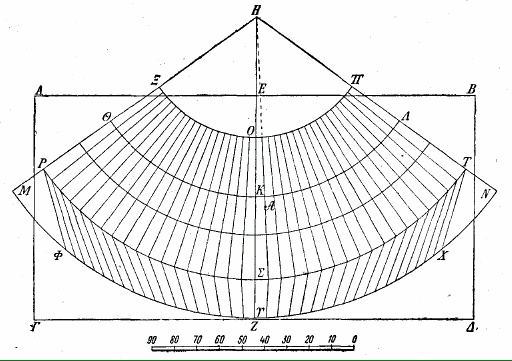
Черт. I.

При черчении карты мы пользуемся следующим способом соразмерного изображения главных параллелей. Приготовиу карту в виде прямоугольного параллелограмаABDG, у кото рого сторона ABприблизительно вдвое длиннее стороны AGПредположим, что AB, как верхняя сторона, будет находиться в северной части чертежа. Затем разделим сторону ABпополам линией EZ, проведенной под прямым углом к ней, и продолжим EZпрямо вверх до точки H, отстоящей на расстоянии таких 34 частей, каких прямая ZHсодержит 131⁵/₁₂. Примем точку Н за центр, а за радиус -- отрезок между Hи точкой, лежащей на HZна расстоянии 79 делений от H, и опишем дугу QKL; она и будет изображать параллель, проходящую через Родос. Чтобы получить крайние пределы длины земли, отстоящие на семь часовых промежутков по обе стороны отK, мы отложим по линии среднего меридиана HZрасстояние, содержащее четыре единицы. Они соответствуют пяти единицам, отложенным по параллели Родоса, так как большой круг земли относится к этой параллели приблизительно как пять к четырем. Отложив по восемнадцати таких расстояний в обе стороны от точки Kпо дугеQKL, мы получим точки, через которые нужно будет провести из центра H меридианы, заключающие третью часть всех часовых промежутков и являющиеся пределами известной нам земли, меридианы HQMи HLN. Будучи так же последовательны, мы проведем параллель Фуле на расстоянии 52 единиц, отлаженных по линии HZот точки H (XOP); экватор -- соответственно на расстоянии 120 делений от точки H (RST); параллель, противолежащую параллели Мероэ и самую южную -- на расстоянии 131⁵/₁₂деления от точки H(MGN). Следовательно отношение дуги RST к дуге XOPравно отношению 115 к 52 и соответствует отношению этих параллелей на сфере, потому что и HS содержит 115 таких единиц, которых HOсодержит 52, и, таким образом, отношение линии HS к линии HOравняется отношению дуги RST к дуге XOP. Отрезок OKмеридиана, то есть расстояние между параллелью, проходящей через Фуле, и параллелью, проходящей через Родос, будет содержать 27 единиц; отрезок KS, то есть расстояние между параллелью Родоса и экватором -- таких же 36 единиц; отрезок SG, то есть расстояние между экватором и параллелью, противолежащей параллели Мероэ, -- таких же 16⁵/₁₂ единицы. Кроме того, если расстояние OG, ширина известной нам земли, содержит 79⁵/₁₂ или целых 80 единиц, то средняя длина земли QKL равняется 144 единицам, что соответствует предположению, сделанному на основании географических описаний. Ведь приблизительно таково же отношение 40000 стадий ширины земли к 72000 стадий длины по параллели Родоса. И остальные параллели мы, если у нас будет такое намерение, проведем опять-таки из центра в точке H и на таких расстояниях от точки S, которые содержат столько делений, сколько соответствует указанным выше расстояниям от экватора. Линии, изображающие меридианы, мы сможем провести в виде непрерывных прямых не до параллели MGN, а всего только до экватора RST. Затем, разбив дугуMGNна деления, величина и число которых равнялись бы величине и числу делений параллели Мероэ, можно будет соединить прямыми наши точки деления с точками деления экватора, чтобы этот поворот линий RFи TC как-то показывал их откло/н/ение к югу по другую сторону экватора. Затем, чтобы было удобнее отмечать наносимые на карту места, мы снова приготовим узкую линеечку, равную по длине линии HZили всего только HS, и прикрепим ее в точке H таким образом, чтобы при перемещении по всей длине карты одно ребро ее точно прикладывалось к прямым меридианов, так как вырез этого ребра совпадает с центром в полюсе. После этого мы разобьем это ребро или на 131 деление, соответствующее HZ, или только на 115 делений, соответствующих HS, и обозначим деления цифрами, начиная отделения, лежащего у экватора. С помощью этих цифровых обозначений можно будет провести и параллели, чтобы, не делая всех делений и обозначений на среднем меридиане чертежа, не смешивать их с обозначениями мест, которые окажутся у этого меридиана. Таким образом, разбив экватор на 180 градусов, соответствующих двенадцати часовым промежуткам, и обозначив их цифрами, начиная от самого западного меридиана, мы будем все время перемещать наше ребро линейки к указываемому градусу долготы. И находя с помощью делений на линейке данную широту, мынадлежащим образом отметим каждый пункт -- точно так же, как это было показано, когда речь шла об изображении на сфере.

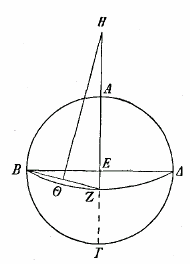
Черт. II.

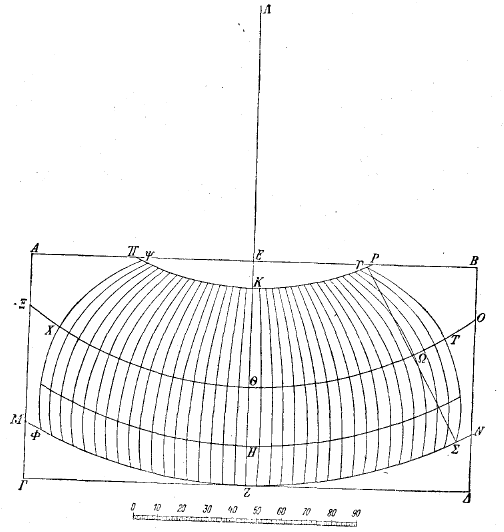
В нашем чертеже вселенной было бы еще больше сходства с очертаниями земли и больше соразмерности с ними, если бы и линии меридианов мы представили в том виде, какой они имеют на глобусе, когда он неподвижен и одна и та же плоскость проходит через глаз, через находящуюся перед глазом точку пересечения меридиана, делящего пополам известную нам землю в длину, и параллели, делящей ее пополам в ширину, и через центр шара, так что противолежащие границы земли одинаково воспринимаются глазом и видны одинаково. Прежде всего, чтобы найти величину угла между кругами параллелей и плоскостью, проходящей через указанную точку пересечения и через центр шара перпендикулярно среднему меридиану известной нам земли, представим себе, что находящееся перед нашими глазами полушарие ограничено большим кругом ABGD, что полуокружностью меридиана, делящего это полушарие надвое, является линия AEGи что находящейся перед глазами точкой пересечения этой полуокружности со средней параллелью известной нам земли является точка E. Затем проведем через точку другую полуокружность большого кругаBED, так, чтобы она была перпендикулярна полуокружности AEG. Ясно, что плоскость ее пройдет через глаз. Отмерив дугу EZв 23⁵/₆градуса (так как именно на столько градусов отстоит экватор от параллели Сиены, а эта параллель проходит приблизительно по середине известной нам земли), проведем через точку Z полуокружность экватора -- BZA. Таким образом, окажется, что угол между плоскостью экватора и прочих параллелей, с одной стороны, и плоскостью, проходящей через глаз, с другой, равняется 23⁵/₆ градуса, содержащимся в дуге EZ. Нужно при этом иметь в виду, что прямые AEZGи BEDзаменяют собой дуги, причем отношениеBEк EZравно отношению 90 к 23⁵/₆. Если продолжить линию GA, то центр, из которого описана дуга BZD, придется на некоторую точку H, и нам нужно найти отношение HZк EB. Проведем для этого прямую ZB. Пусть точка Q делит ее пополам. Проведем прямую QH, которая, естественно, будет перпендикулярна BZ. Но так как EZсодержит 23⁵/₆таких единиц, которых прямая BEсодержит 90, то хорда BZсодержит 93¹/₁₀ этих единиц, угол BZEсодержит 150¹/₃ таких единиц, каких два прямых угла содержат 360, а оставшийся угол QHZсодержит их 29²/₃. Поэтому отношение HZкZQ равно отношению 181⁵/₆ к 46¹¹/₂₀. И если прямая QZ содержит 46¹¹/₂₀ единиц, то прямаяBEсодержит таких единиц 90. Следовательно, если прямая BEсодержит 90 единиц, a ZE -- таких же единиц 23⁵/₆, то прямая HZбудет содержать их 181⁵/₆. Так мы определим точку H, около которой будут описаны все параллели при изображении карты на плоскости.

⇐ Предыдущая 13 14 15 16 171819 20 21 22 Следующая ⇒