Розділ II. Рівняння і нерівності

Завдання 1. 1. Розв'яжітьрівняння з коренями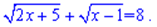
Якщорівняннямає один корінь, упишітьйого у відповідь; якщо два корені - упишітьїх суму.
Розв'язання: Задано ірраціональнерівняння, тому спершудосліджуємо область визначеннякоренів:
2x+5> 0; x> -5/2=-2, 5
x-1> 0; x< 1.
Спільним для двох є інтервал 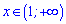, на ньому і будемошукатирозв'язок.
Підносимообидвічастинирівняння до квадрату та спрощуємо

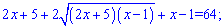
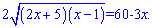
Зновуотрималирівняння з коренем, щобпозбутисяірраціональностіпідносимо до квадрату

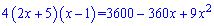
Післягрупуваннядоданківотримаємоквадратнерівняння
x²-372x+3620=0.
Обчислюємодискримінант
D=3722-4*3620=123904
Та коренірівняння

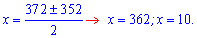
Обидвакорені належать ОДЗ тому за умовоюзавданнязнаходимоїх суму
362+10=372.
Відповідь: 372.

Завдання 2 Розв'яжітьрівняння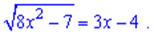
Якщорівняннямає один корінь, упишітьйогопісля слова " Відповідь", якщодекількакоренів, упишітьїх суму.
Розв'язання: Задано рівняння з коренем, тому виписуємо ОДЗ з умовиобмеження на підкореневуфункцію
x²> 7/8.
Даліпідносимо до квадрату обидвічастини і зводимо до квадратного рівняння
8x²-7=9x²-24x+16;
x²-24x+23=0
Оскількикоефіцієнтирізняться на одиницю, то розв'язокзнаходимо за теоремоюВієта.
(x-23)(x-1)=0;
x=23; x=1.
Оскільки x=1 не входить в ОДЗ, то x=23 – єдинийрозв'язокрівняння.
Відповідь: 23.

Завдання3. 36 Розв'яжітьрівняння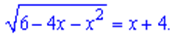
Якщорівняннямаєдекількакоренів, то у відповідьзапишітьїх суму. Якщорівняннямає один корінь, то запишіть у відповідьцейкорінь.
Розв'язання: Для даногорівняння ОДЗ знаходити не будемо, а лишеперевіримокоренівкінціобчисленьпідстановкою. Цедеколидопомагаєзберегтикількахвилин на тестах. Підносимо до квадрату, щобпозбутисяірраціональності
6-4x-x²=x²+8x+16;
2*x²+12*x+10=0;
x²+6*x+5=0.
Обчислюємо дискримінант та коренірівняння
D=62-4*5=36-20=16

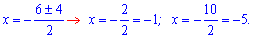
Виконаємопідстановку

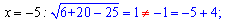
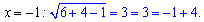
Один коріньзайвий, таким чином x=-1 – коріньірраціональногорівняння.
Відповідь: -1.

⇐ Предыдущая 11 12 13 14 15 16 17 18 1920