Бақылау сұрақтары

⇐ ПредыдущаяСтр 5 из 36Следующая ⇒

Бақ ылау сұ рақ тары

1. Сыртқ ы фотоэффект қ ұ былысы деген не?

2. Фотоэффекттегі «қ ызыл шекара»деген не?

3. Фотоэффект заң дарын тұ жырымдау.

4. Эйнштейн тең деулері негізінде фотоэффектінің екінші жә не ү шінші заң дарын қ орыту.

5. Катод пен анод арасындағ ы фототоктың кернеуге тә уелділік графигіндегі тура жә не кері жү рісті тү сіндіру.

2. ЭЛЕКТРОНДАРДЫҢ ДИФРАКЦИЯСЫ

2. 1. Жұ мыстың мақ саты. Электрондардың поликристалдық жұ қ а пленкадан дифракциялық суретін алу. Электронның толқ ын ұ зындығ ы мен ү деткіш кернеу арасындағ ы де Бройль қ атынасын тексеру. Де Бройль формуласынан алынатын дифракциялық сурет мө лшерінің ү деткіш кернеуден тә уелділігін тексеру. Электронограмма бойынша кристалдық тор жазық тарының ара қ ашық тығ ын анық тау [1, 2, 5-9].

2. 2. Теориялық кіріспе. Жарық тың затқ а фотоэлектрлік жә не фотохимиялық ә сері бойынша эксперименттік деректерді талдау нә тижесінде А. Эйнштейн М. Планктың кванттық гипотезасын кең ейтіп жә не терең дететін жарық тың фотондық теориясын ұ сынды. Фотондық теорияғ а сә йкес электромагниттік ө ріс (жарық ) бө лшектерге ұ қ сас фотондар ағ ыны. Олар затпен 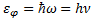белгілі нақ ты энергияғ а жә не 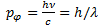импульсқ а иебү тін бө лшек сияқ ты ә серлеседі, мұ ндағ ы 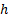–Планк тұ рақ тысы, -жарық жылдамдығ ы; 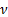- жиілік, 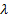- толқ ын ұ зындығ ы. Дегенмен интерференциялық жә не дифракциялық қ ұ былыстарды тү сіндіру ү шін жарық тың толқ ындық табиғ аты жө ніндегі кө ріністің сақ талуы қ ажет. Осылай физикада корпускулалық -толқ ындық дуализм проблемасы пайда болды.

1923 жылы француз физигі Луи де Бройль корпускулалық толқ ындық дуализм барлық материалдық бө лшектерге- электрондарғ а, протондарғ а, атомдарғ а жә не т. т. тә н деген қ орытындығ а келді. Бө лшектердің толқ ындық жә не корпускулалық қ асиеттері арасындағ ы сандық қ атынастар фотондар ү шін қ андай болса, дә л сондай болады: егер бө лшектің энергиясы 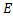жә не импулсі 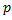болса, онда осы бө лшекпен жиілігі 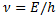жә не толқ ын ұ зындығ ы

(2. 1)

толқ ын байланысқ ан болады.

Потенциалдар айырымы 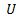электр ө рісімен ү детілген электрондар ү шін де Бройль толқ ын ұ зындығ ын табайық. Осы жағ дайда электрондар

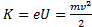(2. 2)

кинетикалық энергия қ абылдайды, релятивтік емес қ арастырғ анда электрондардың импульсі

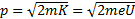(2. 3)

қ атынасымен анық талады. (3)-ті (1)-ге қ ойып

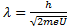(2. 4)

ө рнегін аламыз, мұ ндағ ы, 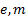-электрондардың заряды мен массасы. Осы формуладан энергиялары 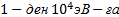дейінгі электрондардың де Бройль толқ ын ұ зындық тары 1-ден 0, 01 нм-ге дейінгі аралық та, яғ ни рентген сә улелерінің толқ ын ұ зындық тарындай болады. Сондық тан электрондардың толқ ындық қ асиеттері, мысалы, бұ лардың кристалдарда шашырау кезінде (яғ ни рентген сә улелерінің дифракциясы бақ ыланатын жағ дайларда) білінуі тиіс. Берілген жағ дайда кристалл табиғ и дифракциялық тор болады.

Энергиялары ондағ ан килоэлектрон вольт (кэВ) болатын электрондардың дифракциясы зерттелгенде бұ лардың жылдамдығ ы жарық жылдамдығ ымен салыстыруғ а келетіндейболады. Осы жағ дайларда электрондардың импулсін анық тау ү шін 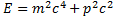жә не 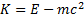релятивтік формулаларды пайдалану керек, мұ ндағ ы 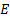-толық энергия. Осы формулалардан 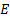-ні шығ арып, (2)-ні ескеріп, мына ө рнекті табамыз:

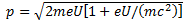(2. 5)

(5)-ті (1)-ге қ ойып, де Бройль толқ ыны ұ зындығ ы ү шінрелятивтік ө рнекті аламыз:

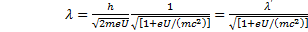(2. 6)

Де Бройль толқ ынында не тербеледі деген сұ рақ тың қ ойылуы заң ды. Де Бройль толқ ынының жалпылай қ абылданғ ан тү сіндірілуі бойынша толқ ындық заң дарғ а бө лшектің кү йін бейнелейтін жә не 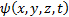толқ ындық функция деп аталатын қ айсыбір шама бағ ынады. Толқ ындық функцияның 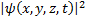квадраты бө лшектің 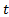уақ ыт мезетінде координаттары 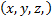нү кте маң ындағ ы бірлік кө лемінде болу ық тималдығ ына тең. 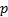импульсі жә не 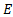энергиясы берілген еркін бө лшектің толқ ындық функциясы де Бройльдің жазық монохроматтық толқ ыны болып табылады

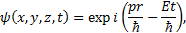
мұ ндағ ы 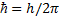. Сонымен, де Бройль толқ ындары – физикалық материалдық қ андайда бір толқ ындар емес ық тималдық амплитудасының толқ ындары. Басқ аша айтқ анда, де Бройль толқ ындарында ық тималдық амплитудасы тербеледі.

Электрондар дифракциясы. Дифракция – толқ ындық қ ұ былыс, ол табиғ аты ә р тү рлі толқ ындар: жарық, дыбыс толқ ындары, сұ йық бетіндегі толқ ындар жә не т. б. таралғ ан кезде бақ ыланады. Бө лшектерде толқ ындық қ асиеттердің болуы бө лшектер ү шін де, соның ішінде электрондар ү шін де дифракцияны мү мкін етеді. Электронның қ айсыбір объектімен – кристалмен, молекуламен жә не т. б. ә рекеттесуі оның қ озғ алысының ө згерісін туғ ызады. Осыдан электронмен байланысқ ан толқ ынның таралу сипаты ө згереді, жә не бұ л барлық толқ ындық қ ұ былыстар ү шін ортақ принциптер бойынша ө теді. Толқ ын объектің барлық нү ктелерімен ә рекеттеседі, ал олар екінші реттік, шашырағ ан толқ ындар кө здеріне айналады. Екінші реттік толқ ындар, біріне бірі қ абаттасып, интерференцияланады. Толқ ындардың кү шейуінің максимум болу шарты: берілген бағ ытта таралатын толқ ындардың 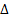жол айырымы 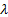толқ ын ұ зындық тардың бү тін санын қ ұ рау керек: 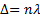, 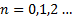. Егерде 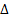жол айырымы 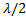жарты толқ ынның тақ санына тең болса (минимум шарты): 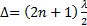, , 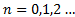онда осы бағ ытта толқ ындар бірін бірі ә лсіретеді. Электрондардың (жә не де рентген сә улелерінің ) кристалдағ ы дифракциясы жағ дайында дифракциялық максимумдардың пайда болу шарты Брэгг-Вульф формуласымен анық талады:

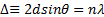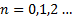, . (2. 7)

мұ ндағ ы 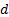–кристаллографиялық жазық тық тардың (кристалдық тор тұ рақ тысы) ара қ ашық тығ ы; 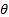-сырғ у бұ рышы, яғ ни тү сетін электрондар шоғ ымен кристаллографиялық жазық тық арасындағ ы бұ рыш (2. 1-сурет).

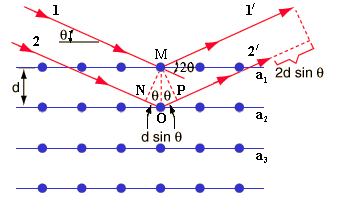
Сурет2. 1 Кристаллографиялық жазық тық тар[27]

Дифракциялық максимумның орнын анық тайтын шағ ылғ ан шоқ тү сетін шоқ бағ ытынан 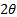бұ рышқ а ауытқ иды.

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒