
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа № 3. Практическая работа № 4
Практическая работа № 3
По табличным данным построить переходную кривую объекта, определить параметры передаточной функции объекта, рассчитать настройки ПИД-регулятора, обеспечивающие 20%-е перерегулирование.
DXвх = 5, 5 кПа; DY = 0, 149 %; tзап = 40 сек
| t, мин | ||||||||||
| DY | 0, 009 | 0, 032 | 0, 060 | 0, 089 | 0, 116 | 0, 130 | 0, 141 | 0, 149 | 0, 149 |
Полученная переходная характеристика изображена на рисунке 5:
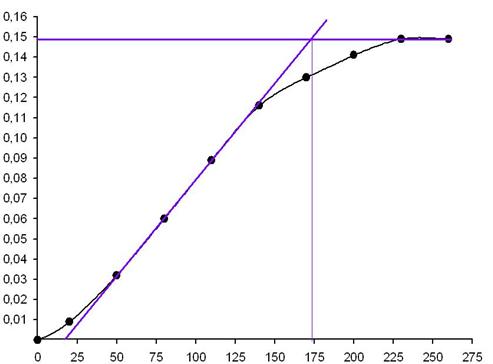
Рис. 5. Переходная характеристика.
Установившееся значение выходной величины составляет:
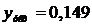 ;
;
Коэффициент усиления равен:
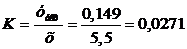 ;
;
Постоянная времени равна:
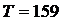 .
.
Для процесса с 20 % перерегулированием ПИД-регулятора, его настройки:
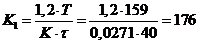 ;
;
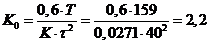 ;
;
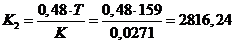 .
.
Практическая работа № 4
Дана одноконтурная АСР. Требуется определить:
· передаточные функции регулятора и объекта управления,
· передаточную функцию разомкнутой системы W∞ (s),
· характеристическое выражение замкнутой системы (ХВЗС),
· передаточные функции замкнутой системы Фз(s) – по заданию,
Фв(s) – по возмущению, ФЕ(s) – по ошибке,
· коэффициенты усиления АСР,
· примерный вид переходных процессов по заданию, ошибке и возмущению,
· устойчивость системы.
Структурная схема АСР:
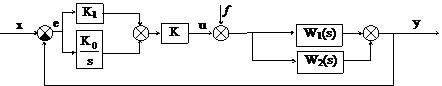 |
W1(s): 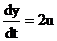 ; W2(s):
; W2(s): 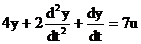 ;
;
K1 = 1, 2; K0 = 1, 0; K = 1, 0
· Передаточная функция регулятора:
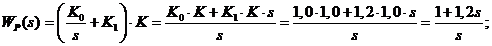 .
.
· Передаточная функция объекта управления:
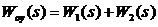 .
.
Определим операторные уравнения звеньев объекта управления: для этого обозначим Y(s) и U(s) как изображения сигналов соответственно y и u, тогда операторные уравнения примут вид:
W1(s): sY(s) = 2U(s);
W2(s): 2s2Y(s)+sY(s)+4Y(s)=7U(s).
Данные уравнения можно преобразовать, вынеся Y(s) и U(s) за скобки:
W1(s): sY(s) = 2U(s);
W2(s): Y(s)·(2s2+s+4)=7U(s).
Отсюда получено:
W1(s): Y(s) = 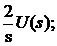
W2(s): Y(s) = 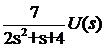 .
.
Тогда:
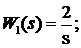
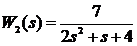 .
.
Передаточная функция объекта управления:
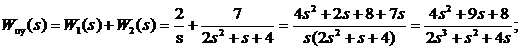
· Передаточная функция разомкнутой системы:
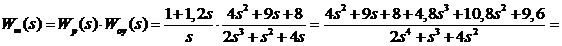
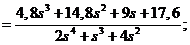
· Характеристическое выражение замкнутой системы:
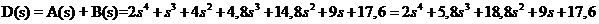
· передаточные функции замкнутой системы
Ф3(s) – по заданию:
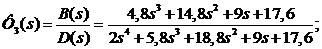
ФЕ(s) – по ошибке:
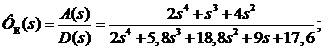
ФВ(s) – по возмущению:
При определении передаточной функции по возмущению принимается Wу. в. = Wоу. Тогда:
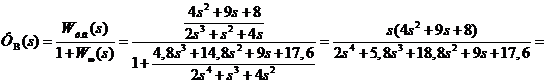
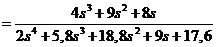 .
.
· По передаточным функциям определим коэффициенты усиления путем подстановки в них s = 0:
К3 = Ф3(0) = 1 – по заданию;
КЕ = ФЕ(0) = 0 – по ошибке;
Кв = Фв(0) = 0 – по возмущению.
· Определим устойчивость АСР по критерию Гурвица.
Так как коэффициенты ХВЗС 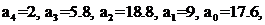 (степень полинома n = 4), то матрица Гурвица имеет вид:
(степень полинома n = 4), то матрица Гурвица имеет вид:
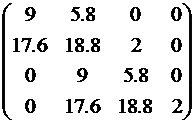
Диагональные миноры матрицы равны соответственно:
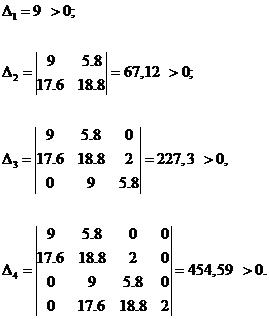
Поскольку все определители положительны, то АСР является устойчивой.
· Определим вид переходных процессов по заданию, ошибке и возмущению:
а) По заданию:
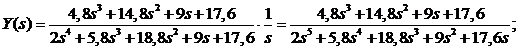
Корни знаменателя:
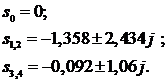
Изображение разбивается на сумму дробей:
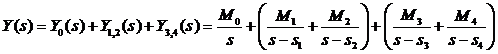 .
.
Тогда оригинал y(t), согласно таблицам, имеет вид:
y(t) = y0 + y1, 2(t) + y 3, 4(t) =
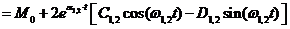 +
+  ;
;
где a1, 2, α 3, 4 и w1, 2, w3, 4 - действительная и мнимая части пары комплексных корней s1, 2 и s3, 4 соответственно.
C1, 2, С3, 4 и D1, 2, D3, 4 – действительная и мнимая части пары коэффициентов М1 и М3 соответственно.
Для корня s0 = 0:
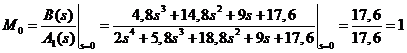 ;
;
Для корней 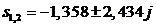 :
:
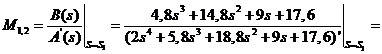 =
= 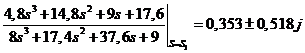 ;
;
Для корней 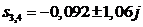 :
:
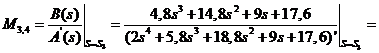
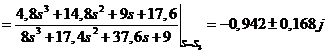 ;
;
Тогда:
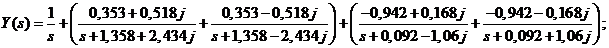
Получим оригинал:
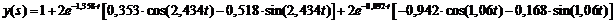
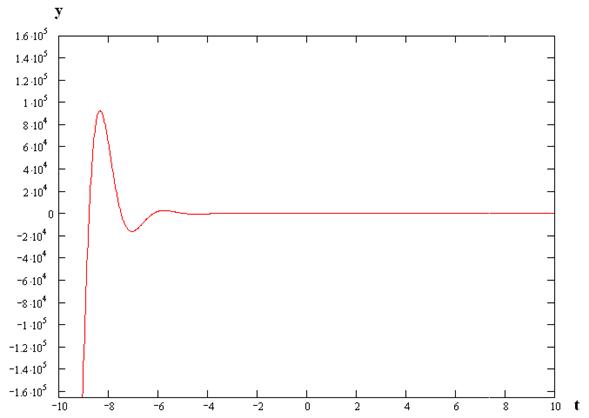
б) По ошибке:
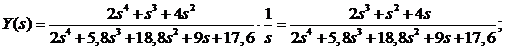
Корни знаменателя:
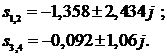
Изображение разбивается на сумму дробей:
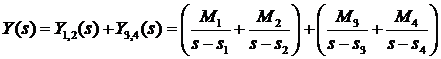 .
.
Тогда оригинал y(t), согласно таблицам, имеет вид:
y(t) = y1, 2(t) + y 3, 4(t) =
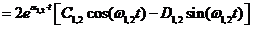 +
+  ;
;
где a1, 2, α 3, 4 и w1, 2, w3, 4 - действительная и мнимая части пары комплексных корней s1, 2 и s3, 4 соответственно.
C1, 2, С3, 4 и D1, 2, D3, 4 – действительная и мнимая части пары коэффициентов М1 и М3 соответственно.
Для корней 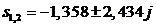 :
:
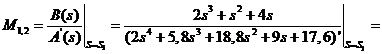
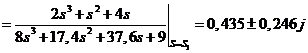
Для корней 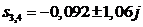 :
:
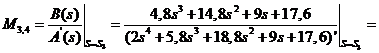
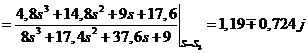 ;
;
Тогда:
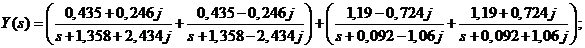
Получим оригинал:
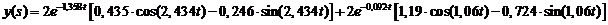
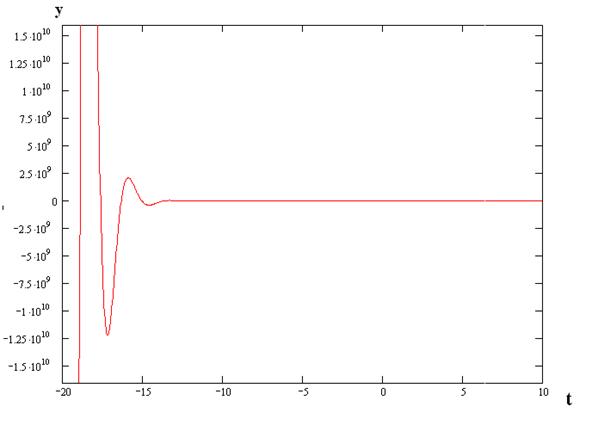
в) По возмущению:
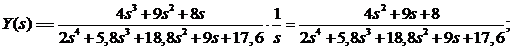
Корни знаменателя:
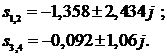
Изображение разбивается на сумму дробей:
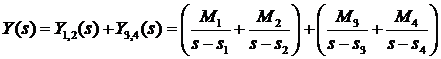 .
.
Тогда оригинал y(t), согласно таблицам, имеет вид:
y(t) = y1, 2(t) + y 3, 4(t) =
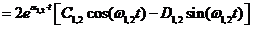 +
+  ;
;
где a1, 2, α 3, 4 и w1, 2, w3, 4 - действительная и мнимая части пары комплексных корней s1, 2 и s3, 4 соответственно.
C1, 2, С3, 4 и D1, 2, D3, 4 – действительная и мнимая части пары коэффициентов М1 и М3 соответственно.
Для корней 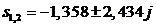 :
:
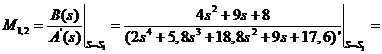
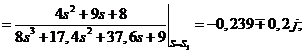
Для корней 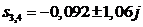 :
:
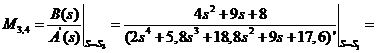
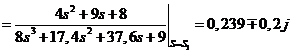 ;
;
Тогда:
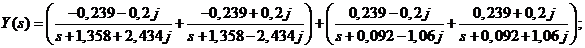
Получим оригинал:
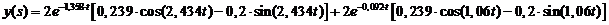
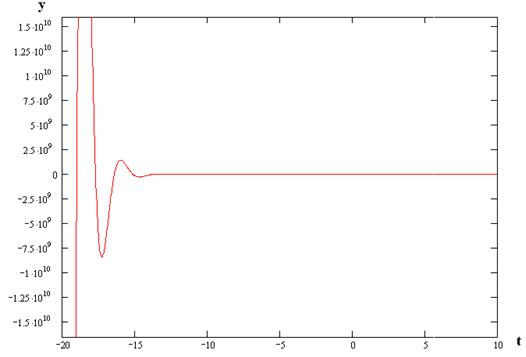
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|