Хелпикс

Главная

Контакты

Случайная статья



Практическая работа № 2

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒


 

 

 

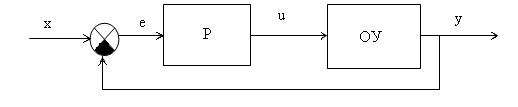
Дана одноконтурная АСР, для которой определена передаточная функция регулятора (Р) с настройками и дифференциальное уравнение объекта управления (ОУ). Требуется определить:

- передаточную функцию разомкнутой системы W∞ (s),

- характеристическое выражение замкнутой системы (ХВЗС),

- передаточные функции замкнутой системы Фз(s) – по заданию, Фв(s) – по возмущению, ФЕ(s) – по ошибке,

- коэффициенты усиления АСР,

- устойчивость системы.

Р - ПИ-регулятор с ПФ вида ;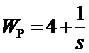

дифференциальное уравнение объекта управления:

 

.


Определим передаточную функцию объекта:

Wоб(s) .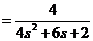

 

Передаточная функция разомкнутой системы имеет вид:

 

 

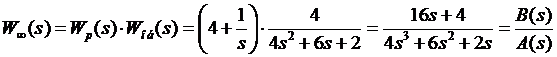
Характеристическое выражение замкнутой системы:

 

;

 

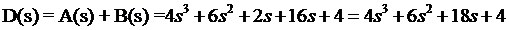Передаточные функции замкнутой системы:

 

 - по заданию;

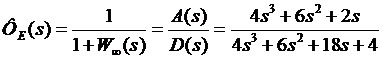 - по ошибке;

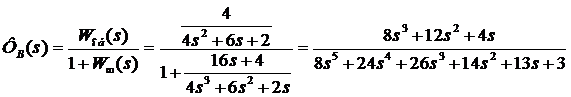 - по возмущению.

 

По передаточным функциям определим коэффициенты усиления путем подстановки в них s = 0:

К3 = Ф3(0) = 1 – по заданию;

КЕ = ФЕ(0) = 0 – по ошибке;

Кв = Фв(0) = 0 – по возмущению.

Определим устойчивость АСР по критерию Гурвица.

Так как коэффициенты ХВЗС а3 = 4, а2 = 6, а1 = 18, а0 = 4 (степень полинома n = 3), то матрица Гурвица имеет вид:

 

 

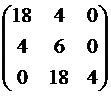
Диагональные миноры матрицы равны соответственно:

 

 

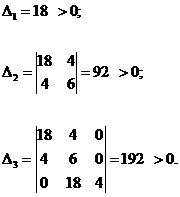
Поскольку все определители положительны, то АСР является устойчивой.


⇐ Предыдущая123Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.