
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа № 1
1. По заданным дифференциальным уравнениям определить операторные уравнения при нулевых начальных условиях, передаточные функции, структурные схемы звеньев, характеристические уравнения и их корни. Показать распределение корней на комплексной плоскости.
Оценить устойчивость каждого из звеньев.
а) 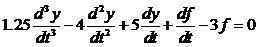 ; б)
; б) 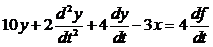 .
.
2. По заданной передаточной функции записать дифференциальное уравнение:
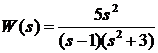 .
.
1. а). Дифференциальное уравнение можно записать в виде:
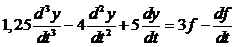 .
.
Обозначим Y(s) и F(s) как изображения сигналов соответственно y и f, тогда операторное уравнение (при нулевых начальных условиях) примет вид:
1, 25s3Y(s) – 4s2Y(s) + 5sY(s) = 3F(s) – sF(s).
Данное уравнение можно преобразовать, вынеся Y(s) и F(s) за скобки:
Y(s). (1, 25s3 – 4s2 + 5s) = F(s). (3 – s).
Отсюда получено:
 .
.
Очевидно, что входной сигнал x отсутствует, и выходной сигнал у определяется только внешним воздействием f (система, действующая по возмущению): 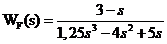 , то получается уравнение Y(s) = WF(s). F(s). Структурная схема объекта приведена на рис. 1.
, то получается уравнение Y(s) = WF(s). F(s). Структурная схема объекта приведена на рис. 1.
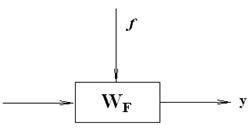
Рис. 1
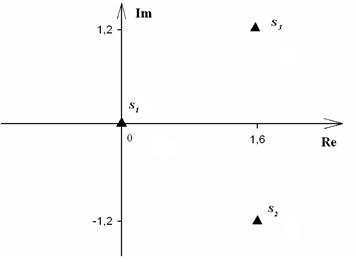
Рис. 2
Передаточная функция имеет знаменатель, называемый характеристическим выражением:
A(s) = 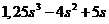 .
.
Если приравнять данное выражение к нулю, то образуется характеристическое уравнение 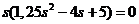 , корни которого:
, корни которого:
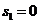 ,
, 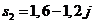 и
и 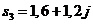 .
.
Распределение корней на комплексной плоскости показано на рис. 2. По рисунку видно, что корни лежат в правой полуплоскости, следовательно, объект неустойчив.
б) Дифференциальное уравнение можно записать в виде:
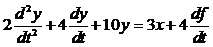 .
.
Обозначим Y(s), X(s) и F(s) как изображения сигналов соответственно y, x и f, тогда операторное уравнение (при нулевых начальных условиях) примет вид:
2s2Y(s) + 4sY(s) + 10Y(s) = 3X(s) + 4sF(s).
Данное уравнение можно преобразовать, вынеся Y(s) и X(s) за скобки:
Y(s). (5s2 + 4s + 10) = 3X(s) + 4sF(s).
Отсюда получено:
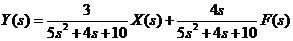 .
.
Если обозначить передаточные функции объекта как
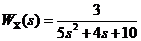 и
и 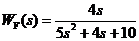 ,
,
то получается уравнение Y(s) = Wx(s). X(s) + WF(s). F(s). Структурная схема объекта приведена на рис. 3.
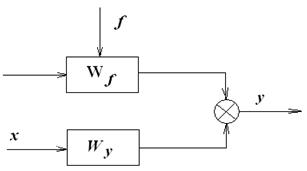
Рис. 3
Характеристическая функция имеет вид:
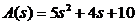 ,
,
а характеристическое уравнение:
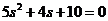 .
.
Корни этого уравнения равны:
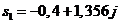 и
и 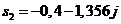 .
.
Распределение корней на комплексной плоскости показано на рис. 4:
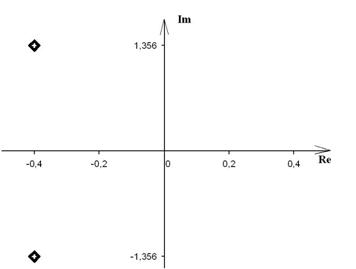
Рис. 4.
Все корни характеристического уравнения лежат в левой полуплоскости, очевидно, что объект устойчив.
2. Дана передаточная функция вида:
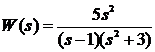
Зная, что по определению, 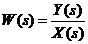 , получим:
, получим:
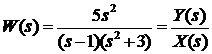 , тогда:
, тогда:
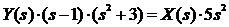 .
.
Раскрывая скобки:
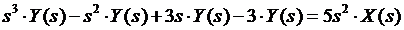
Применяя к полученному выражению обратное преобразование Лапласа, находим искомое дифференциальное уравнение:
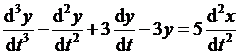 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|