
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
является общезначимой (тавтологией). Поэтому
Пусть À ′ = (А'; ) – какая – то другая алгебраическая система, однотипная с алгебраической системой À, Ì ′ *=(А′; ) - модель, представляющая (задающая) систему À ′. Допустим, что задан гомоморфизм h: À → À ′. Возникает вопрос: будет ли отображение h гомоморфизом модели Ì * в модель Ì ′ *? Положительный ответ на этот вопрос дает следующее утверждение.
70. Отображение h алгебраической системы À = (А; W; W0) в (на) однотипную алгебраическую систему À ¢ = (А¢ ; W¢; W0¢ ) тогда и только тогда является гомоморфизмом, когда h – гомоморфизм модели Ì *, представляющей алгебраическую систему À, в (на) модель Ì ¢ *, представляющей алгебраическую систему À ¢.
Доказательство. Необходимость . Пусть h: Ì *→ Ì '*- гомоморфизм модели Ì * в (на) модель Ì ′ *, 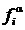 ,
, 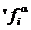 - одноименные главные a - арные (a = 0, 1, …, n) операции алгебраической системы À и À ';
- одноименные главные a - арные (a = 0, 1, …, n) операции алгебраической системы À и À '; 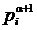 ,
, 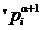 - соответствующие (a+ 1) – арные отношения (предикаты) моделей Ì *, Ì '*;
- соответствующие (a+ 1) – арные отношения (предикаты) моделей Ì *, Ì '*;  произвольные элементы из основного множества А.
произвольные элементы из основного множества А.
Так как h: Ì * → Ì '* является гомоморфизмом, то выполнены условия
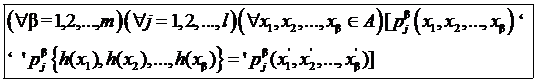 и
и
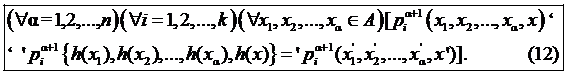 Обозначим
Обозначим 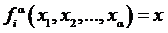 . Тогда предикатная формула
. Тогда предикатная формула
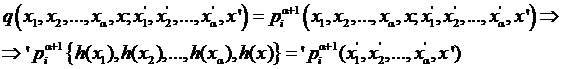
является общезначимой (тавтологией). Поэтому
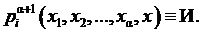
Отсюда и из условия (12) с учетом вида формулы q, имеем
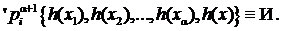 (13)
(13)
В противном случае, согласно операции импликации Þ имели бы, что формула
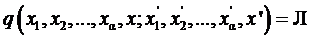 .
.
С учетом введенного обозначения, равенство (13) означает, что
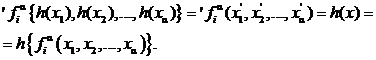 (14)
(14)
Переставив левые и правые части равенства (14), видим, что выполнено условие (2) гомоморфизма алгебраической системы À в (на) алгебраическую систему À '.
Достаточность. Обратное утверждение проверяется так же.
Что требовалось доказать.
Пример 2. Показать, что ортогональное проектирование векторов пространства R3 на координатную плоскость XOY является эпиморфизмом алгебраической системы Å 3 = (Е3; +, fl; ||) на Å 2 = (Е2; Å, fl; ||), где Å, fl - сложение векторов и умножение векторов на числа (скаляры) на плоскости XOY.
Решение. Выделим в R3 координатную плоскость 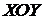 и обозначим через Е2 множество векторов этой плоскости (рис. 29. 4).
и обозначим через Е2 множество векторов этой плоскости (рис. 29. 4).
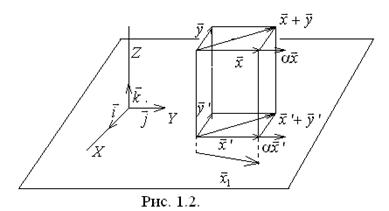 |
Ортогональное проектирование векторов пространства E3 на
эту плоскость является гомоморфизмом.
Выполнение условий (1) определения 5 вытекает из известных свойств проекций (см. также рис. 29. 4):
1) 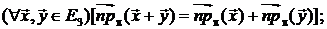
2) 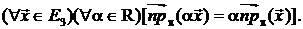
Выполнение условия (6¢ ) гомоморфизма очевидно, так как 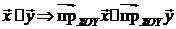 .
.
Это отображение не является инъективным, так как два различных вектора (например, на рис. 29. 4 это векторы 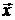 и
и 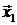 ) могут иметь одну и ту же проекцию. Поскольку множество векторов пространства R3 полностью отображается на множество векторов плоскости
) могут иметь одну и ту же проекцию. Поскольку множество векторов пространства R3 полностью отображается на множество векторов плоскости 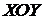 , то отображение проектирования сюръективное.
, то отображение проектирования сюръективное.
Следовательно, 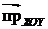 – эпиморфизм алгебраической системы Å 3 = (Е3; +, fl; ||) на Å 2 = (Е2; Å, fl; ||).
– эпиморфизм алгебраической системы Å 3 = (Е3; +, fl; ||) на Å 2 = (Е2; Å, fl; ||).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|