142.Основные свойства гомоморфизмов и изоморфизмов алгебраических систем.

Замечание 1. Отметим случай, когда (при некотором s = 1, 2, 3, …., k) – нульместная операция, т. е. она выделяет (фиксирует) какой-то элемент алгебраической системы À. Тогда, соответствующая ей из À ¢ операция, тоже будет нульместной и, значит, выделит какой-то элемент алгебраической системы À ¢. В этом случае условие (1) примет вид

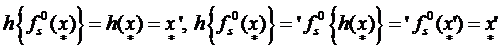(3)

или

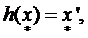(4)

т. е. выделенный элемент 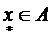переходит при отображении h в соответствующий ему выделенный элемент 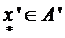(рис. 1).

Замечание 2. Условие сохранения отображением h главной бинарной операции * алгебраической системы А, которой соответствует главная бинарная операция Ä алгебраической системыÀ ¢ , в случаях когда эти операции могут быть сложением и умножением, приводится в следующей таблице

Таблица 29. 1

№ п. п.	Бинарная операция на А	Бинарная операция на А¢	Условие сохранения бинарной операции алгебраической системы À
	*	Ä	(" x, yÎ A)[h(x * y) = h(x) Ä h(y) = = x¢ Ä y¢ ]
	+	Å	(" x, yÎ A)[h(x + y) = h(x) Å h(y) = = x¢ Å y¢ ]
	+	⊙	(" x, yÎ A)[h(x + y) = h(x) ⊙ h(y) = =x¢ ⊙ y¢ ]
	×	Å	(" x, yÎ A)[h(x × y) = h(x) Å h(y) = = x¢ Å y¢ ]
	×	⊙	(" x, yÎ A)[h(x * y) = h(x) ⊙ h(y) = = x¢ ⊙ y¢ ]

Следовательно, для бинарных операций «сложения» и «умножения» условие (1) означает, что при отображении h сумма «+» и произведение «× » любых двух элементов х и у из А переходят в сумму в контуре Å или произведение в контуре Ä соответствующих элементов h(x) = x¢ и h(y) = y¢ из А.

ОПРЕДЕЛЕНИЕ 3. Говорят, что отображение h: А ® А¢ сохраняет главное отношение 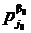алгебраической системы À, если

выполняется условие

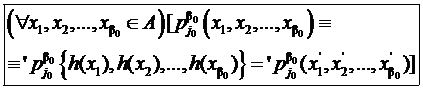. (5)

ОПРЕДЕЛЕНИЕ 4. Говорят, что отображение h: А ® А¢ сохраняет главные отношения алгебраической системы À, если условие (5) выполняется для всех главных отношений 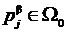алгебраической системы À, т. е. если

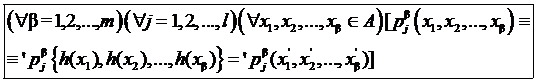(6)

ОПРЕДЕЛЕНИЕ 5. Гомоморфизмом алгебраической системы À = (А; W; W₀) в однотипную ей алгебраическую систему À ¢ = (А; W¢; W₀¢ ) называется отображение h: A ® A¢, сохраняющее все главные операции алгебраической системы À и удовлетворяющее условию

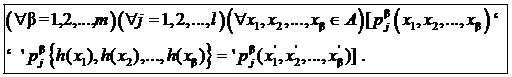(6¢ )

Алгебраические системы À и À ¢ называются гомоморфными, если существует гомоморфизм алгебраической системы À в À ¢. Запись À ¥ À ¢ означает, что алгебраические системы À и À ¢ гомоморфные.

Слово «гомоморфизм» – греческое. «Homos» означает «подобие», «одинаковый», «равный», а «morph» – «форма», «вид», «образ», «структура», «строение». Термин «гомоморфный» означает в переводе с латинского языка «подобный по форме (строению, структуре)».

Обозначим множество всех гомоморфизмов алгебраической системы À в алгебраическую систему À ' через Hom (À, À ¢ ) или через Hom (А, А ¢ ).

ОПРЕДЕЛЕНИЕ 6. Гомоморфизм h: A ® A¢ алгебраической системы À в алгебраическую систему À ' называется моно -морфизмом (или вложением) алгебраической системы À в алгебраическую систему À ¢, если отображение h является инъективным.

Приставка «моно» – греческого происхождения, означает «один», «единственный».

ОПРЕДЕЛЕНИЕ 7. Гомоморфизм h: À ®À ¢ алгебраической системы À в алгебраическую систему À ¢ называется эпиморфизмом, если отображение h является сюръективным.

Приставка «эпи» – греческого происхождения, означающая «при», «после», «возле». Эпиморфизм – это «сокращенный слева» гомоморфизм f(x₁) = f(x₂) Þ (x₁ = x₂).

Гомоморфизм h алгебраической системы À в себя называется эндоморфизмом.

Слово «эндоморфизм» – греческое; «endon» – означает «внутри».

Обозначим множество всех эндоморфизмов алгебраической системы À через End (À ) или через End (А).

ОПРЕДЕЛЕНИЕ 8. Изоморфизмом алгебраической системы À на однотипную алгебраическую систему À ¢ называется биективное отображение h: À ® À ¢ , сохраняющее все главные операции и «главные отношения» алгебраической системы À.

Алгебраические системы À и À ¢ называются изоморфными, если существует изоморфизм алгебраической системы À на алгебраическую систему À ¢. Запись À @ À ¢ означает, что алгебраические системы À и À ¢ изоморфны.

Приставка «изо» (isos) – греческого происхождения, означающая «равный», «одинаковый», «подобный».

Термин «изоморфный» означает в переводе с латинского «одинаковый по форме (строению, структуре)».

Каждый изоморфизм алгебраической системы À на алгебраическую систему À ¢ есть гомоморфизм. Но утверждение, что каждый биективный гомоморфизм есть изоморфизм в общем случае неверно. Однако, всякий гомоморфизм h конечной алгебраической системы А на себя является изморфизмом.

Изоморфизм алгебраической системы À на себя называется автоморфизмом. Приставка «авто (autos)» – греческого происхождения, означающая «сам».

Множество всех автоморфизмов алгебраической системы À обозначается через Аut(À ) или через Аut (А).

Для алгебры À (W₀= Æ ) и для модели Ì (W = Æ ) все вышеприведенные понятия, определения и утверждения остаются в силе. При этом выражение «алгебраическая система» необходимо заменить на слово «алгебра» или на слово «модель».

Пример 1. Пусть А = Z, A¢ = {-1; 0; 1}. Показать, что алгебра Z = (Z; × ) гомоморфна алгебре A ¢ = (А¢; × ).

Решение. Данные алгебры Z и À ¢ однотипные на множествах Z и А¢.

Определим отображение h алгебры Z в алгебру À ¢ следующим образом

1, если a > 0,

(" aÎ Z)[h(a) = 0, если a = 0, (7)

-1, если a < 0.

Покажем, что отображение (7) будет гомоморфизмом. Пусть n и m –любые натуральные числа. В этом случае имеем:

h(n) = 1, h (m) = 1, h (-n) = -1, h (-m) = -1.

Так как

n × m Î Z₊, n × (-m )Î Z _-, (- n) × m Î Z _-, (-n)× (-m ) Î Z₊,

n × 0 = (-n ) × 0 = 0 × m = 0 × (m) = 0,

то имеем

h(n × m) = 1 = 1 × 1 = h(n) × h(m),

h(n × (-m)) = -1 = 1 × (-1) = h(n) × h(-m),

h((-n) × m) = -1 = (-1) × 1 = h(-n) × h(m),

h((-n) × (-m)) = 1 = (-1) × (-1) = h(-n) × h(-m),

h(n × 0 ) = 0 = 1 × 0 = h(n) × h(0),

h(0 × m) = 0 = 0 × 1 = h(0) × h(m),

h((-n) × 0) = 0 = (-1) × 0 = h(-n) × h(0),

h(0 × (-m)) = 0 = 0 × (-1) = h(0) × h(-m).

Написанные равенства означают, что

(" а, b Î Z)[ h(а × b) = h(а) × h(b)],

то есть что отображение h является гомоморфизмом.

Значит, алгебра Z= (Z; × ) ~ À ¢ = (A¢; × ).

Что требовалось доказать.

142. Основные свойства гомоморфизмов и изоморфизмов алгебраических систем.

1⁰, (2⁰). Пусть h₁ – гомоморфизм (изоморфизм) алгебраической системы À =(А; W; W₀) в (на) алгебраическую систему À ¢ =(A¢, W¢; W₀¢ ) и h₂– гомоморфизм (изоморфизм) алгебраической системы À ¢ в (на) алгебраическую систему À ¢ ¢ = (A¢ ¢, W¢ ¢; W₀¢ ¢ ). Тогда их композиция (произведение) h₂°h₁ (h₁× h₂) является гомоморфизмом (изоморфизмом) алгебраической системы À в (на) алгебраическую систему À ¢ ¢ .

Доказательства. Доказательство свойства 1°. 1). Пусть 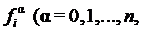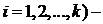произвольные главные операции алгебраической системы À , а 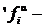соответствующие им главные операции алгебраической системы À ¢ и 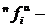главные операции алгебраической системы À ², соответствующие операциям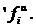

Надо доказать, что для любых элементов 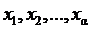из основного множества 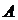алгебраической системы À выполняется условие

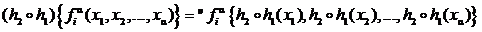. (8)

По определению композиции отображений, имеем

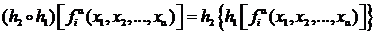. (9)

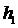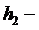Так как, по условию, и гомоморфизмы, то из (9) получаем

то есть выполняется равенство (8).

2). Поскольку 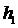и 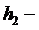гомоморфизмы, то применяя (6¢ ) и закон транзитивности равносильности предикатов, получаем

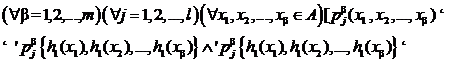
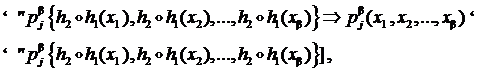
то есть отображение 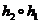сохраняет и главные отношения алгебраической системы À .

Итак, h₂°h₁ является гомоморфизмом алгебраической системы À в алгебраическую систему À ¢ ¢ . Тогда, как говорят, имеется диаграмма

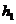
À À ¢ ,

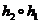
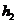
À ¢ ¢

Рис. 29. 2

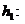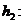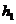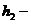Доказательство свойства 2°. 1). Пусть теперь À ® À ¢ и À ¢ ® À ¢ ¢ являются изоморфизмами. Тогда так как и биективные отображения, то согласно свойствам отображений следует, что их композиция 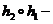тоже биективное отображение.

2). Поскольку 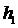и 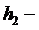изоморфизмы, то применяя (6) и закон транзитивности равносильности предикатов, получаем

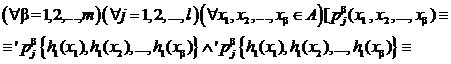
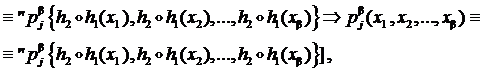
то есть отображение 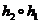сохраняет и главные отношения алгебраической системы À .

Следовательно, 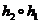: À ® À ¢ ¢ является изоморфизмом алгебраической системы À на алгебраическую систему À ¢ ¢ ..

Этот результат также можно изобразить диаграммой

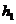
À À ¢ ,

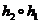
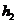
À ¢ ¢

Рис. 29. 3

Что требовалось доказать.

3⁰. Пусть h – изоморфизм алгебраической системы À =(А; W; W₀) на алгебраическую систему À ¢ = (А¢ ; W¢; W¢ ₀). Тогда отображение h^-¹является изоморфизмом алгебраической системы À ¢ на алгебраическую систему À .

Доказательство. Согласно определению изоморфизма алгебраических систем, h - биективное отображение алгебраической системы À на алгебраическую систему À ¢ , удовлетворяющее условиям (2) и (6). Поэтому, во-первых, по свойствам отображений 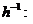À ¢ ® À является биективным, во-вторых, мы покажем, что 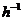сохраняет главные операции 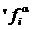и отношения 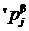алгебраической системы À ¢, т. е. выполняются условия:

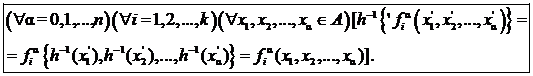(10)

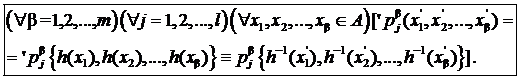(11)

Условие (10) равносильно следующему условию («свернули» обе части условия (10) с отображением 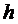и переставили левые и правые части полученного условия и применили равенство )

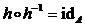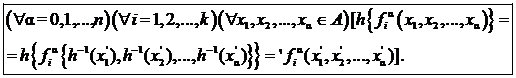(10¢ )

Так как по условию свойства 3°, h – изоморфизм алгебраической системы À на алгебраическую систему À ¢ , то выполнено условие (7), которое равносильно (10¢ ). Следовательно, выполняются условия (10¢ ) и (1).

Условие (11), очевидно, равносильно следующему

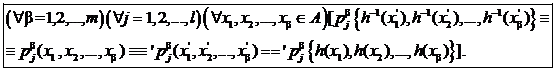которое выполнено в силу того, что 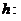À ® À ¢ - изоморфизм.

Итак, 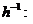À ¢ ® À -- изоморфизм.

Что требовалось доказать.

4⁰. Отношение изоморфизма между однотипными алгебраическими системами является отношением эквивалентности.

Доказательство. На множество всех однотипных алгебраических систем отношение изоморфизма между алгебраическими системами является:

а) рефлексивным, т. к. очевидно, что каждая алгебраическая система À изоморфна самой себе: À @ À ¢, h = id_À;

б) симметричным: À @ À ¢ Þ À ¢ @ À, по свойству 3⁰;

в) транзитивным: À @ À ¢ Ù À ¢ @ À ¢ ¢ Þ À @ À ¢ ¢ по свойству 2⁰.

Что требовалось доказать.

Из свойства 4⁰ следует, что все алгебраические системы данного типа распадаются на классы изоморфных между собой систем. Алгебраические системы преимущественно изучаются с точностью до изоморфизма. Таким образом, все алгебраические системы данного класса изоморфных алгебраических систем с точки зрения определенных на них алгебраических операций и отношений ничем не отличаются одна от другой; они могут отличаться лишь природой своих элементов и, возможно, названием заданных на них операций и отношений и символикой, с помощью которых они записываются. Поэтому изоморфные алгебраические системы считаю лишь различными экземплярами одной и той же алгебраической системы.

Заметим, что понятие изоморфизм не являются специфичным для алгебры. Всякая математическая наука умеет по некоторым признакам иденфицировать изучаемые ею объекты (вводить понятие эквивалентности объектов и разбивать множество их на классы эквивалентности), выделяя тем самым те свойства объектов, которые составляют предмет этой науки.

Теория алгебраических систем изучает лишь те свойства алгебраических систем, которые cохраняются при изоморфизме, таким образом, одинаковы у всех алгебраических систем. Эти свойства часто называют абстрактными свойствами системы. Считается, что абстрактные свойства системы – это свойства главных операций и отношений системы, не зависящее от природы элементов, слагающих системы.

Примерами наиболее простых абстрактных свойств систем могут служить тип

τ (À ) ,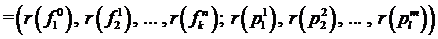

и мощность 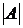системы, т. к. они у изоморфных систем заведомо одинаковы.

5⁰, (6⁰). При гомоморфизмах (изоморфизмах) одной алгебраической системы в другую образами подсистем и непустыми полными прообразами подсистем являются подсистемы:

5) (" h: À ® À ¢ )[À ₁≺ À Þ h(À ₁) ≺ À ¢ ];

6) (" h: À ® À ¢ )[($h^-1: À ¢ ®À )Ù À ₁¢ ≺ À ¢ Þ h^-1(À ₁¢ )≺ À ].

Доказательства. Докажем, например, свойство 5⁰.

1) Пусть h - гомоморфизм алгебраической системы À = 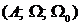в алгебраическую систему À ¢ = (А¢; W¢; W¢ ₀) и пусть À ₁= (А₁; W₁; W₀₁) -- подсистема алгебраической системы À : À ₁ ≺ À.

Возьмем произвольную главную операцию 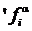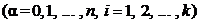алгебраической системы À ¢ и произволь -ные элементы 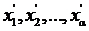в образе h(А₁) подмножества А₁ алгебраической системы À . Обозначим через 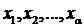какие - нибудь прообразы элементов 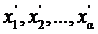в А₁, и пусть .

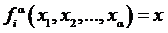Из формулы (2) получаем

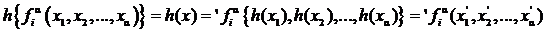Так как 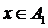, то 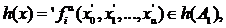, т. е. подмножество h(А₁) замкнуто относительно главной операции 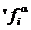алгебраической системы À ¢ , и первое утверждение свойства 5⁰ доказано.

2) Обратное утверждение доказывается аналогичными рассуждениями (доказательство предлагается читателю в качестве упражнения).

Доказательство можно найти на стр. 57, теорема 3 в монографии Мальцева А. И. Алгебраические системы. –М.: Наука, 1970. -392 с.

Что требовалось доказать.

СЛЕДСТВИЕ 5. 1 (6. 1). При любом гомоморфизме (изоморфизме) h: À ® À ¢ образ алгебраической системы À является подсистемой алгебраической системы À ¢: h (À ) ≺ À ¢.

С каждой алгебраической системой À = 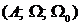мы связы -вали (§28) однозначно определенную модель M* = (А; 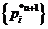, {p_j^β}) (или кратко M* = (А; W₀*) ), которая называется моделью, представляющей алгебраическую систему À.

⇐ Предыдущая 123 Следующая ⇒