Импульс переменной силы

Если сила непостоянна по величине или по направлению, то для определения ее импульса за данный промежуток времени надо разбить этот промежуток времени на столь малые интервалы, в течение которых можно пренебречь изменением силы, и определить для каждого такого интервала элементарный импульс. Элементарным импульсом силы называют импульс за столь малый промежуток времени, при котором можно пренебречь изменением силы:
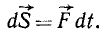(164)

Импульс переменной силы за конечный промежуток времени выражают пределом геометрической суммы элементарных импульсов за бесконечно малые части данного промежутка:

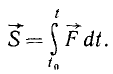(164^/)

Следовательно, импульс переменной силы за данное время выражается интегралом от вектора 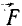по скалярному аргументу t.

Для вычисления импульса переменной силы пользуются его проекциями на оси координат. Построим прямоугольную систему координат и спроецируем элементарный импульс на ось Ох:

dS_x = Fdtcosa_F= X dt.

Интегрируя в пределах от t₀ до t, находим S_x и аналогично S_y и S_z:

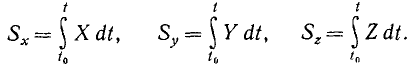(165)

По проекциям (165) легко определить модуль и направляющие косинусы вектора, однако в этом редко встречается необходимость и практически обычно ограничиваются определением проекций (165).

Проекция импульса равнодействующей на любую ось равна сумме проекций импульсов составляющих сил на ту же ось:

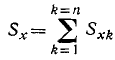
Пусть на точку действует несколько сил, проекции которых на какую-либо ось Ox обозначим X1, X2, ..., Х„, а проекцию ' равнодействующей этих сил обозначим X. Тогда

X = X₁ + X₂ +... + Х_n.

Умножим обе части этого равенства на бесконечно малый промежуток времени dt и проинтегрируем в пределах от t₀ до t:

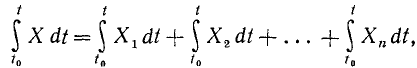
или

S_x = S_xl + S_x2 +... + S_xn. (166)

Итак, проекция импульса равнодействующей на любую ось за данный промежуток времени равна алгебраической сумме проекций импульсов составляющих сил на ту же ось и за то же время, следовательно, импульс равнодействующей равен геометрической сумме импульсов составляющих:
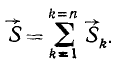(166^/)

Домашнее задание:

1. Выполните конспект

2. Запишите задачи

⇐ Предыдущая 123 4 5 6 7 Следующая ⇒