Сопряжение двух пересекающихся прямых

При изучении дисциплины «Инженерная графика» студенты должны усвоить правила и последовательность выполнения геометрических построений и сопряжений. В этом отношении лучшим способом приобретения навыков построения являются задания по вычерчиванию контуров сложных деталей.

Прежде чем приступить к выполнению контрольного задания, нужно изучить технику выполнения геометрических построений и сопряжений по методическому пособию.

Сопряжения линий

Сопряжением называется плавный переход от одной линии к другой. Для построения любого сопряжения дугой заданного радиуса нужно найти:

Центр сопряжения – центр, из которого проводят дугу;
Точки сопряжения (касания) – точки, в которых одна линия переходит в другую.

Центр сопряжения находится от точек сопряжения на одинаковых расстояниях, равных радиусу сопряжения R. Переход от прямой к окружности будет плавным в том случае, если прямая касается к окружности. Точка сопряжения К лежит на перпендикуляре, опущенном из центра О окружности к прямой (рис. 1)

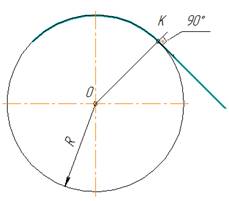
рис. 1

Переход от одной окружности к другой будет плавным, если окружности касаются.

Различают два случая касания дуг окружностей: внешнее (рис. 2) и внутреннее (рис. 3).

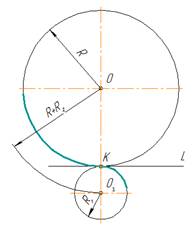
При внешнем касании центры окружностей лежат по разные стороны от их общей касательной L (рис. 2). Расстояние между их центрами ОО₁ равно сумме радиусов окружностей R+R₁ и точка касания лежит на прямой ОО₁, соединяющей их центры.

При внутреннем касании центры окружностей лежат по одну сторону от их общей касательной L. Расстояние между их центрами ОО₁ равно разности их радиусов R-R₁ и точка касания К окружностей лежит на продолжении прямой ОО₁ (рис. 3).


рис. 2	рис. 3

Касание дуг окружностей:

рис. 2 – сопряжение двух окружностей (внешнее касание)

рис. 3 – сопряжение двух окружностей (внутреннее касание)

Сопряжение двух пересекающихся прямых

Даны пересекающиеся под прямым, острым и тупым углами прямые линии.

Требуется построить сопряжения этих прямых дугой заданного радиуса R.

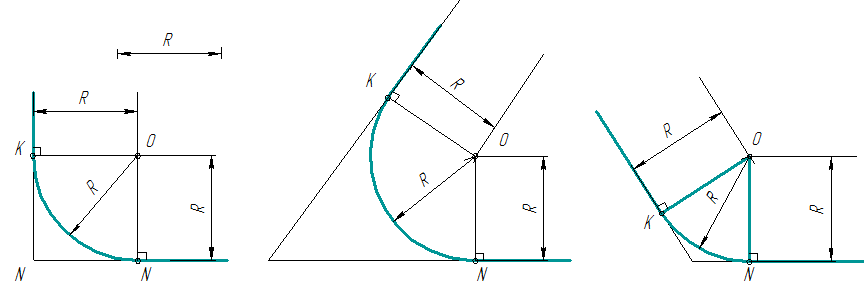
рис. 4

Для нахождения центра сопряжения проводят вспомогательные прямые, параллельные данным на расстоянии равном радиусу R. Точка пересечения этих прямых т. О и будет центом дуги сопряжения (рис. 4).
Перпендикуляры, опущенные из центра дуги сопряжения т. О на данные прямые, определяют точки касания К и N.
Из точки О, как центра, описывают дугу заданного радиуса R.

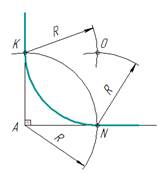
рис. 5

Примечание. Для прямых углов центр сопряжения удобнее находить с помощью циркуля (рис. 5).

12 3 Следующая ⇒