Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

2.3 Теңсіздіктерді дәлелдеуге векторлар құру тәсілі

2. 3 Тең сіздіктерді дә лелдеуге векторлар қ ұ ру тә сілі

Мысал 10: Тең сіздікті дә лелдең із: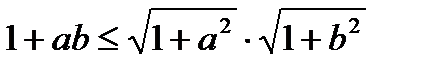

Дә лелдеу:   Вектор қ ұ рамыз 

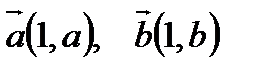
Скаляр кө бейтінді орындасақ  

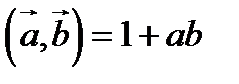
Ұ зындық тарын табатын болсақ   

Мына тең сіздік ақ иқ ат 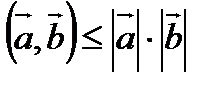 , олай болса  

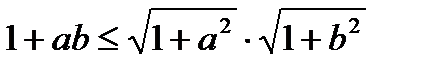
Дә лелдеу керегі де осы еді.

Мысал 11:  екенін ескеріп, мына тең сіздікті дә лелдең із [6]:

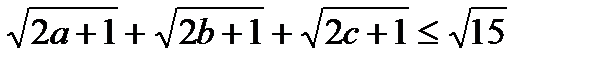
Дә лелдеу:   Екі вектор қ ұ рамыз

Скаляр кө бейтінді орындасақ    

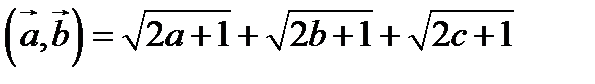
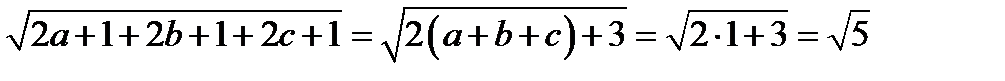
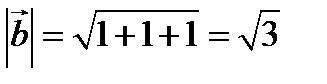
Мына тең сіздік ақ иқ ат 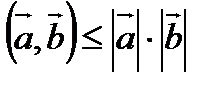 , олай болса  

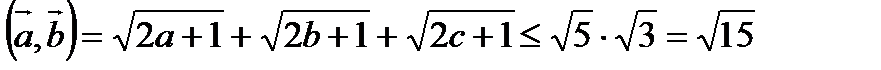
Бұ дан

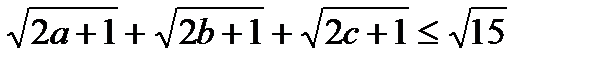
Дә лелдеу керегі де осы еді.

Мысал 12: 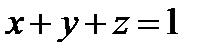 жә не 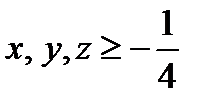 шарттарын қ анағ аттандыратын  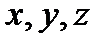сандары ү шін

тең сіздігін дә лелдең із.

Дә лелдеу: Тең сіздікті дә лелдеу ү шін екі векторды қ ұ райық.

Екі вектордың сколяр кө бейтінді 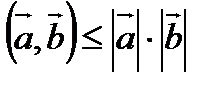  болатынын ескеріп табатынымыз

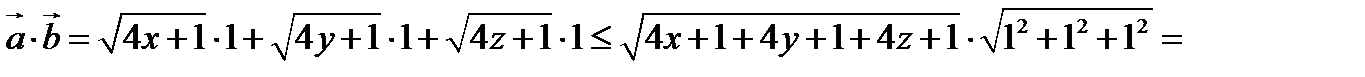
Олай болса

тең сіздігінің дұ рыстығ ын кө руге болады.

Дә лелдеу керегі де осы болатын.

Мысал 13: Тең сіздікті шешің із:

.

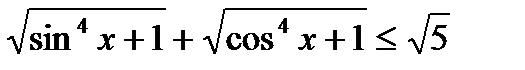Шешуі: Бұ л тең сіздікті вектор қ ұ ру арқ ылы шығ ара алмайтын адамдар ү шін қ иындық туғ ызатыны анық. Векторлар қ ұ ру арқ ылы бұ л тең сіздіктің шешімін жең ілдетуге болады. Олай болса тең сіздіктің типіне сә йкес векторларымызды

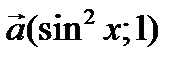 жә не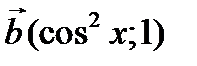

қ ұ рып аламыз. Олай болса

, , ,

                                          .

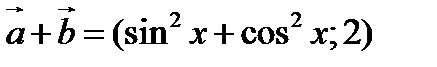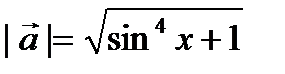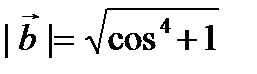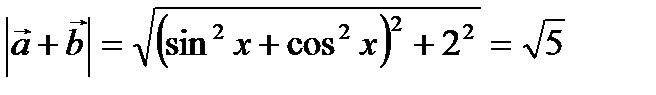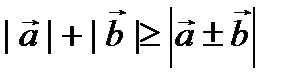 тең сіздіктің ақ иқ ат екендігін білеміз, олай болса:

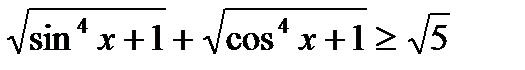
аламыз. Алынғ ан тең сіздікпен бастапқ ы тең сіздіктен

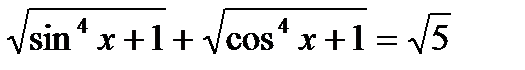
аламыз. Бұ дан 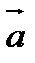 жә не 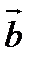 векторлары коллинеар екенін кө реміз.

Демек,

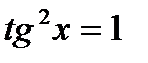                                        ,  жә не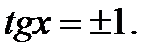

болады. Олай болса 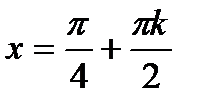, мұ ндағ ы k .                                                                                

Жауабы: , k .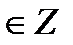          

Мысал 14: Тең сіздікті шешің із:

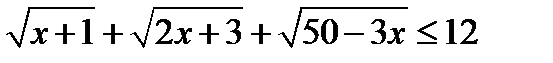
Шешуі: Тең сіздікті шығ армас бұ рын тең сіздіктің мү мкін мә ндер жиынын қ арастырайық:

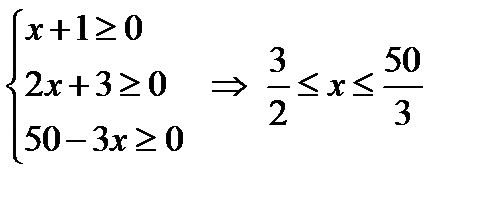
Олай болса берілген тең сіздіктің мү мкін мә ндер жиыны 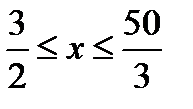  болады.

Енді тең сіздікті шешу ү шін екі векторды қ ұ рып алайық:

Қ ұ рылғ ан екі вектордың скаляр кө бейтіндіс табамыз:

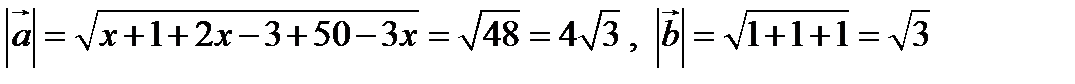
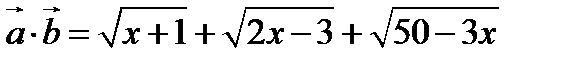
                    Олай болса тең сіздіктің ақ иқ аттығ ын кө реміз

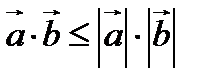
Демек, берілген тең сіздік ө зінің мү мкін мә ндер жиынындағ ы барлық мә нді қ абылдай алады. Берілген тең сіздіктің шеімі

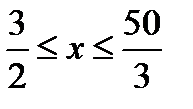
                                                                        Жауабы: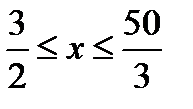

                                                МАЗМҰ НЫ: