2.2 Кейбір теңдеулер жүйесіне векторлар құру арқылы шешімін алу

Тең деулерг жү йесіне векторларды қ ұ ру тә сілі

3. Берілген есепке векторларды қ ұ ру кезінде тең деудің сол жақ бө лігі екі вектордың скаляр кө бейтіндісіне тең болуы қ ажет.

4. Скаляр кө бейтудің нә тижесінде тең деудің оң жақ бө лігінен векторлардың коллинеарлы болуы шарт.

Тең деулер жү йесіне векторлар қ ұ ру арқ ылы шешудің алгоритмі:

7. Ө зіміз жә не векторларын тең деуге қ арап таң дап аламыз;

8. Қ ұ рылғ ан векторлардың ұ зындық тарын жә не скаляр кө бейтіндісін 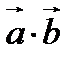табамыз;

9. тең діктің орынды немесе орынсыз болатындығ ын тексереміз

10. Егер тең дік орынды болса, онда тең деудің шешімі бар жә не ол жалғ ыз;

11. Егер тең дік орынды болмай, болса, онда тең деудің шексіз кө п шешімдері болады;

12. Егер тең дік орынды болмай, болса, онда тең деудің шешімдері болмайды.

Векторларды қ ұ ру есеп шығ ару барысында нақ тырақ тү сіндіріледі. Осы ә дісті тең деулер жү йесі ү шін де қ олданып кө рейік

Мысал 6: Тең деулер жү йесін шешің із

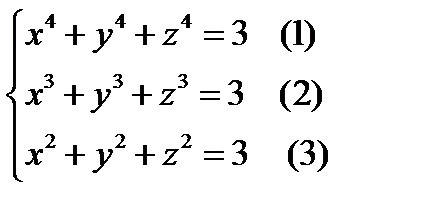
Шешуі: Бұ л тең деулер жү йесін шешу ү шін екі вектор қ ұ рсақ жеткілікті. Векторды қ ұ ру ү шін берілген тең деудің сол жақ бө лігіне жаң а қ ұ рылатын векторлардың координаталары арқ ылы скаляр кө бейтіндісі тең болуын ескереміз. Бұ нда тең деулер жү йесіндегі бір тең деуге векторларды қ ұ рамыз.

Векторларымызды

қ ұ рып алсақ. Енді екі вектордың скаляр кө бейтіндісін табайық:

Екі вектордың коллинеар екенін кө руге болады. Онда

Олай болса бастапқ ы тең деуден (3)

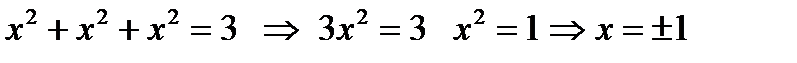
Бірақ 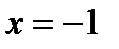тең деудің шешімін қ анағ аттандырмайды. Сондық тан да шешім

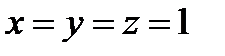
болады.

Жауабы:

Мысал 7: Тең деулер жү йесін шешің із

Векторларымызды

қ ұ рып аламыз. Қ ұ рылғ ан екі вектордың скаляр кө бейтіндісін табайық:

Коши тең сіздігі бойынша

Біз мынадай тең сіздікке келдік . Демек, тең сіздік орынсыз, онда тең деулер жү йесінің шешімі жоқ.

1. Тең деулер жү йесін шешің із:

Шешуі: мұ ндағ ы х≥ 1 жә не у≥ 1 екенін байқ ауғ а болады. Біз векторларымызды

жә не

қ ұ рып алып, екі векторлың скаляр кө бейтіндісін табайық:

жә не

Олай болса, орынды болғ андық тан жә не векторлары коллинеар болады. Демек,

жә не

фукнцияны қ арастырайық. Онда f(x)=f(y) болатынын байқ аймыз. функциясы х≥ 1 болғ анда монотонды ө спелі болады. Олай болса х=у.

Бірінші тең деуіміздің орнына апарып қ ойсақ, онда . Мұ ндағ ы х≥ 1 екенін ескерсек:

Жауабы:

Мысал 8: Тең деулер жү йесін шешің із:

Векторларымызды

қ ұ рып алсақ. Енді екі вектордың скаляр кө бейтіндісін табайық:

Демек, екі вектор коллинеар болады. Олай болса

тең дікті аламыз. Алынғ ан тең дікті тең деулер жү йесіндегі бірінші тең деуге қ ойсақ:

аламыз. Бұ л алынғ ан нә тижені ү шінді тұ рғ ан тең деуге қ ойып, дұ рыстығ ына кө з жеткізуге болады. Олай болса берілген тең деулер жү йесінің шешімі болады.

Жауабы:

Мысал 9: Тең деулер жү йесін шешің із:

Векторларымызды

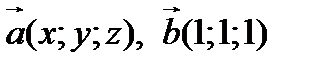
қ ұ рып алсақ. Енді екі вектордың скаляр кө бейтіндісін табамыз:

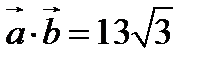
Бұ л жерден болғ андық тан, берілген тең деулер жү йесінің шексіз кө п шешімі болады.

⇐ Предыдущая 1 234 Следующая ⇒