Зміст. Приклади.

Визначник[ред. • ред. код]

Матеріал з Вікіпедії — вільної енциклопедії.

Площа паралелограма є модулем визначника матриці 2× 2 із векторів його сторін.

Визначник або детермінант — вираз складений за певним законом з n² елементів квадратної матриці. Одна з найважливіших характеристикквадратних матриць.

Для квадратної матриці розміру 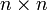визначник є многочленом степеня 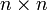від елементів матриці, і є сумою добутків елементів матриці зі всіма можливими комбінаціями різних номерів рядків і стовпців (в кожному із добутків є рівно по одному елементу з кожного рядка і кожного стовпця). Кожному добутку приписується знак плюс чи мінус, в залежності від парності перестановки номерів.

Якщо елементами матриці є числа, то визначник — також число. Взагалі, визначник може бути функціональним або належати якомуськомутативному кільцю, залежно від походження матриці.

З точністю до знака, визначник матриці виражає коефіцієнт, на який множаться 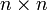-мірні об'єми під дією цієї матриці.

Зміст

[сховати]

· 1 Визначення

o 1. 1 Визначник 2× 2 матриці

o 1. 2 Визначник 3× 3 матриці

· 2 Властивості

· 3 Історія

· 4 Спеціальні види визначників

· 5 Див. також

· 6 Джерела

Визначення[ред. • ред. код]

Визначник матриці 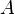задається формулою:

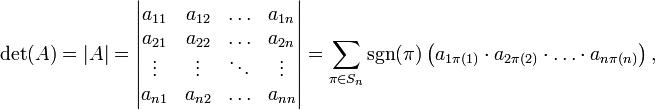
де 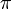— перестановка множини 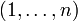і 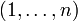це знак (або парність) перестановки, тобто дорівнює 1 чи -1 залежно від парності числа інверсій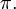

Кількість доданків у сумі дорівнює 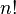і номери рядка та стовпця елементів матриці, що входять у один добуток, не повторюються.

Матриця називається виродженою, якщо її визначник дорівнює нулю, а в іншому випадку невиродженою.

Визначник 2× 2 матриці [ред. • ред. код]

Щоб знайти визначник 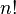матриці, множимо елементи головної діагоналі та віднімаємо добуток елементів побічної діагоналі:

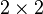
Визначник 3× 3 матриці [ред. • ред. код]

Щоб знайти визначник 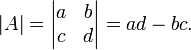матриці, будуємо шість добутків таким чином:

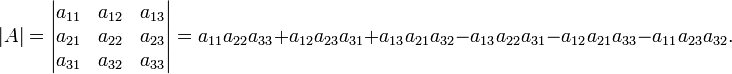
Для знаходження визначників високого порядку застосовуються принципово інші методи (насамперед, метод Гауса), що вимагають значно меншої кількості арифметичних операцій ( 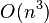замість ).

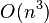Властивості[ред. • ред. код]

1. Якщо помножити якийсь рядок на константу 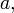то визначник також помножиться на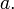

2. Якщо у матриці поміняти місцями будь-які два рядки, то знак визначника зміниться на протилежний.

3. При додаванні до будь-якого рядка лінійної комбінації кількох інших рядків визначник не зміниться.

4. У матриці з двома однаковими/пропорційними рядками або з нульовим рядком, визначник дорівнює нулю.

5. Всі властивості визначників, що стосуються рядків, так само справедливі і для стовпців.

6. Визначник трикутної матриці дорівнює добутку елементів на діагоналі.

7. Теорема Лапласа: визначник квадратної матриці дорівнює сумі добутків елементів деякого рядка на відповідні їм алгебраїчні доповнення.

8. Лема про фальшивий розклад: сума добутків елементів деякого рядка на алгебраїчні доповнення відповідних елементів паралельного рядка дорівнює нулю.

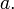
10.

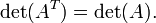
11.

В лінійній алгебрі доводиться, що перші три властивості майже характеризують визначник матриць з елементами у полі. А саме, якщо функція елементів матриці задовольняє 1, 2, 3, то така функція пропорціональна .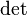

Історія[ред. • ред. код]

Китайський текст «Математика в дев'яти книгах» (написаний ще до нашої ери) містить приклади використання визначника для розв'язання системи рівнянь, ще задовго до введення визначників японським математиком ТакакадзуСекі (1683) та німецьким математиком Лейбніцем (1693).

Одне із найповніших джерел з історії визначників (до початку 20 століття) — це чотирьохтомна хрестоматія Thetheoryofdeterminantsinthehistoricalorderofdevelopment byThomasMuir, NewYork, DoverPublications, 1960. Див. [1]

Приклади.

1) (1. 4)

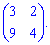
Застосуємо правило обчислення визначника для матриці другого порядку.

2) (1. 6)

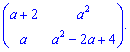
Виконаємо обчислення згідно правила

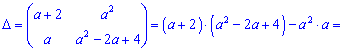
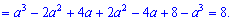
3) (1. 8)

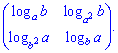
Даний приклад виглядає складним, проте зі знанням наступних правил логарифма

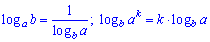
розв'язується напрочуд швидко.

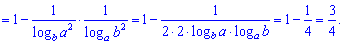
4) (1. 14)

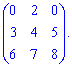
Обчислимо даний визначник двома способами: правилом трикутників та через алгебраїчні доповнення.

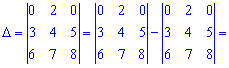
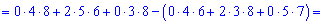
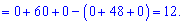
А зараз розкладемо за елементами першого рядка, оскільки в ньому найбільше нулів

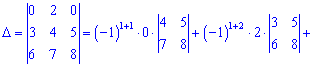
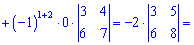
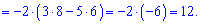
В цьому прикладі спеціально виписані доповнення біля нульових множників, оскільки не всі розуміють звідки беруться доповнення. За правилом вони рівні визначнику, який утворюється викреслюванням рядка 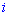та стовпця 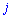того елемента 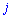, для якого шукаються, помноженому на мінус одиницю в степені

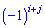Схематично на прикладі матриці четвертого порядку це виглядає так:

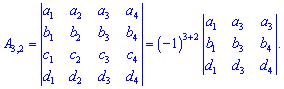
Уважно подивіться, які елементи у визначнику виписані для доповнень і Вам все стане зрозуміло.

Суть методу алгебраїчних доповнень полягає в тому, що коли ми маємо матрицю з нульовими елементами то, розклавши її за за рядком чи стовпцем в якому найбільше нулів нам залишається обчислити стільки визначників на порядок менших від основної матриці, скільки є ненульових елементів. Це значно спрощує обчислення.

6) (1. 19)

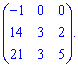
Якщо обчислення проводити за правилом трикутників, то отримаємо багато нульових добутків. В такого роду прикладах доцільно використовувати алгебраїчні доповнення.

7) (1. 21)

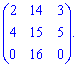
Обчислимо визначник через алгебраїчні доповнення третього рядка

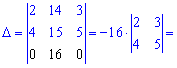
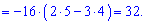
Як можна переконатися, розв'язок з допомогою алгебраїчних доповнень у випадках розріджених матриць можна отримати швико і без великої кількості обчислень.

8) (1. 58)

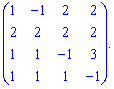
Виконаємо елементарні перетворення. Від другогорядка віднімемо перший, а від четвертого – третій. Отримаємо розріджену матрицю

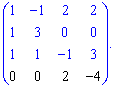
Визначник знайдемо через алгебраїчні доповнення до четвертого рядка

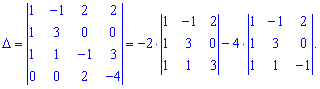
Обчислимо кожен з доданків

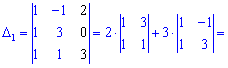
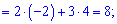
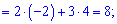
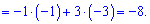
Підставляємо у визначник

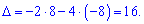
9) (1. 72)

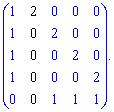
Знайдемо визначник через розклад за рядками і стовпцями, що містять нулі (виділені чорним).

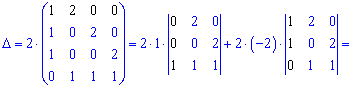
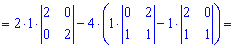
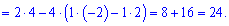
Таким методом знаходження визначника п'ятого порядку звелося до простих обчислень. Практикуйте та вчіть правила і через деякий час у Вас виходитиме не гірше. До зустрічі в наступних уроках!

----------------------------------------------

⇐ Предыдущая 123 Следующая ⇒