Доказательство. Д оказательство. Доказательство

⇐ ПредыдущаяСтр 2 из 5Следующая ⇒

Доказательство

Очевидно, 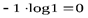. Для остальных вероятностей рассмотрим предел

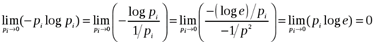т. е. 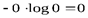, что в сумме для п вероятностей даст нуль.

Свойство 4. Всякое изменение вероятностей 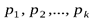в сторону их выравнивания увеличивает энтропию .

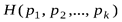Д оказательство

Энтропия исходных вероятностей равна .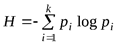

Пусть 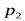> 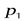, тогда 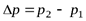. После выравнивания 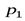и 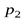получим, + +…+ .

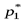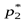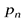
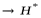Нам нужно доказать, что 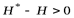. Рассмотрим

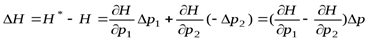где 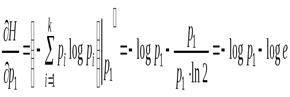и

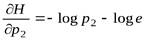. Тогда 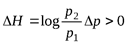, так как 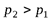, что и требовалось доказать.

Свойство 5. Энтропия максимальна, когда все исходы опыта равновероятны.

Доказательство

На 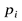существует ограничение .

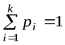Найдем локальный экстремум. Для этого рассмотрим функционал

, Где коэффициент по Лагранжу, а – из условия ограничения.

Берем первые частные производные по :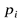

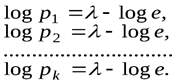
Поскольку правые части всех выражений одинаковые, можно сделать вывод о равновероятных состояниях исходов опыта, то есть:

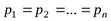Тогда .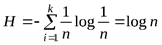

Получили выражение для максимальной энтропии, соответствующее формуле Хартли.

Иными словами, среди всех опытов, имеющих k исходов, наиболее неопределенным является опыт с распределением вероятностей:

Исходы опыта	А₁	А₂	А₃	…	А_k
Вероятности				…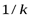

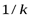
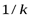
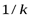
И функция 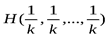растет с увеличением числа k (см. аксиому 3). Причем,

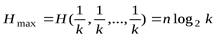. (1. 5)

Для одного же исхода опыта 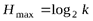. Например это может касаться k букв алфавита при равновероятном их использовании. Энтропия появления одной буквы будет равна 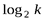, а трех последовательно .

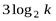Свойство 6. Функция 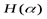удовлетворяет соотношению

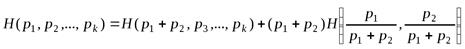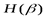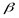Это соотношение означает, что неопределенность опыта с распределением вероятностей

Исходы опыта	B	A₃	…	A_k
Вероятности		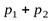p₃	…	p_k

получаемого отождествлением двух первых исходов опыта 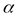, меньше неопределенности 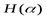этого последнего опыта на умноженную на 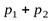меру неопределенности опыта 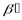, состоящего в выяснении того, какой именно из первых двух исходов опыта 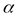имел место, если известно, что осуществился один из именно этих двух исходов.

Свойство 7. Математическое ожидание информации есть энтропия (без доказательства)

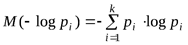Пример 1. Пусть из многолетних наблюдений за погодой известно, что для определенного пункта вероятность того, что 15 июня будет идти дождь, равна 0, 4, а вероятность того, что в указанный день дождя не будет, равна 0, 6. пусть далее для этого же пункта вероятность того, что 15 ноябрябудет идти дождь равна 0, 65, вероятность того, что 15 ноября будет идти снег, равна 0, 15 и вероятность того, что 15 ноября вовсе не будет осадков, равна 0, 2. Если из всех характеристик погоды интересоваться лишь вопросом о наличии и о характере осадков, то в какой из двух перечисленных дней погоду в рассматриваемом пункте следует считать более неопределенной?

Решение

Согласно тому, как понимается здесь слово «погода», опыта 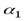и 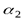, состоящие в выяснении того, какая погода имела место 15 июня и 15 ноября, характеризуются следующими таблицами вероятностей:

опыт :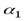

исходы опыта	дождь	отсутствие осадков
вероятность	0, 4	0, 6

опыт :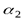

исходы опыта	дождь	снег	отсутствие осадков
вероятность	0, 65	0, 15	0, 2

Поэтому энтропии наших двух опытов равны

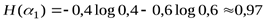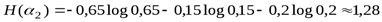бита,

бита .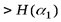

Следовательно, погоду 15 ноября в рассматриваемом пункте следует считать более неопределенной, чем 15 июня.

Полученный результат, разумеется, существенно зависит от того, как понимать слово «погода»; без точного разъяснения того, что под этим понимается, наша задача вообще не имеет смысла. В частности, если интересоваться только тем, будут ли в рассматриваемый день осадки или нет, то исходы «дождь» и «снег» опыта 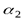следует объединить. При этом вместо 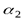мы будем иметь опыт 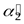, энтропия которого равна

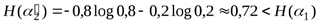Поэтому при таком понимании погоды надо считать, что 15 ноября погода является менее неопределенной, чем 15 июня. Если же интересоваться не только осадками, но и, например, температурой воздуха, то решение задачи становится более сложным и требует привлечения дополнительных данных о распределении значений температуры в рассматриваемом пункте 15 июня и 15 ноября.

Соображения, развитые в решении этой задачи, представляют интерес для оценки качества предсказания погоды по тому или иному методу (аналогично обстоит дело и в случае любого другого прогноза). В самом деле, при оценке качества прогноза нельзя учитывать лишь его точность (т. е. процент случаев, в которых прогноз оправдывается); иначе нам пришлось бы высоко оценивать любой прогноз, имеющий большие шансы оказаться правильным. В том числе, например, и предсказание отсутствия снега в Киеве 1 июня, не представляющее, разумеется, никакой ценности. При сравнении качества различных прогнозов следует учитывать не только их точность, но и трудность удачного прогноза, которую можно характеризовать степенью неопределенности соответствующего опыта.

Пример 2. Найти энтропию непрерывной случайной величины, распределенной по показательному закону

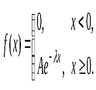Решение

Применяя одно из свойств плотности распределения, находим 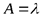. Таким образом, по формуле (1. 4)

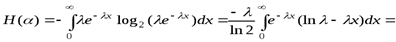
[применяя формулу интегрирования по частям, получаем]

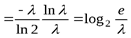бит.

Пример 3. Сравнить неопределенность, приходящуюся на каждую букву источника информации русского языка и характеризующуюся ансамблем, представленным в таблице (знаком «–» обозначен промежуток между словами), с неопределенностью того же источника, но при равновероятном использовании букв.

Буква	Вероятность	Буква	Вероят- ность	Буква	Вероят- ность	Буква	Вероят- ность
а	0, 064	и	0, 064	р	0, 041	ш	0, 006
б	0, 015	й	0, 010	с	0, 047	щ	0, 003
в	0, 039	к	0, 029	т	0, 056	ъ, ь	0, 015
г	0, 014	л	0, 036	у	0, 021	ы	0, 016
д	0, 026	м	0, 026	ф	0, 002	э	0, 003
е, ё	0, 074	н	0, 056	х	0, 009	ю	0, 007
ж	0, 008	о	0, 096	ц	0, 004	я	0, 19
з	0, 015	п	0, 024	ч	0, 013	–	0, 142

Решение

При одинаковых вероятностях появления всех 32 (считая промежутки между словами и буквы е, ё и ъ, ь за одну букву) букв алфавита неопределенность, приходящаяся на одну букву, равна (см. формулу (1. 5)):

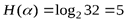бит.

Энтропия источника, характеризующегося вышеуказанной таблицей, находится по формуле (1. 3):

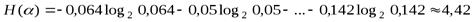бит.

Таким образом, неравномерность распределения вероятностей использования букв снижает энтропию источника с 5 до 4, 42 бит.

Пример 4. Определить энтропию сообщения, состоящего из 5 букв, если общее число букв в алфавите равно 32 и все пятибуквенные сообщения равновероятны.

Решение

Общее число пятибуквенных сообщений .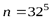

Используя (1. 5), получаем:

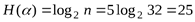бит.

Пример 5. Заданы ансамбли U и V двух дискретных случайных величин :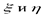

	0, 5	0, 7	0, 9	0, 3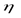
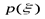
	0, 25	0, 25	0, 25	0, 25		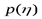	0, 25	0, 25	0, 25	0, 25

Сравните их энтропии.

Решение

+Поскольку энтропия не зависит от конкретных значений случайной величины, а вероятности их появления у 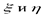одинаковы, то

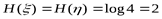бит.

1. 5. Энтропия сложных событий. Условная энтропия

Мера неопределенности, используемая в решении задач, касающихся работы линий связи, например, должна быть приспособлена, в первую очередь, для оценки степени неопределенности сложных «составных событий», состоящих из целой совокупности следующих друг за другом испытаний.

Пусть 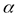и 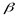– два независимых опыта с распределениями вероятностей:

опыт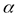

исходы опыта	A₁	A₂	…	A_k
вероятности	p(A₁)	p(A₂)	…	p(A_k)

опыт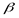

исходы опыта	B₁	B₂	…	B_l
вероятности	p(B₁)	p(B₂)	…	p(B_l)

Рассмотрим сложный опыт 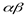, состоящий в том, что одновременно осуществляются опыта 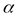и 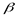. Этот опыт может иметь kl исходов:

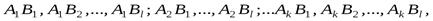
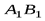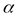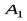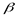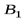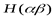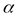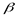где, например, означает, что опыт имел исход , а опыт – исход . Элементарно доказывается согласно определению с учетом того, что и независимы и 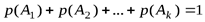, правило сложения энтропий

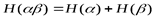. (1. 6)

Это правило распространяется и на большее количество независимых величин.

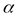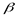Если задана матрица вероятностей объединения двух исходов опытов и , то

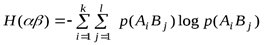, (1. 7)

где 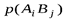– вероятность совместного появления событий .

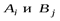Если опыты 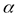и 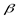не независимы, энтропия сложного опыта 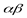в общем случае равна

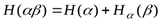. (1. 8)

где 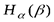–полная условная или просто условная энтропия опыта 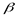относительно ансамбля :

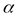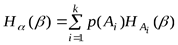
и

.

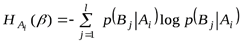Величину 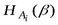называют частной условной энтропией опыта 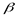. 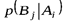– вероятность реализации исхода 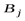, опыта 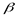при условии, что реализовался исход 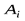опыта 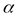. Иначе можно записать:

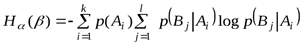(1. 9)

Таким образом, энтропия объединения двух статистически связанных опытов 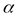и 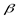равняется безусловной энтропии одного опыта плюс условная энтропия другого относительно первого.

Для объединения любого числа зависимых опытов:

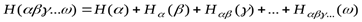(1. 10)

Укажем некоторые важнейшие свойства величины .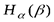

1. Очевидно, что это есть неотрицательное число. Кроме того,

.

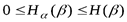Таким образом, случаи, когда исход опыта 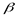полностью определяется исходом 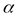и когда опыта 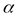и 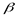независимы, являются в определенном смысле крайними.

2. Если все вероятности 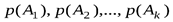отличны от нуля, т. е. если опыт 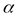имеет действительно k исходов, то 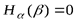в том и только в том случае, если 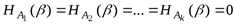, т. е. если при любом исходе опыта 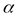результат опыта 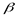становится полностью определенным (тривиальным образом это условие выполняется в том случае, если опыт 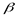с самого начала не является неопределенным). При этом мы имеем

.

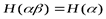3. Если же опыта 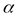и 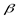являются независимыми, то

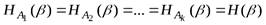и .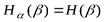

4. Так как сложные опыты 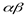и 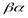не отличаются одно от другого, то

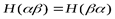, т. е. .

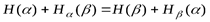Отсюда следует, в частности, что, зная энтропи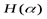и и 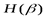опытов 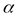и и 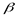условную энтропию 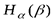опыта 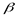при условии выполнения 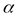, мы можем определить также и условную энтропию 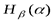опыта 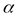при условии выполнения :

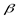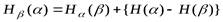. (1. 11)

5. Поскольку 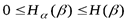, то из формулы (3. 9) следует, что

;

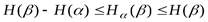при 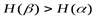эта оценка величины условной энтропии 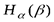оказывается более точной. Равенство

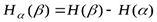
имеет место при 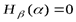, т. е. если исход опыта 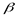полностью определяет исход опыта 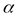; при этом всегда будет .

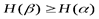Пример 1. Определить энтропии 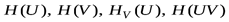, если задана матрица вероятностей исходов опытов :

.

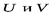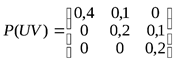Решение

Вычислим безусловные вероятности исходов каждого опыта как суммы общих вероятностей по строкам и столбцам заданной матрицы: , .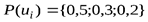

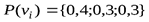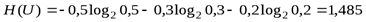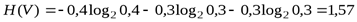бит.

бит.

Находим условные вероятности (чтобы воспользоваться формулой (1. 9)) :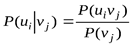

; ;

; .

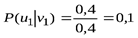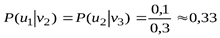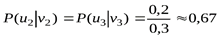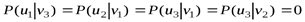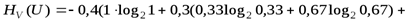
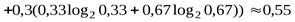бит.

По формуле (1. 7) получаем:

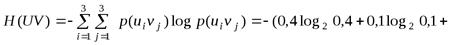
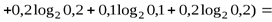
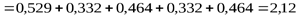бит.

По формуле (1. 8) можно проверить результаты вычислений:

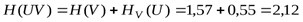бит.

Пример 2. Известны энтропии двух зависимых источников: 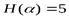бит, 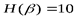бит. Определить в каких границах будет изменяться условная энтропия 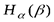при изменении 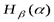в максимально возможных границах.

Р 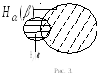ешение

+При решении удобно использовать графическое представление связи между энтропиями. Из рисунка 3 видим, что максимального значения 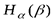достигает при отсутствии взаимосвязи, и будет равняться 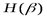, то есть 10 бит. По мере увеличения взаимосвязи 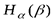будет уменьшаться до значения 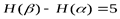бит. При этом .

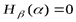Также можно определить энтропию случайной величины, введя предварительно понятия распределения случайной величины 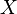, имеющей конечное число значений: ^[2]

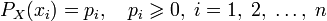
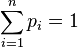
и собственной информации:

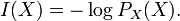
Тогда энтропия определяется как:

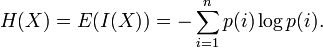
От количества возможных состояний случайной величины 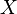зависит единица измерения количества информации и энтропии: бит, нат, трит или хартли.
От основания логарифма зависит числовая величина единицы измерения количества информации и энтропии.

Энтропия является количеством, определённым в контексте вероятностной модели для источника данных. Например, кидание монеты имеет энтропию:

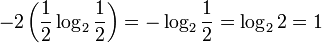бит на одно кидание (при условии его независимости), а количество возможных состояний равно: 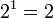возможных состояния (значения) (" орёл" и " решка" ).

У источника, который генерирует строку, состоящую только из букв «А», энтропия равна нулю: 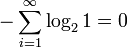, а количество возможных состояний равно: 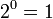возможное состояние (значение) («А») и от основания логарифма не зависит.
Это тоже информация, которую тоже надо учитывать. Примером запоминающих устройств в которых используются разряды с энтропией равной нулю, но с количеством информации равным 1 возможному состоянию, т. е. не равным нулю, являются разряды данных записанных в ПЗУ, в которых каждый разряд имеет только одно возможное состояние.

Так, например, опытным путём можно установить, что энтропия английского текста равна 1, 5 бит на символ, что конечно будет варьироваться для разных текстов. Степень энтропии источника данных означает среднее число битов на элемент данных, требуемых для её зашифровки без потери информации, при оптимальном кодировании.

1. Некоторые биты данных могут не нести информации. Например, структуры данных часто хранят избыточную информацию, или имеют идентичные секции независимо от информации в структуре данных.

2. Количество энтропии не всегда выражается целым числом битов.

⇐ Предыдущая 123 4 5 Следующая ⇒