Доказательство

Энтропия

1. 1. Комбинаторный подход к вычислению количества информации. Формула Хартли

Обозначим через Iколичество информации, n – число состояний физической системы, тогда I = I(n) – функция количества информации. И повторим рассуждения Р. Хартли, позволившие ему получить меру количества информации. Предварительно примем, что информация – это устраненная неопределенность.

Предположим, что какое-то событие имеет m равновероятных исходов. Таким событием может быть, например, появление любого символа из алфавита, содержащего m таких символов. Как измерить количество информации, которое может быть передано при помощи такого алфавита? Это можно сделать, определив число N возможных комбинаций букв алфавита, то есть число возможных сообщений, которые могут быть переданы при помощи этого алфавита. Если сообщение формируется из одного символа, то N = m, если из двух, то N = m². Если сообщение содержит n символов (n – длина сообщения), то N = mⁿ. Казалось бы, искомая мера количества информации найдена. Ее можно понимать как меру неопределенности исхода опыта, если под событием подразумевать случайный выбор какого-либо сообщения из некоторого числа возможных. Однако эта мера не совсем удобна. При наличии алфавита, состоящего из одного символа, т. е. когда m = 1, возможно появление только этого символа. Следовательно, неопределенности в этом случае не существует, и появление этого символа не несет никакой информации. Между тем, значение N при m = 1 не обращается в нуль. Для двух независимых источников сообщений (или алфавита) с N₁ и N₂ числом возможных сообщений общее число возможных сообщений 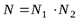, в то время как логичнее было бы считать, что количество информации, получаемое от двух независимых источников, должно быть не произведением, а суммой составляющих величин.

Выход из положения Р. Хартли увидел том, чтобы информацию I, приходящуюся на одно сообщение, определять логарифмом общего числа возможных сообщений N:

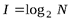. (1. 1)

Формула Хартли позволяет определить количество информации в сообщении только для случая, когда появление символов равновероятно и они статистически независимы.

+На практике же условия позволяющие определить количество информации по (1. 1) выполняются редко. При определении количества информации необходимо учитывать не только количество разнообразных сообщений, которые можно получить от источника, но и вероятность их получения.

Вывод формулы Шеннона

Рассмотрим ряд чисел 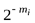, где i = 1,.., n, а m_i – целые положительные числа, такие что .

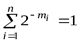Для кодового слова длиной m_i меру неопределенности закодированного состояния можно представить в виде:

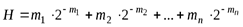Для примера, приведенного в таблице, мера неопределенности будет равна:

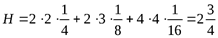
– среднее количество знаков в кодовом слове (математическое ожидание).

Если взять не двоичную систему счисления, а систему счисления с основанием a, то для ряда чисел 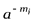, закодированных кодовыми словами длиной m_i меру неопределенности закодированного состояния можно представить в виде:

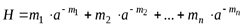Если опять обратимся к таблице, то увидим, что 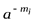– это вероятность состояния, закодированного кодовым словом длиной m_i, то есть p_i. При этом .

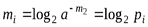Поэтому, выражение для неопределенности (1. 1) Шеннон записал, объединив формулу для любой системы счисления и получил:

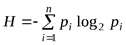назвав это выражение энтропией. На самом деле впервые функция энтропии была введена в термодинамику Р. Клаузиусом (термин «энтропия» был введен тоже Клаузиусом, образовавшим его от корня греческого слова «тропе», означающего «превращение» с добавлением заимствованной из слова «энергия» приставки «эн-»), усовершенствована Л. Больцманом и наконец М. Планком. Уже в этом виде ее применил Клод Шеннон.

То есть, в самом общем случае, на вероятностном языке дляопыта 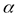стаблицейвероятностей

исходы опыта	А₁	А₂	А₃	…	А_k
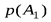
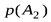
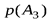
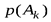
вероятности				…		(1. 2)

меранеопределенностиравна

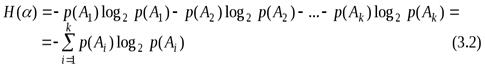и называется энтропией опыта 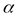(или дискретного распределения (1. 2). Напомним, что .

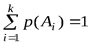Итак, энтропия – это среднее количество информации, приходящееся на один исход опыта (для дискретных систем).

Аналогичная (1. 3) формула имеет место и при 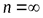в предположении сходимости соответствующего ряда.

Наряду с энтропией дискретного распределения рассматривается также и энтропия непрерывной случайной величины, которая определяется формулой

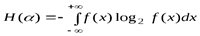, (1. 4)

где 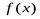– плотность распределения вероятностей. В предположении сходимости интеграл (1. 4) является мерой неопределенности непрерывной случайной величины.

1. 3. Единицы измерения энтропии и информации

Итак, исторически первые шаги к введению понятия энтропии были сделаны еще в 1928 г. американским инженером-связистом Р. Хартли, предложившим характеризовать степень неопределенности опыта с k различными исходами числом log k. Замерунеопределенностиопыта, имеющего k равновероятныхисходов, приняли число 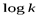. В конкретных применениях «меры степени неопределенности» обычно используются логарифмы при основании два. Это означает, что за единицу измерения степени неопределенности здесь принимается неопределенность, содержащаяся в событии, имеющем два равновероятных исхода (например, в событии, состоящем в подбрасывании идеальной монеты). Такая единица измерения неопределенности называется двоичной единицей или битом (bit образовано из двух начальных и последней букв английского выражения binary unit, что значит двоичная единица). Таким образом, запись 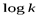(где не указано основание логарифма) будет обычно означать .

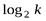+Кроме того, используется дит – это энтропия системы с десятью равновероятными состояниями, вычисленная с помощью логарифма с основанием десять. Иногда бурт физическую систему с е состояниями, тогда натуральную единицу количества информации называют нитом, при этом основание логарифма в формуле Шеннона равно е.

Взаимосвязь между единицами количества информации:

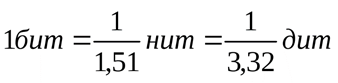
С точки зрения теории кодирования существует объяснение, почему используется двоичная система (основание логарифма).

Число букв в алфавите	Число разрядов в кодовом слове	Мощность




…	…	…

…	…	…

Как видим, оптимальное количество букв в алфавите находится между 3 и 4. То есть, лучшей была бы троичная система, но ее труднее реализовать.

Двоичная система, так же как и четверичная – почти оптимальные. Но легче реализовать двоичную систему.

1. 4. Свойства функции энтропии

Свойство 1. Энтропия не может принимать отрицательных значений.

Доказательство

Так как всегда 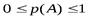, то 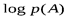не может быть положительным, а 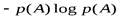– отрицательным.

Свойство 2. Функция 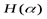при очень малом изменении вероятностей 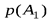, …, 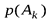изменится очень мало.

К омментарий. На рис. 1 изображен график функции 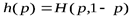, показывающий, как меняется энтропия 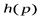при изменениирот0 до 1.

Д ля того чтобы представить себе характер зависимости функции 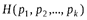от отдельных вероятностей 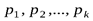, рассмотрим более внимательно график функции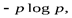 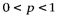(см. рис. 2). Из этого графика видно, что при 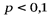величина 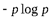растет чрезвычайно быстро; поэтому в этой области сравнительно небольшому уменьшению вероятности 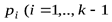или k) отвечает очень значительное уменьшение соответствующего слагаемого 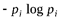в выражении функции 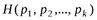. Это приводит к тому, что обычно слагаемые 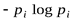, отвечающие очень малым значениям вероятности 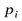, вносят много меньший вклад в выражение 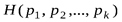, чем прочие члены, так что при вычислении энтропии сравнительно маловероятные исходы часто можно без большой ошибки просто опустить. Наоборот, в области между 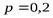и 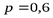, где функция 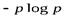принимает наибольшие значения, она меняется сравнительно плавно; поэтому в этой области даже довольно значительное изменение вероятностей 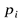сравнительно мало отражается на величине энтропии.

Свойство 3. Энтропия равна нулю:

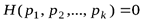если вероятность одного из исходов опыта равна 1, а остальные равны нулю. Т. е. энтропия равна нулю, если возможен только один исход опыта (с вероятностью равной единице).

12 3 4 5 Следующая ⇒