2 4-сыныпта теңдеуді оқыту әдістемесі

2 4-сыныпта тең деуді оқ ыту ә дістемесі

2. 1 Тең деулерді оқ ытудың ә дістемесі

Бастауыш мектепте математикалық білімдер жү йесін оқ ытуда тең деудің орны ерекше. Тең деуді терең тү сініп мең геру математикалық білімдерді одан ә рі дамытуғ а, қ оршағ ан ортадағ ы сан алуан қ ұ былыстарғ а, терең мағ ыналы модельдер жасауғ а ү йретеді. Тең деулерді шешу оқ ушыларды ең бек сү йгіштікке тә рбиелейді. Қ арастырылатын мә селерді ең тиімді, ұ тымды, пайдалы жақ тарынан зерттеуге ү йретеді. Атқ арылатын жұ мыстарғ а терең, салыстырмалы тү рде жан–жақ ты талдаулар жасай отырып, дұ рыс жоспар қ ұ руғ а пә рменді кө мегін тигізеді. Орындалғ ан жұ мыстардың нә тижелеріне сыншыл кө зқ араспен қ орытындылар жасауғ а ү йретеді. Оқ ушылардың ойлау жү йесінің, ой қ орытындыларының ұ тымды логикалық жолымен дамуына кең жол салады. Олай болса, тең деулерді шешуі мектеп математикасын басқ а салалары сияқ ты, оқ ушылардың ойлау жү йесінің жас жеткіншектерге лайық ты дамуына, оларды қ оғ амғ а, Отанына пайдалы азамат болып қ алыптасуына лайық ты пайдасын тигізеді.

Тең деу деп қ ұ рамында ә ріп болатын жә не онымен белгіленген санды іздеу мақ саты қ ойылатын тең дікті айтады. Белгісіз санның тең деуді тура санды тең дікке айналдыратын мә нін тең деудің тү бірі деп атайды.
Тең деуді шешу дегеніміз оның тү бірлерін табу. Тең деу ұ ғ ымы қ ұ рамында ә ріпті ө рнегі (немесе ә рпі) бар тең дік ретінде 1-ші сыныпта енгізіледі
а+2=8 8-а=6 а-2=4 – бұ лар тең деулер. Оқ ушыларғ а тең деу болу ү шін, ә ріпті ө рнек пен ө рнектің мә ні арасында тең дік таң басы болу керектігі туралы тү сіндіріледі. Тең деудің сол жақ жә не оң жақ бө лігі болады.

Тең деу алгебралық ұ ғ ым ретінде ө зінің пайда болуы жө нінен негізгі ү ш бө лікке бө лінеді:

- тең деу мазмұ нды есептер шешу қ ұ ралы;

-тең деу алгебралық элементтерді ү йретуге қ ызмет ететін ерекше формуланың ролін атқ арады;

-тең деу формула ретінде қ осымша санды немесе ө зінің шешімі болатын нү ктенің координатасын анық тайды.

Сонымен, тең деу кө п аспектілі жалпы математикалық ұ ғ ым. Математикалық білім беру ісінде ешбір аспектіні қ алдыруғ а болмайды.

Тең деумен танысу дерексіз сандармен берілген есептерді шығ арғ анда болады, мысалы мынадай: «Белгісіз санғ а 3-ті қ осып, 8 алғ ан. Белгісіз санды табу керек». Осы есеп бойынша белгісіз саны бар мысал қ ұ растырылады, оны былай жазуғ а болады +3=8. Содан кейін мұ ғ алім математикадан белгісіз сан латын ә ріптерімен белгіленеді деп тү сіндіреді. Бір ә ріптің мысалы х (икс) ә рпінің жазылуы жә не оқ ылуы беріледі. Белгісіз санды ә ріппен белгілеу жә не мысалды оқ у ұ сынылады. Мынадай мысалдарды шығ аруды ү йрену мақ саты қ ойылады.

М ұ ғ а л і м. Белгісіз санғ а 3-ті қ осқ анда қ анша шық са, сонша дө ң гелекті алып қ ойың дар. Қ анша дө ң гелекті алып қ ойдың дар?

О қ у ш ы. 8 дө ң гелек.

М ұ ғ а л і м. 8 санын қ алай алдың дар?

О қ у ш ы. Белгісіз санғ а 3-ті қ остық.

Мұ ғ ал і м. Белгісіз дө ң гелектер санын қ осқ ан 3 дө ң гелекті кө рсетің дер. Бұ л 3 дө ң гелекті ә рі ысырып қ ойың дар. Ә уелі қ анша дө ң гелек бар еді?

О қ у ш ы. 5 дө ң гелек.

М ұ ғ а л і м. Қ анша дө ң гелек болғ анын қ алай білдің дер?

О қ у ш ы. Барлық дө ң гелектен 3 дө ң гелекті шегердік..

М ұ ғ а л і м. мысалғ а қ арап, не білгендерің ді айтың дар.

О қ у ш ы. Бірінші қ осылғ ышты білдік.

М ұ ғ а л і м. Бірінші қ осылғ ышты қ алай таптың дар?

О қ у ш ы. 8 қ осындысынан екінші 3 қ осылғ ышты шегердік.

Мұ ғ алім тақ тағ а, ал оқ ушылар дә птерлеріне мынаны жазды:

х+3=8

х=8-3

х=5

Осылайша бірінші немесе екінші қ осылғ ышы белгісіз бірнеше мысал қ арастырады. Мұ ғ алім мұ ндай мысалдар тең деулер деп аталатындығ ынбелгісіз санды табу ү шін – тең деулер шешу керек екендігін тү сініреді. Тең деуді жә не тең деудің тү бірін анық тау бастауыш сыныптарда берілмейді. Оқ ушылар тең деулерді оқ у, жазу жә не шешуге жаттығ ады. Оқ удың тү рлі формаларын кө рсетеді: «9 шығ у ү шін қ андай санғ а 2-ні қ осу керек? », «бірінші қ осылғ ыш 4, екіншісі белгісіз, қ осынды 7-ге тең; екінші 7-ге тең; екінші қ осылғ ыш неге тең? » Бірінші тең деулерді шығ арғ анда балалар жиындарғ а қ олданылатын операцияларғ а, санның қ ұ рамы туралы білімге, қ осынды мен қ осылғ ыштар арасындағ ы қ атынасты тү сінуге (ә р қ осылғ ыш қ осындыдан кем болады) сү йенеді. Біртіндеп оқ ушылар белгісіз қ осылғ ышты табу ережесін игеретін болады, сө йтіп алдың ғ ы уақ ытта оны тең деулерді шешкенде пйдаланады. Содан кейін тең деулердің кө мегімен белгісіз қ осылғ ышты табуғ а арналғ ан сө збен берілген есептерді шығ арады.

Компоненттерінің бірі белгісіз саны бар ө рнек болып келген тең деулер кү рдерілек болып табылады, мысалы: (х+8)-13=15, 70+(40-х) =96 т. с. с. ө йткені осындай қ ұ рлымдағ ы тең деулерді шешкенде белгісіз компоненттерді табу ережесін екі рет қ олдану керек болады. Мысалы, сабақ та (12-х)+10=18 тең деуін қ арастырады.

Мұ ғ алім. Мынадай тең деуді шығ аруды ү йренеміз. Оны дұ рыс оқ удың маң ызы зор. Сол жақ тағ ы ө рнекте қ ай амал ең соң ынан орындалады?

О қ у ш ы. Соң ғ ы амал – қ осу амалы.

М ұ ғ а л і м. Қ осқ анда сандар қ алай аталатын естерің е тү сірің дер жә не бұ л тең деуді оқ ың дар.

О қ у ш ы. Бірінші қ осылғ ыш 12 мен х сандарының айырмасымен ө рнектелген, екінші қ осылғ ыш 10, қ осынды 18.

М ұ ғ а л і м. («қ осылғ ыш», «қ осынды» деген терминдер жазылғ ан таблицаларды қ ыстырып қ ояды). Белгісіз сан қ айсысына енеді?

О қ у ш ы. Бірінші қ осылғ ышқ а.

М ұ ғ а л і м. Бірінші қ осылғ ышты қ алай табу керек?

О қ у ш ы. Бірінші қ осылғ ышты табу ү шін, қ осындыдан екінші қ осылғ ышты шегеру керек (оқ ушы тақ тағ а 12-х=18-10 деп жазады; қ алғ ан барлық оқ ушылар дә птерлеріне жазады).

М ұ ғ а л і м. Біз мұ ндай тең деуді шешкенбіз. Енді біз айырманың мә нін табу ү шін не істейміз?

О қ у ш ы. 18 бен 10 сандарының айырмасын есептеп шығ ару керек (12-х=18-10 деп жазады).

М ұ ғ а л і м. Мұ нда не белгісіз жә не бұ л белгісіз санды қ алай табуғ а болады? Ө з беттерінше шығ арың дар. Х-тің мә нін дұ рыс тапқ ан-таппағ андарын тексеру керек. Ол ү шін не істеу керек?

О қ у ш ы. Х-тің орнына мә ні 4-ті қ ою керек (12-4)+10 деп жазады, есептеп шығ арып (18-ді жазады), оны оң жақ тағ ы санмен салыстыру керек (18=18 деп жазады).

Бұ дан кейін осылайша 36-(20+х) =10 тең деуді қ арастырылады.

1-2-сыныпта шамамен х-2=8, 10-х=4 тү ріндегі, ал 3-сыныпта х·3=12, 5·х=10, 6: х=3 тү ріндегі тең деулер енгізіледі, олар амалдар нә тижелері мен компоненттері арасындағ ы байланыс негізнде шығ арылады.

4-сыныпта (м-4, 83-б. ) х: (52+48)=2, (х-80): 40=64, 327-20: х=323, х-80=640: 40, 1200× х=800× 30 тү ріндегі жә не амалдардың белгісіз компоненттерін табуғ а берілген (149-б. ) кү рделі тең деулер қ арастырылады.

327-20: х=323 кү рделі тең деуін шығ ару ә дістемесі

327-20: х=323

327- =323

20: х=327-323

20: х=4

х=20: 4

х=5

327-20: 5=323

Математика 4-сынып. Амалдардың белгісіз компоненттерін табуғ а берілген (149-б. ) кү рделі тең деулер:

Қ осылғ ыш
Қ осылғ ыш
Қ осындының мә ні

Азайғ ыш
Азайтқ ыш
Айырманың мә ні

Кө бейткіш
Кө бейткіш
Кө бейтіндінің мә ні

Бө лінгіш
Бө лгіш
Бө ліндінің мә ні

Тең деуді шешу

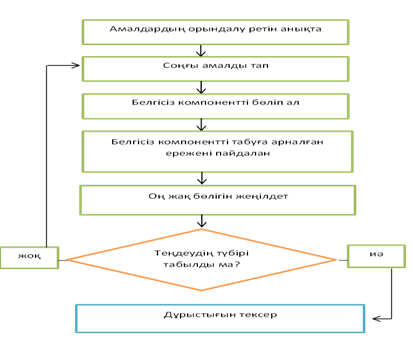
Осы тү рдегі тең деуді шешуге ү йрету ө рнекке талдау жасауғ а ұ зақ уақ ыт жаттығ уды жә не белгісіз компоненттерді табу ережесі туралы жақ сы білімді талап етеді. Алғ ашқ ыда шешілген тең деулерді тү сіндіру жаттығ уын жү ргізген пайдалы. Сонымен қ атар берілген тең деуді шешу ү шін онда не белгісіз жә не оны шешу ү шін қ андай ережелерді еске тү сіру керектігін алдын ала анық тайтын тең деулерді жирек шешу керек болады. Мұ ндай жұ мыс қ атені болдырмайды жә не қ атені болдырмайды жә не тең деулерді шеше білуге кө мектеседі.

Тең деумен танысқ аннан кейін оқ ушыларда оларды шешу білігі қ алыптасады.

Тең деуді шешу – ол тең деуді тура тең дікке айналдыратындай, а ә рпінің мә ндерін табу деген сө з. Оқ ушыларды тең деудің ә ртү рлі тә сілдерімен таныстыру қ ажет. Тең деулерді тү сіндіруде мынадай анық тама беріледі: «Тең деу – оның қ ұ рамына енетін ө рнектің мә нін табуды қ ажет ететін тең дік».

Тең деу жайында тү сінік қ алыптастыру жә не оны шешуді ү йретудің ә дістемелік негіздері екі бағ ыттағ ы мә селені қ амтиды. Оның біріншісі – тең деуді предикат ретінде анық тау. Ә рине мұ нда қ ысқ а тү рде тұ жырымдалғ ан формалары логикалық анық тама берілмейді. Тең деу ұ ғ ымының мә н-мағ ынасы контестік ә діспен ашылады. Сонда тең деудің қ ұ рамында ә ріп яғ ни айнымалы бар, тең дік, айнымалының оны тура санды тең дікке айналдыратын мә ні іздеу керек мақ саты қ ойылады, сондай мә ні табылса, ол тең деудің шешімі, яғ ни тү бірі болып табылады.
Тең деу ұ ғ ымының мә н-мағ ынасын ашуда жоғ арығ ыдай тү сініктеме келтіру, оны шешудің «сынап кө ру» «яғ ни іріктеп алу немесе таң дап алу» деп аталатын тә сілін анық тайды.

Осығ ан бірнеше мысал келтірейік:
1. x+2=8 (қ андай санғ а 2-ні қ осқ анда 8 шығ ады? )
x=6 ө йткені 6+2=8 – тура санды тең дік.
2. 5+x=8 (5-ке қ андай санды қ осқ анда 8 шығ ады? )
x=3, ө йткені 5+3=8 тура санды тең дік
3. x - 2=7 (қ андай саннан 2-ні азайтқ анда 7 шығ ады? )
x=9, ө йткені 9-2=7 - тура санды тең дік.
4. 8 - x=6 (8- ден қ андай санды азайтқ анда 6 шығ ады? )
x=2, ө йткені 8-2=6 – тура санды тең дік
5. х*2=10 (қ андай санды 2-ге кө бейткенде 10 шығ ады? )
x=5, ө йткені 5*2=10- тура санды тең дік.
6. 3*х=6 (3-ті қ андай санғ а кө бейткенде 6 шығ ады? )
x=2, ө йткені 3*2=10- тура санды тең дік
7. х: 2=4 (қ андай санды 2-ге бө лгенде 4 шығ ады? )
x=8, ө йткені 8: 2=4 - тура санды тең дік

8. 6: х=3 ( 6-ны қ андай санғ а бө лгенде 3 шығ ады? )

х=2, ө йткені 6: 2=3 – тура санды тең дік.
Алайда қ ұ рылымы кү рделі жә не деректері кө п таң балы сандармен байланысты болса, сынап кө ру тә сілімен шешу тиімді емес.
Тең деуді шешу тә сілінің келесі тү рінің ә дістемелік негізі амалдардың компоненттері мен нә тижесінің арасындағ ы байланысы болып табылады. Сонда белгісіз компоненттерді табудың ережелері тұ жырымдалады жә не тең деуді шешуде оларғ а сілтеме жасайды.
1. a+x=в, белгісіз екінші қ осылғ ышты табу ү шін, қ осындының мә нін ә ріпті қ осылғ ышты азайту керек, яғ ни х=в-а
2. х+а=в, белгісіз ә ріпті қ осылғ ышты табу ү шін, қ осындының мә нінен екінші қ осылғ ышты азайту керек, яғ ни х=в - а
3. х- а=в, белгісіз азайтқ ышты табу ү шін, айырманың мә ніне азайтқ ышты қ осу керек, яғ ни х=в + а
4. a - x=в, белгісіз азайтқ ышты табу ү шін, азайғ ыштан айырманың мә ні азайту керек, яғ ни х=в - а
5. a*x=в, белгісіз екінші кө бейткішті табу ү шін, кө бейткіштің мә ні бірінші кө бейткішке бө лу керек, яғ ни х=в: а
6. х*а=в, белгісіз бірінші кө бейткішті табу ү шін, кө бейтіндінің мә нін екінші кө бейткішке бө лу керек, яғ ни х=в: а
7. х: а =в, белгісіз бө лінгішті табу ү шін, бө ліндінің мә нін бө лгішке кө бейту керек, яғ ни х=в * а
8. а: х =в, белгісіз бө лгішті табу ү шін, бө лгішті бө ліндінің мә ніне бө лу керек.
Тең деуді шешу тә сілдерін ә дістемелік негізіне тура тең діктің қ асиеттері жә не арифметикалық амалдар қ осу мен азайтудың жә не кө бейту мен бө лудің ө зара кері амалдар екені де алынады.
1. х+а=в Берілген тең деуді екі бө лігіне де бірдей санды қ осқ анда немесе екі бө лгіші де бірдей санды азайтқ анда, берілген тең деуге мә ндес тең деу шығ атынын білеміз. Олай болса, осы тең дікті екі бө ліктен а-ны азайтуғ а болады. Сонда оның сол бө лгішіде х қ алады, яғ ни айнымалы (ә ріп) ал сол бө лгішіде а-в айырма шығ ады, оның мә ні тең деудің тү бірі бө лгіш табылады. Осығ ан ұ қ сас тә сімен а+х=в тең деуін шешуге болады.
2. х- а=в, азайту қ осуғ а кері амал, сондық тан берілген тең деуден, бірден х=в+а жазуғ а кө шеміз. Қ осудың мә ні тең деудің тү бірі болып табылады.
3. a - x=в, азайту қ осуғ а кері амал, сондық тан берілген тең деуден бірден. х+в=а жазуғ а кө шеміз де, ә рі қ арай санғ а тең деудің екі бө лгіштен де в-ны азайтамыз, сонда х=а-в болады. Айырманың мә ні тең деудің тү бірі.
4. х*а=в Берілген тең деуді екі бө лгіш де нө лден ө згеше санғ а бө лгенде немесе кө бейткенде, берілген тең деуге мә ндес тең деу шығ атынын білеміз. Олай болса, осы тең дікті екі бө лгіші де а-ғ а бө луге болады. Сонда оның бө лгіші де х қ алады, яғ ни айнымалы (ә ріп) оқ шауланады, ал сол бө лгішіде в: а бө лінді шығ ады, оның мә ні тең деудің тү бірі болып табылады. Осығ ан ұ қ сас тә сілмен а*х=в тең деуін шешугеболады.
5. х: а =в, бө лу кө бейтуге кері амал, сондық тан берілген тең деуден бірден
х=в * а жазуғ а кө шеміз. Кө бейтіндінің мә ні тең деудің тү бірі болып табылады.
6. а: х =в, бө лу кө бейтуге кері амал, сондық тан берілген тең ждеуден бірден
х*а=в жазуғ а кө шеміз де, ә рі қ арай саң ғ ы тең деудің в-ғ а бө леміз, сонда
х=а: в болады. Бө ліндінің мә ні тең деудің тү бірі.

Сонымен біз жоғ арыда ә дістемелік ә дебиеттерде «Бастауыш мектепте математиканы оқ ыту ә дістемесі» жә не «Бастауыш класстарда математиканы оқ ыту» қ арастырылғ ан тең деу жә не оны шешуге қ атысты ә дістемелік негіздемелерге қ ысқ аша тоқ талдық. Осылардың бірін басшылық қ а алғ ан жағ дайда осы мә селелерді оқ ытып-ү йретудің ө зіндік ә дістемелік жү йесі тү зіледі. Сондық тан да ә р тү рлі автор осылардың бірін таң дап алады да, соғ ан сү йеніп бастауыш сыныптарда тең деу жайында тү сінік қ алыптастырудың жә не тең деулерді шешу тә сілдерін оқ ытып-ү йретудің

ә дістемесіұ сынады.

⇐ Предыдущая 123 4 5 Следующая ⇒