Проверочный тест.. 1 уровень. 2 уровень. 3 уровень

Проверочный тест.

Задания первого уровня проверяют умение решать линейные неравенства при заданных коэффициентах. В заданиях второго уровня один из коэффициентов определяется параметром. В заданиях третьего уровня оба коэффициента зависят от значения параметра. В заданиях четвертого уровня усложняются выражения, содержащие параметры (появляется а²). В заданиях пятого уровня при исследовании значений параметра необходимы знания из других разделов элементарной математики (знание основного тригонометрического тождества, умение раскрывать модуль).

1 уровень

1. Решением неравенства 5x< 7 является:

а) xÎ (-∞; 7/5); б) xÎ (7/5; +∞ );

в) xÎ R; г) xÎ Æ.

2. Решением неравенства 0× x+2< 3 является:

а) xÎ (-∞; 5); б) xÎ (-∞; 9);

в) xÎ R; г) xÎ Æ.

3. Решением неравенства 2x+2³ 2x+7 является:

а) xÎ [5; +∞ ); б) xÎ [5/4; +∞ );

в) xÎ R; г) xÎ Æ.

2 уровень

1. Решением неравенства a x +1> 11 при 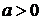является:

а) xÎ (-∞; 10/a); б) xÎ (10/a; +∞ );

в) xÎ R; г) xÎ Æ.

2. Решением неравенства a x -10 < 5 при является

а) xÎ (15; +∞ ); б) xÎ (-∞; 15);

в) xÎ R; г) xÎ Æ.

3. Решением неравенства a x +5³ 18 при является:

а) xÎ [13; +∞ ); б) xÎ [23; +∞ );

в) xÎ R; г) xÎ Æ.

3 уровень

1. При каких значениях параметра a решением неравенства (5+ a)x> a +4 является вся числовая прямая:

а) a =-5; б) a Î (-5; +∞ );

в) ; г) a Î (-∞; -5)?

2. При каких значениях параметра a решением неравенства (3+ a)x£ a -5 является неограниченный промежуток:

а) a =5; б) a =-3;

в) a Î (-∞; -3)È (-3; +∞ ); г) a Î (-∞; 5)È (5; +∞ )?

3. При каких значениях параметра a неравенство (4a +7)x< 3a +2 не имеет решений:

а) a =-7/4; б) a =-2/3;

в) a Î (-7/4; -2/3); г) a Î Æ?

⇐ Предыдущая 123 Следующая ⇒