
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание № 3. Линейные неравенства с параметрами.
Неравенство вида a x> b, a x< b, a x> b, a x< b называется линейным, где x – неизвестная переменная, а a и b – некоторые действительные числа (параметры).
В зависимости от параметров a и b решением линейного неравенства может быть либо неограниченный промежуток, либо вся числовая прямая, либо пустое множество. Всевозможные варианты, возникающие при решении линейных неравенств, отразим в блок-схемах.
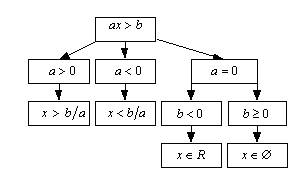
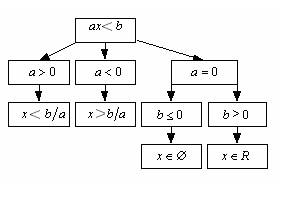
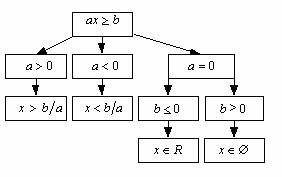
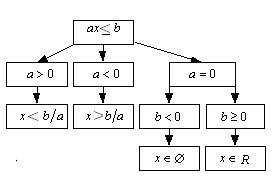
Пример 1. Решить относительно x неравенство 5x – a > ax + 3.
Решение: Преобразуем заданное неравенство:
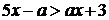
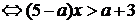
Рассмотрим 3 случая:
1) если 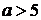 , то решение неравенства –
, то решение неравенства – 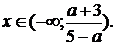
2) если 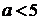 , то
, то 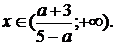
3) если  , то неравенство примет вид 0× x> 8, то есть xÎ Æ.
, то неравенство примет вид 0× x> 8, то есть xÎ Æ.
Ответ: если 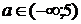 , то
, то 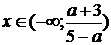 ,
,
если  , то xÎ Æ,
, то xÎ Æ,
если 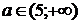 , то
, то 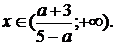
Пример 2. Решить относительно x неравенство 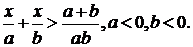
Решение: Преобразуем заданное неравенство:
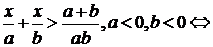
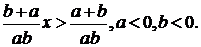
Так как 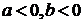 , то
, то 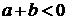 , а
, а  . Следовательно,
. Следовательно, 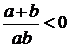 . Учитывая последнее, разделим левую и правую части неравенства на
. Учитывая последнее, разделим левую и правую части неравенства на 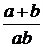 , получая при этом равносильное неравенство x< 1.
, получая при этом равносильное неравенство x< 1.
Ответ: xÎ (-∞; 1) для любых 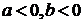 .
.
Пример 3. Решить относительно x неравенство  . (1)
. (1)
Решение: Преобразуем заданное неравенство:
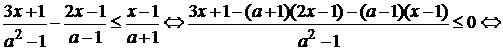
Û 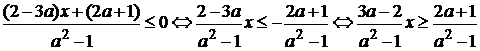 . (2)
. (2)
Рассмотрим 3 случая:
1) 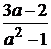 > 0.
> 0.
Решая данное неравенство методом интервалов, находим aÎ (-1; 2/3)È (1; +∞ ). При этих значениях параметра a неравенство (2) равносильно неравенству 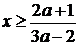 .
.
2) 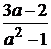 < 0.
< 0.
Решая данное неравенство методом интервалов, находим aÎ (-∞; -1)È (2/3; 1). При этих значениях параметра a неравенство (2) равносильно неравенству 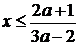 .
.
2) 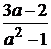 =0, то есть a =2/3. В этом случае неравенство (2) примет вид 0× x³ -21/5, то есть xÎ R.
=0, то есть a =2/3. В этом случае неравенство (2) примет вид 0× x³ -21/5, то есть xÎ R.
Заметим, что при a=±1 исходное неравенство не имеет смысла и решений.
Ответ: если aÎ (-∞; -1)È (2/3; 1), то xÎ (-∞; 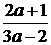 ),
),
если aÎ (-1; 2/3)È (1; +∞ ), то xÎ ( 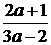 ; +∞ ),
; +∞ ),
если a =2/3, то xÎ R,
если a=±1, то xÎ Æ.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|