2.Показательные уравнения и неравенства.
Пусть a> 0, a¹ 1. Тогда определена показательная функция y=a x, (a x > 0). Основные свойства показательной функции:
ax ay = a x + y
ax / ay = a x - y,
ao = 1, a1 = a.
Решение показательных уравнений проводят по следующей схеме:
-Найти область допустимых значений задачи;
-Привести исходное уравнение к виду a f ( x )= b, либо a f ( x )=a g ( x );
-Выписать соответствующее эквивалентное уравнение f ( x ) = loga b, либо f(x) =g(x);
-Решить полученное уравнение.
Решение показательных неравенств проводят по следующей схеме:
-Найти область допустимых значений задачи;
-Привести неравенство к виду a f ( x ) > b, либо a f ( x ) > a g ( x );
-Выписать соответствующее эквивалентное неравенство:
если a > 1 то f( x ) > loga b, либо f( x ) > g( x );
если 0 < а < 1 то f( x ) < loga b, либо f( x ) < g( x );
-Решить полученное неравенство.
3. Логарифмическая функция
Функцию вида y = loga(x), где a любое положительное число не равное единице, называют логарифмической функцией с основанием а. Здесь и далее для обозначения логарифма мы будем использовать следующую нотацию: loga(b) - данная запись будет обозначать логарифм b по основанию а.
Основные свойства логарифмической функции:
1. Областью определения логарифмической функции будет являться все множество положительных вещественных чисел. Для краткости его еще обозначают R+. Очевидное свойство, так как каждое положительное число имеет логарифм по основанию а.
2. Областью значения логарифмической функции будет являться все множество вещественных чисел.
3. Если основание логарифмической функции a> 1, то на всей области определения функции возрастает. Если для основания логарифмической функции выполняется следующее неравенство 0< a
4. График логарифмической функции всегда проходит через точку (1; 0).
5. Возрастающая логарифмическая функция, будет положительной при x> 1, и отрицательной при 0< х< 1.
6. Убывающая логарифмическая функция, будет отрицательной при х> 1, и положительной при 0< x< 1:
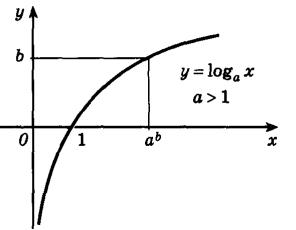 На следующем рисунке представлен график убывающей логарифмической функции - (0< a< 1):
На следующем рисунке представлен график убывающей логарифмической функции - (0< a< 1):
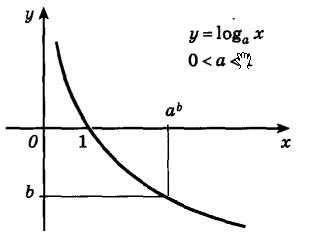 7. Функция не является четной или нечетной. Логарифмическая функция – функция общего вид.
8. Функция не имеет точек максимума и минимума.
7. Функция не является четной или нечетной. Логарифмическая функция – функция общего вид.
8. Функция не имеет точек максимума и минимума.
| 4. Логари́ фм числа  по основанию по основанию 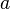 определяется] как показатель степени, в которую надо возвести основание определяется] как показатель степени, в которую надо возвести основание 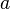 , чтобы получить число , чтобы получить число  . Обозначение: . Обозначение: 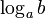 , произносится: " логарифм , произносится: " логарифм  по основанию по основанию 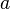 ". Из определения следует, что нахождение ". Из определения следует, что нахождение 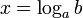 равносильно решению уравнения равносильно решению уравнения 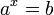 . Например, . Например, 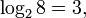 потому что потому что 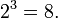 Вычисление логарифма называется логарифмированием. Вычисление логарифма называется логарифмированием.
Основные свойства логарифмов.
При работе с логарифмами применяются следующие их свойства, вытекающие из свойств показательной функции: При любом а> 0 (а≠ 1) и любых положительных х и у выполнены равенства:
1. loga1=0.
2. logaa=1.
3. logaxy =logax + logay.
4. loga  =logax—logay.
5. loga xp=p loga xдля любого действительного р. Для доказательства правила 3 воспользуемся основным логарифмическим тождеством:
x=alogax, y=alogay. (1)
Перемножая почленно эти равенства, получаем:
xy=alogax * alogay= alogax + logay ,
т. е. xy= alogax+ logay . Следовательно, по определению логарифма loga(xy)=logax+ logay. Коротко говорят, что логарифм произведения равен сумме логарифмов. Правило 4 докажем вновь с помощью равенств (1): =logax—logay.
5. loga xp=p loga xдля любого действительного р. Для доказательства правила 3 воспользуемся основным логарифмическим тождеством:
x=alogax, y=alogay. (1)
Перемножая почленно эти равенства, получаем:
xy=alogax * alogay= alogax + logay ,
т. е. xy= alogax+ logay . Следовательно, по определению логарифма loga(xy)=logax+ logay. Коротко говорят, что логарифм произведения равен сумме логарифмов. Правило 4 докажем вновь с помощью равенств (1):
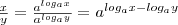 следовательно, по определению
следовательно, по определению 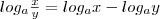 . Говорят, что логарифм частного равен разности логарифмов. Для доказательства правила 5 воспользуемся тождеством x=alogax, откуда хр = (alogax)p= ap logax. Следовательно, по определению logaxP = p loga x. Говорят, что логарифм степени равен произведению показателя степени на логарифм основания этой степени. Основные свойства логарифмов широко применяются в ходе преобразования выражений, содержащих логарифмы. Докажем, например, формулу перехода от одного основания логарифма к другому основанию: . Говорят, что логарифм частного равен разности логарифмов. Для доказательства правила 5 воспользуемся тождеством x=alogax, откуда хр = (alogax)p= ap logax. Следовательно, по определению logaxP = p loga x. Говорят, что логарифм степени равен произведению показателя степени на логарифм основания этой степени. Основные свойства логарифмов широко применяются в ходе преобразования выражений, содержащих логарифмы. Докажем, например, формулу перехода от одного основания логарифма к другому основанию:
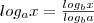 .
(Эта формула верна, если обе ее части имеют смысл, т. е. при x> 0, а> 0 и а≠ 1, b> 0 и b≠ 1. ) По правилу логарифмирования степени и основному логарифмическому тождеству получаем:
logb x = logb( alogax)
откуда
logb x = loga x* logb a
Разделив обе части полученного равенства на logb a, приходим к нужной формуле. С помощью формулы перехода можно найти значение логарифма с произвольным основанием а, имея таблицы логарифмов, составленные для какого-нибудь одного основания b. Наиболее употребительны таблицы десятичных и натуральных логарифмов (десятичными называют логарифмы по основанию 10 и обозначают lg). .
(Эта формула верна, если обе ее части имеют смысл, т. е. при x> 0, а> 0 и а≠ 1, b> 0 и b≠ 1. ) По правилу логарифмирования степени и основному логарифмическому тождеству получаем:
logb x = logb( alogax)
откуда
logb x = loga x* logb a
Разделив обе части полученного равенства на logb a, приходим к нужной формуле. С помощью формулы перехода можно найти значение логарифма с произвольным основанием а, имея таблицы логарифмов, составленные для какого-нибудь одного основания b. Наиболее употребительны таблицы десятичных и натуральных логарифмов (десятичными называют логарифмы по основанию 10 и обозначают lg).
| |
|

 На следующем рисунке представлен график убывающей логарифмической функции - (0< a< 1):
На следующем рисунке представлен график убывающей логарифмической функции - (0< a< 1):
 7. Функция не является четной или нечетной. Логарифмическая функция – функция общего вид.
8. Функция не имеет точек максимума и минимума.
7. Функция не является четной или нечетной. Логарифмическая функция – функция общего вид.
8. Функция не имеет точек максимума и минимума.
 по основанию
по основанию 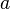 определяется] как показатель степени, в которую надо возвести основание
определяется] как показатель степени, в которую надо возвести основание 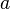 , чтобы получить число
, чтобы получить число  . Обозначение:
. Обозначение: 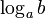 , произносится: " логарифм
, произносится: " логарифм  по основанию
по основанию 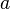 ". Из определения следует, что нахождение
". Из определения следует, что нахождение 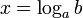 равносильно решению уравнения
равносильно решению уравнения 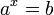 . Например,
. Например, 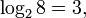 потому что
потому что 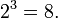 Вычисление логарифма называется логарифмированием.
Вычисление логарифма называется логарифмированием.  =logax—logay.
5. loga xp=p loga xдля любого действительного р. Для доказательства правила 3 воспользуемся основным логарифмическим тождеством:
x=alogax, y=alogay. (1)
Перемножая почленно эти равенства, получаем:
xy=alogax * alogay= alogax + logay ,
т. е. xy= alogax+ logay . Следовательно, по определению логарифма loga(xy)=logax+ logay. Коротко говорят, что логарифм произведения равен сумме логарифмов. Правило 4 докажем вновь с помощью равенств (1):
=logax—logay.
5. loga xp=p loga xдля любого действительного р. Для доказательства правила 3 воспользуемся основным логарифмическим тождеством:
x=alogax, y=alogay. (1)
Перемножая почленно эти равенства, получаем:
xy=alogax * alogay= alogax + logay ,
т. е. xy= alogax+ logay . Следовательно, по определению логарифма loga(xy)=logax+ logay. Коротко говорят, что логарифм произведения равен сумме логарифмов. Правило 4 докажем вновь с помощью равенств (1):
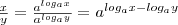 следовательно, по определению
следовательно, по определению 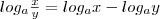 . Говорят, что логарифм частного равен разности логарифмов. Для доказательства правила 5 воспользуемся тождеством x=alogax, откуда хр = (alogax)p= ap logax. Следовательно, по определению logaxP = p loga x. Говорят, что логарифм степени равен произведению показателя степени на логарифм основания этой степени. Основные свойства логарифмов широко применяются в ходе преобразования выражений, содержащих логарифмы. Докажем, например, формулу перехода от одного основания логарифма к другому основанию:
. Говорят, что логарифм частного равен разности логарифмов. Для доказательства правила 5 воспользуемся тождеством x=alogax, откуда хр = (alogax)p= ap logax. Следовательно, по определению logaxP = p loga x. Говорят, что логарифм степени равен произведению показателя степени на логарифм основания этой степени. Основные свойства логарифмов широко применяются в ходе преобразования выражений, содержащих логарифмы. Докажем, например, формулу перехода от одного основания логарифма к другому основанию:
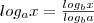 .
(Эта формула верна, если обе ее части имеют смысл, т. е. при x> 0, а> 0 и а≠ 1, b> 0 и b≠ 1. ) По правилу логарифмирования степени и основному логарифмическому тождеству получаем:
logb x = logb( alogax)
откуда
logb x = loga x* logb a
Разделив обе части полученного равенства на logb a, приходим к нужной формуле. С помощью формулы перехода можно найти значение логарифма с произвольным основанием а, имея таблицы логарифмов, составленные для какого-нибудь одного основания b. Наиболее употребительны таблицы десятичных и натуральных логарифмов (десятичными называют логарифмы по основанию 10 и обозначают lg).
.
(Эта формула верна, если обе ее части имеют смысл, т. е. при x> 0, а> 0 и а≠ 1, b> 0 и b≠ 1. ) По правилу логарифмирования степени и основному логарифмическому тождеству получаем:
logb x = logb( alogax)
откуда
logb x = loga x* logb a
Разделив обе части полученного равенства на logb a, приходим к нужной формуле. С помощью формулы перехода можно найти значение логарифма с произвольным основанием а, имея таблицы логарифмов, составленные для какого-нибудь одного основания b. Наиболее употребительны таблицы десятичных и натуральных логарифмов (десятичными называют логарифмы по основанию 10 и обозначают lg).