x=0, y=20=1; Точка А.. x=1, y=21=2; Точка В.. x=2, y=22=4; Точка С.. x=3,y=23=8; Точка D.. x=-1,y=2-1=1/2=0,5; Точка K.. x=-2,y=2-2=1/4=0,25; Точка M.. x=-3, y=2-3=1/8=0,125; Точка N.

Стр 1 из 4Следующая ⇒

· Функцию вида y=a^x, где а> 0, a≠ 1, х – любое число, называют показательной функцией.

· Область определения показательной функции: D (y)= R – множество всех действительных чисел.

· Область значений показательной функции: E (y)= R₊ - множество всех положительных чисел.

· Показательная функция y=a^x возрастает при a> 1.

· Показательная функция y=a^x убывает при 0< a< 1.

Справедливы все свойства степенной функции:

· а⁰=1 Любое число (кроме нуля) в нулевой степени равно единице.

· а¹=а Любое число в первой степени равно самому себе.

· a^x∙ a^y=a^x+y При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.

· a^x: a^y=a^{x- y} При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

· (a^x)^y=a^xy При возведении степени в степень основание оставляют прежним, а показатели перемножают

· (a∙ b)^x=a^x∙ b^y При возведении произведения в степень возводят в эту степень каждый из множителей.

· (a/b)^x=a^x/b^y При возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби.

· а^-х=1/a^x

· (a/b)^-x=(b/a)^x.

Примеры .

1) Построить график функции y=2^x. Найдем значения функции

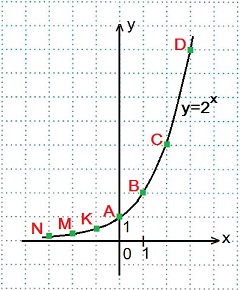при х=0, х=±1, х=±2, х=±3.

x=0, y=20=1; Точка А.

x=1, y=21=2; Точка В.

x=2, y=22=4; Точка С.

x=3, y=23=8; Точка D.

x=-1, y=2-1=1/2=0, 5; Точка K.

x=-2, y=2-2=1/4=0, 25; Точка M.

x=-3, y=2-3=1/8=0, 125; Точка N.

Большему значению аргумента х соответствует и большее значение функции у. Функция y=2^x возрастает на всей области определения D (y)=R, так как основание функции 2> 1.

12 3 4 Следующая ⇒