Пример № 9. Пример № 10. Сочетания.. Определение. Сочетанием без повторений из n элементов по m -называется любое m элементное подмножество n -элементного множества

Пример № 9

Учащиеся 11-го класса изучают 9 учебных предметов. В расписании учебных занятий на один день можно поставить 4 различных предмета. Сколько существует различных способов составления расписания на один день?

Решение.

Имеем 9-элементное множество, элементы которого учебные предметы. При составлении расписания мы будем выбирать 4-элементное подмножество (урока) и устанавливать в нем порядок. Число таких способов равно числу размещений из девяти по четыре, то есть A₉⁴:

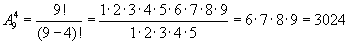
Пример № 10

Сколькими способами из класса, где учатся 24 ученика, можно выбрать старосту и помощника старосты?

Решение.

Имеем 24-элементное множество, элементы которого ученики класса. При выборах старосты и помощника старосты мы будем выбирать 2-элементное подмножество (ученика) и устанавливать в нем порядок. Число таких способов равно числу размещений из девяти по четыре(m=24, n=2), то есть A₂₄²:

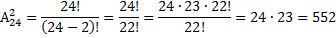
Сочетания.

Сочетаниями из m элементов по n элементов ( n ≤ m ) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных элементов, и которые отличаются друг от друга по крайней мере одним элементом.

Определение. Сочетанием без повторений из n элементов по m -называется любое m элементное подмножество n -элементного множества

Число сочетаний из n элементов по m обозначают 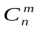(от французского «combination» - «сочетание») и вычисляют по формуле:

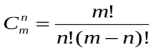
Пример № 11

Сколькими способами из класса, где учатся 24 ученика, можно выбрать два дежурных?

Решение.

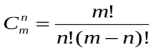
n =24, m=2

⇐ Предыдущая 1 2 3 45