
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Bezobratlí. Obratlovci
Bezobratlí
Perlorodka ř í č ní
Rak kamená č
Č melá k*
Jasoň č ervenooký
Jasoň dymnivkový
Kobylka sá ga
Krajní k*
Kudlanka ná bož ná
Mravenec lesní *
Nosorož ec kapucí nek
Pestrokř í dlec podraž cový
Otaká rek fenyklový
Otaká rek ovocný
Rohá č obecný
Ploskoroh*
Tesař í k alpský
Tesař í k obrovský
Tesař í k zavalitý
Obratlovci
Mihule*
Bě lozubka*
Blatnice skvrnitá
Č olek horský
Č olek karpatský
Č olek veliký
Mlok skvrnitý
Ropucha*
Ješ tě rka*
Slepý š kř ehký
Už ovka hladká
Už ovka podplamatá
Už ovka stromová
Ž elva bahenní
Bě hulí k plavý
Bě loř it š edý
Bramborní č ek*
Brhlí k lesní
Brkoslav severní
Bř ehouš č ernoocasý
Bř ehule ř í č ní
Budní č ek*
Bukač velký
Buká č ek malý
Cvrč ilka*
Č á p bí lý
Č á p č erný
Č eč etka zimní
Č ejka chocholatá
Č ervenka obecná
Č í ž ek lesní
Datel č erný
Datlí k tř í prstý
Dlask tlustozobý
Drop velký
Drozd*
Dř emlí k tundrový
Dudek chocholatý
Dytí k ú horní
Hohol severní
Holub doupň á k
Hví zdá k eurasljský
Hý l obecný
Chř á stal*
Jespá k*
Jež ek*
Jiř ič ka obecná
Kalous pustovka
Kalous uš atý
Ká ně lesní
Koliha*
Kolpí k bí lý
Konipas*
Konopka*
Kopř ivka obecná
Kos horský
Krá lí č ek*
Krutihlav obecný
Kř epelka polní
Kř ivka
Kukač ka obecná
Kulí k*
Kulí š ek nejmenš í
Kvakoš noč ní
Labuť *
Ledň á č ek ř í č ní
Lejsek*
Lelek lesní
Linduš ka*
Luň á k č ervený
Luň á k hně dý
Luně c š edý
Mandelí k hajní
Mlynař í k dlouhoocasý
Morč á k*
Motá k*
Moudivlá č ek luž ní
Myš ivka horská
Netopý r*
Orel*
Orlí k krá tkoprstý
Orlovec ř í č ní
Oř eš ní k kropenatý
Ostralka š tí hlá
Ostř í ž lesní
Ouhorlí k stepní
Pě nice*
Pě nkava jikavec
Pě vuš ka*
Pisí k obecný
Pisila č á ponohá
Plch lesní
Plch zahradní
Poš tolka již ní
Poš tolka obecná
Poš tolka rudonohá
Polá k malý
Potá pka č ernokrká
Potá pka malá
Potá pka rudokrká
Potá pka ž lutorohá
Potá plice*
Puš tí k bě lavý
Puš tí k obecný
Racek*
Rá kosní k*
Raroh velký
Rehek*
Rejsec č erný
Rejsek*
Rorý s*
Rybá k č erný
Rybá k obecný
Sedmihlá sek hajní
Skalní k zpě vný
Skorec vodní
Skř ivan lesní
Skř ivan ouš katý
Slaví k*
Sluč ka malá
Sokol stě hovavý
Sova pá lená
Stehlí k obecný
Strakapoud*
Strnad cvrč í vý
Strnad rá kosní
Strnad zahradní
Stř í zlí k obecný
Sý c rousný
Sý č ek obecný
Sý kora*
Sý koř ice vousatá
Š oupá lek*
Tenkozobec opač ný
Ť uhý k* Turpan*
Vč elojed lesní
Vlaš tovka obecná
Vlha pestrá
Vodouš *
Volavka bí lá
Volavka č ervená
Volavka stř í bř itá
Vrá penec*
Vydra ř í č ní
Vý reč ek malý
Zední č ek skalní
Zrzohlá vka rudozobá
Zvonohlí k zahradní
Ž luna*
Ž luva hajní
OCHRANA Ž IVOTNÍ HO PROSTŘ EDÍ ZVÍ Ř AT
Dnes už ná m nestač í chrá nit jen zví ř ata a rostliny. Moderní společ nost se musí starat i o ochranu jejich ž ivotní ho prostř edí. Zapamatujte si proto ně kolik hlavní ch zá sad kulturní ho č lově ka!
Nikdy nevypalujeme na jař e suchou loň skou trá vu! Nič í me tí m spoustu už iteč né ho hmyzu – př edevš í m sluné č ek a č melá ků – a hubí me pů dní bakté rie, nutné pro rů st vš ech rostlin.
Stará me se o č istotu vodní ch toků, nehá zí me do nich odpadky a bojujeme proti zneč iš ť ová ní ř ek a potoků prů myslový mi odpady.
Chrá ní me, udrž ujeme a upravujeme studá nky a prameny.
Na vhodný ch mí stech vysazujeme remí zky z kř ovin jako vhodná hní zdiš tě pro zpě vné ptactvo.
V lese se chová me tiš e, nezaklá dá me tam oheň a nepohazujeme tam odpadky.
VÝ VOJ ZEMĚ
| Geologická é ra | Geologická perioda | Celkové stá ř í (let) | Vý voj ž ivota |
| Kosmogonické období | 4 500 000 000 až 5 000 000 000 | Vznik Země | |
| Př edgeologické období | Období bezvodé Období praoceá nské | 4 000000 000 až 4 500000 000 | Poč á tek vzniku zemské ků ry |
| Prahory (archaikum) | 2500 000 000 až 4000 000 000 | V oceá nech vzniká ž ivot | |
| Starohory (proterozoikum) | Starš í proterozoikum Mladš í algonkium | 600 000 000 až 2 500 000 000 | Vý voj bezobratlý ch ž ivoč ichů a vý trusný ch rostlin |
| Prvohory (paleozoikum) | Starš í: kambrium ordovik silur devon Mladš í: karbon perm | 225 000 000 až 600 000 000 | Dalš í rozvoj bezobratlý ch, první praryby; rozvoj vý trusný ch cé vnatý ch rostlin; rozš í ř ení kapraď orostů a niž š í ch vý trusný ch rostlin; objevují se první plazi; vyhynuly velké plavuně a př eslič ky; rozvoj nahosemenný ch rostlin |
| Druhohory (mezozoikum) | Trias Jura Kř í da | 1 000 000 až 225 000 000 | Vyhynutí velký ch plazů; poč á tek vý voje krytosemenný ch rostlin; objevují se praptá ci; ohromný rozvoj plazů; objevují se ž á by; poč á tek vý voje savců |
| Tř etihory (tercié r) kenozoikum alpí nské vrá sně ní (poč á tek už v druhohorá ch) | Starš í paleogé n Mladš í neogé n | 1 000 000 až 225 000 000 | Dalš í rozvoj jednodě lož ný ch a dvoudě lož ný ch rostlin; rychlý rozvoj ptá ků a savců; objevují se první lidoopi; podnebí se zač í ná ochlazovat |
| Č tvrtohory (kvarté r) anthropozoikum | Starš í pleistocé n Mladš í holocé n | 0 až 1 000 000 | Doba ledová a meziledová; objevuje se č lově k; rozvoj lidské společ nosti |
GEOLOGICKÉ HODINY
Vyjá dř í me-li stá ř í Země pouhou jednou hodinou, pak jednotlivé geologické doby trvají:
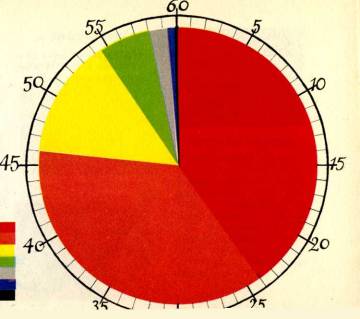

VÝ VOJ Č LOVĚ KA
Př ed 60 000 000 let
Opič í př edek č lově ka ž il na stromech a ž ivil se plody a koř í nky.
Př ed 35 000 000 až 10 000 000 let
Vyhynulí lidoopi (Propliopithecus, Dryopithecus a Kanapithecus) př echá zeli ze stromů na volná prostranství. Chodili polovzpř í meně. Ruka se osvobozovala od chů ze. Vedle potravy rostlinné ž iví se i vejci, malý mi ptá ky a drobný mi savci.
Př ed 2 000 000 až 750 000 let
První lidé (Pithecanthropus a Sinanthropus) už znali oheň, jehož už í vali k ochraně př ed zimou a zvě ř í. Dorozumí vali se posunky a skř eky. Použ í vali ná hodně sebraný ch kamenů, kostí a klacků jako první ch ná strojů. Rozví jela se pracovní č innost. Dovedli primitivně opracová vat ká men. Pě stní klí ny.
Př ed 750 000 až 50 000 let
Neandertá lský č lově k
(Homo sapiens neandertalensis) už vyrá bě l kamenné mlaty a už í val ohně k př í pravě pokrmů. Dorozumí val se ř eč í. Chodil vzpř í meně a bydlel v jeskyní ch, pozdě ji v primitivní ch obydlí ch.
Př ed 50 000 až dneš ek
Č lově k rozumný (Homo sapiens) vytvoř il prvobytnou společ nost. Hovoř il artikulovanou ř eč í. Dochá zí k organizaci lovu (lovci mamutů ). Vyrá bí si stá le dokonalejš í zbraně, ná stroje, ná doby a ozdoby, zprvu z kamene, pozdě ji z bronzu a nakonec ze ž eleza.
STÁ Ř Í Ž IVOČ ICHŮ
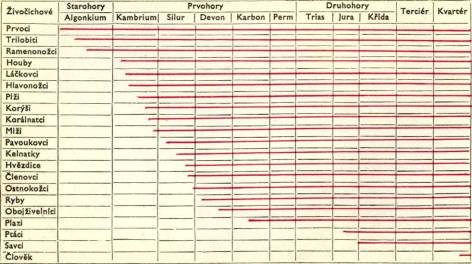
Z vesmí ru a kosmonautiky

ZÁ KLADNÍ Ú DAJE O SLUNCI, MĚ SÍ CI A PLANETÁ CH
| Tě leso | Stř ední vzdá lenost od Slunce (km) | Vzdá l. od Země (v km) Nejmenš í Nejvě tš í | Doba obě hu (dny) | Nejvě tš í prů mě r (v km) | Doba otoč ky kolem osy (dní -min-s) | Zá važ í 1 kg vá ž í na tě lese (kg) | Poč et mě sí ců | ||
| Slunce | – | 147 000 000 | 152 000 000 | 1 391 000 | 28, 4 | – | |||
| Mě sí c | – | 384 400 | 384 400 | 27 dní 8 hod. 43 min. | 3 473 | 27. 8. 1943 | 0, 17 | – | |
| Merkur | 59 910 000 | 79 000 000 | 220 000 000 | 87, 97 dne | 4 840 | ? | 0, 39 | – | |
| Venuš e | 108 210 000 | 40 000 000 | 259 000 000 | 224, 7 dne | 12 400 | ? | 0, 89 | – | |
| Země | 149 600 000 | – | – | 1 rok 0, 26 dne | 12 756 | 23-56-04 | |||
| Mars | 227 900 000 | 57 000 000 | 390 000 000 | 1 rok 321, 98 dne | 6 800 | 24-37-23 | 0, 38 | ||
| Jupiter | 778 300 000 | 590 000 000 | 964 000 000 | 11 roků 317, 6 dne | 142 800 | 9-50-30 | 2, 64 | ||
| Saturn | 1 428 000 000 | 1 200 000 000 | 1 655 000 000 | 29 roků 174 dní | 120 800 | X. 14 | 1, 13 | ||
| Uran | 2 872 000 000 | 2 585 000 000 | 3 150 000 000 | 84 roků 27 dní | 47 600 | X. 49 | |||
| Neptun | 4 498 000 000 | 4 300 000 000 | 4 680 000 000 | 164 roků 324 dní | 44 600 | 15-40 | |||
| Pluto | 5 910 000 000 | 4 275 000 000 | 7 550 000 000 | 248 roků 180 dní | ? | 1 | |||
SEVERNÍ HVĚ ZDNÁ OBLOHA
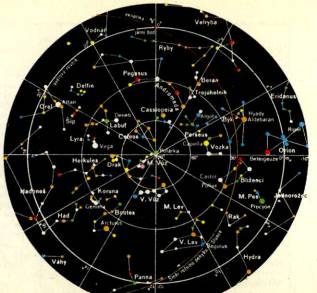
VELKÝ VŮ Z
Vš ichni jistě zná te nejvý razně jš í souhvě zdí naš í oblohy, Velký vů z. Pozná te ho snadno podle jeho sedmi nejjasně jš í ch hvě zd. Má lokdo vš ak ví, ž e celé souhvě zdí tvoř í 133 hvě zd, viditelný ch pouhý m okem! Stař í Arabové dali vš em sedmi hlavní m hvě zdá m jmé na. Postupujeme-li od konce oje k vozu a na jeho obvodu pak ve smě ru hodinový ch ruč ič ek, nachá zí me postupně hvě zdy Benetnaš, Mizar, Alioth, Megrez, Dubhe, Merak a Phekda.
Vš imně te si dobř e druhé hvě zdy v oji! Je to hvě zda Mizar se svou druž icí jmé nem Alkor. Tato hvě zda č tvrté velikosti tvoř í s Mizarem dvojhvě zdu. Stař í Arabové si na Alkoru ově ř ovali zrak. Zkuste to také! Kdo z vá s Alkor tě sně u Mizara v noci vidí, má opravdu dobré oč i.
Mizar s Alkorem je první pouhý m okem objevená dvojhvě zda.
ASTRONOMICKÉ ZNAČ KY
Znač ky pro tě lesa sluneč ní soustavy

Znač ky pro souhvě zdí zvě rokruhu

MĚ Ř ENÍ VZDÁ LENOSTÍ VE VESMÍ RU
Aby astronomové nemuseli poč í tat s obrovský mi č í sly, zavedli si pro mě ř ení vesmí rný ch vzdá leností svě telný rok. Je to vzdá lenost, kterou urazí svě tlo za jeden rok. V kilometrech vyjá dř ený svě telný rok dá vá č í slo 9 462 700 000 000 km, což je devě t bilionů, č tyř i sta dvaaš edesá t miliard, sedm set milió nů kilometrů.
Je-li ně jaká hvě zda vzdá lena od Země 5 svě telný ch roků, znamená to, ž e její svě tlo dorazí na Zemi za pě t let.
Nutnost zavedení svě telné ho roku dosvě dč ují ú daje o ně kte-rý ch vesmí rný ch vzdá lenostech. Tak hvě zda Sí rius je od Země vzdá lena 8, 6 svě t. r., hvě zda Vega 26, 5 svě t. r., mlhovina v Andromedě 680 000 svě t. r. a mlhovina ve Velké m voze 247 760 000 svě t. r.!
Vě tš í astronomickou jednotkou udá vají cí vzdá lenosti je tzv. parsek; rovná se 3, 26 svě telné ho roku.
DŮ LEŽ ITÉ ETAPY DĚ JIN DOBÝ VÁ NÍ VESMÍ RU
| 4. 10. 1957 | První umě lá druž ice SPUTNIK 1 (SSSR) |
| 3. 11. 1957 | Umě lá druž ice SPUTNIK 2 (SSSR) se psem Lajkou |
| 1. 2. 1958 | Umě lá druž ice EXPLORER (USA) |
| 2. 1. 1959 | Mě sí č ní automatická stanice LUNA 1 (SSSR) vyslá na k Mě sí ci |
| 12. 9. 1959 | Mě sí č ní automatická stanice LUNA 2 (SSSR) dopadla na Mě sí c |
| 4. 10. 1959 | Mě sí č ní automatická stanice LUNA 3 (SSSR) vyfotografovala odvrá cenou tvá ř Mě sí ce |
| 19. 8. 1960 | Kosmická loď KOSMICKÁ LOĎ 2 (SSSR) se psy Stř elkou a Bě lkou |
| 12. 2. 1961 | Automatická meziplanetá rní stanice VENĚ RA I (SSSR) vyslá na k Venuš i |
| 12. 4. 1961 | Kosmická loď VOSTOK1 (SSSR); první let po obě ž né drá ze (1x) s č lově kem, J. A. Gagarinem |
| 5. 5. 1961 | Balistická stř ela REDSTONE s kabinou MERCURY (USA); první let do vý š e 188 km a zpě t s kosmonautem A. Shepardem |
| 21. 7. 1961 | Balistická stř ela REDSTONE s kabinou MERCURY (USA); let do vý š e 190 km a zpě t s kosmonautem V. Grissomem |
| 6. -7. 8. 1961 | Kosmická loď VOSTOK 2 (SSSR); let po obě ž né drá ze (17x) s kosmonautem G. S. Titovem |
| 20. 2. 1962 | Kosmická loď FRIENDSHIP 7 (MERCURY 6) (USA); první americký let po obě ž né drá ze s kosmonautem J. Glennem |
| 24. 5. 1962 | Kosmická loď AURORA 7 (USA); let po obě ž né drá ze (3x) s kosmonautem M. S. Carpenterem |
| 11. -15. 8. 1962 | Kosmická loď VOSTOK 3 (SSSR); let po obě ž né drá ze (64x) s kosmonautem A. G. Nikolajevem |
| 12. -15. 8. 1962 | Kosmická loď VOSTOK 4 (SSSR); let po obě ž né drá ze (48x) s kosmonautem P. R. Popovič em |
| 27. 8. 1962 | Kosmická sonda MARINER 2 (USA) vyslá na k Venuš i |
| 3. 10. 1962 | Kosmická loď SIGMA 7 (USA); let po obě ž né drá ze (6x) s kosmonautem W. Shirrou |
| 1. 11. 1962 | Automatická meziplanetá rní stanice MARS 1 (SSSR) vyslá na z tě ž ké druž ice k Marsu |
| 3. 4. 1963 | Mě sí č ní automatická stanice LUNIK 4 (SSSR) vyslá na z umě lé druž ice k Mě sí ci |
| 15. -17. 5. 1963 | Kosmická loď FAITH 7 (USA); let po obě ž né drá ze (22x) s kosmonautem G. Cooperem |
| 14. -19. 6. 1963 | Kosmická loď VOSTOK 5 (SSSR); let po obě ž né drá ze (81x) s kosmonautem V. F. Bykovský m |
| 16. -19. 6. 1963 | Kosmická loď VOSTOK 6 (SSSR); první ž ena ve vesmí ru; let po obě ž né drá ze (48x) s V. V. Tě reš kovovou |
| 1. 11. 1963 | Kosmické tě leso POLJOT 1 (SSSR) za letu mě nilo obě ž nou drá hu |
| 30. 1. 1964 | Kosmický systé m ELEKTRON 1 a ELEKTRON 2 (SSSR); dvě druž ice z jedné rakety vypuš tě ny na rů zné obě ž né drá hy |
| 30. 1. 1964 | Kosmická sonda RANGER 6 (USA) dopadla na Mě sí c |
| 12. 4. 1964 | Kosmické tě leso POLJOT 2 (SSSR) vyzkouš elo mané vrová ní ve vesmí ru |
| 25. 7. 1964 | Mě sí č ní sonda RANGER 7 (USA) vyfotografovala Mě sí c a dopadla na ně j |
| 12. -13. 10. 1964 | Kosmická loď VOSCHOD 1 (SSSR); let po obě ž né drá ze (3x) s tř í č lennou posá dkou: V. Komarov, K. Feoktistov a B. Jegorov |
| 18. -19. 3. 1965 | Kosmická loď VOSCHOD 2 (SSSR); let po obě ž né drá ze (18x), s kosmonauty P. 1. Beljajevem a A. A. Leonovem, který za letu opustil loď |
| 23. 3. 1965 | Kosmická loď GEMINI 3 (USA); let po obě ž né drá ze (3x) se změ nou drá hy; kosmonauti V. Grissom a J. Young |
| 3. 6. 1965 | Kosmická loď GEMINI 4 (USA) s kosmonauty McDivittem a Whitem, který za letu opustil loď |
| 4. 12. -17. 12. 1965 | První setká ní dvou kosmický ch lodí ve vesmí ru: lodi GEMINI 7 (USA) (doba letu 4. -17. 12. 1965) s kosmonauty F. Bormanem aj. Lovellem a GEMINI 6 (USA) (doba letu 15. -16. 12. 1965) s kosmonauty W. Shirrou a G. Staffordem |
| 31. 1. -4. 2. 1966 | Mě sí č ní automatická stanice LUNA 9 (SSSR) mě kce př istá la na Mě sí ci a vyfotografovala jeho povrch |
| 16. 11. 1965-1. 3. 1966 | Automatická stanice VENĚ RA 3 (SSSR) dopadla na Venuš i |
| 31. 3. -3. 4. 1966 | Automatická kosmická stanice LUNA 10 (SSSR) se stala umě lou druž icí Mě sí ce |
| 30. 5. -2. 6. 1966 | Mě sí č ní automatická stanice SURVEYOR 8 (USA) př istá la mě kce na Mě sí ci a fotografovala jeho povrch |
| 3. 6. -6. 6. 1966 | Kosmická loď GEMINI 9 (USA) na obě ž né drá ze s kosmonauty Tomem Staffordem a Eugenem Cernanem, který loď za letu opustil |
| 1. 7. -4. 7. 1966 | Kosmická sonda EXPLORER 33 (USA) vyslá na k Mě sí ci; stala se jeho druhou umě lou druž icí |
| 18. 7. -21. 7. 1966 | Kosmická loď GEMINI 10 (USA) s kosmonauty Johnem Youngem a Mikem Collinsem se na obě ž né drá ze setkala s cí lovou druž icí AGENOU, z ní ž Collins po vystoupení z lodi odmontoval sbě rač mikro-meteoritů |
| 18. 8. -24. 8. 1966 | Umě lá mě sí č ní druž ice LUNAR ORBITER1 (USA) vyslaná k Mě sí ci stala se jeho druž icí |
| 25. 8. 1966 | Automatická stanice LUNA 11 (SSSR) vyslá na k Mě sí ci, kde se stala mě sí č ní druž icí |
| 12. 9. -14. 9. 1966 | Kosmická loď GEMINI 11 (USA) s kosmonauty Charlesem Conradem a Richardem Gordonem navá zala za letu spojení s cí lovou druž icí AGENOU. Gordon za letu opustil loď |
| 17. 4. -20. 4. 1967 | Mě sí č ní sonda SURVEYOR 3 (USA) mě kce př istá la na Mě sí ci s mechanickou lopatou pro zkoumá ní mě sí č ní ho povrchu |
| 12. 6. -18. 10. 1967 | Automatická stanice VENĚ RA 4 (SSSR) př istá la na Venuš i a vyslala zprá vy s fyziká lní mi a chemický mi ú daji |
| 30. 10. 1967 | První automatické spojení sově tský ch kosmický ch lodí na obě ž né drá ze. KOSMOS 188 (vypuš tě n 30. 10. 1967) a KOSMOS 186 (vypuš tě n 27. 10. 1967) |
| 21. 12. -28. 12. 1968 | První oblet Mě sí ce s posá dkou. Kosmická loď APOLLO 8 (USA) s kosmonauty Frankem Bormanem, Jamesem A. Lovellem a Williamem A. Andersem |
| 7. 1. -16. 5. 1969 | Meziplanetá rní stanice VENĚ RA 5 (SSSR) př istá la mě kce na Venuš i a vyslala zprá vy s fyziká lní mi a chemický mi ú daji |
| 17. 8. 1970 | Automatická stanice VENĚ RA 7 (SSSR) vyslá na k Venuš i |
| 18. -24. 9. 1970 | Mě sí č ní automatická stanice LUNA 16 (SSSR) př istá la na Mě sí ci a vrá tila se se vzorky pů dy. První automatický start z kosmické ho tě lesa k Zemi |
| 17. 11. 1970 | Na Mě sí ci př istá la mě sí č ní automatická stanice LUNA 17 (SSSR) a vyslala na mě sí č ní povrch automatický mě sí č ní vozí k LUNOCHOD |
| 31. 1. 1971 | Kosmická loď APOLLO 14 s kosmonauty Allanem Shepardem, Stuartem Roosou a Edgarem Mitchellem; druhé př istá ní lidí na Mě sí ci |
| 25. 4. 1971 | Kosmická loď SOJUZ 10 (SSSR) se spojila s orbitá lní stanicí SALJUT (SSSR) vypuš tě nou 19. 4. 1971 ke společ né mu letu. Kosmonauti Vladimí r Š atalov, Alexej Jelisejev a Nikolaj Rukaviš nikov |
| 8. 6. 1971 | Vytvoř ení první vesmí rné laboratoř e spojení m kosmické lodi SOJUZ 11 (SSSR) s orbitá lní stanicí SALJUT (SSSR). Kosmonauti Georgij Dobrovolskij, Vladislav Volkov a Viktor Pacajev př i ná vratu zahynuli |
| 27. 7. 1971 | Kosmická loď APOLLO 15 (USA) s kosmonauty Alfredem Wordenem, Jamesem Irwinem a Davidem Scottem př istá la na Mě sí ci a po splně ní ú kolů se vrá tila na Zemi |
| 21. 2. 1972 | Na Mě sí ci př istá la automatická stanice LUNA 20 (SSSR) jako první v hornaté č á sti Mě sí ce. 25. 2. 1972 ná vratná č á st stanice př inesla na Zemi vzorky mě sí č ní ch hornin |
| 3. 3. 1972 | Sonda PIONEER 10 (USA) vyslá na k Jupiteru |
| 20. 4. 1972 | Kosmická loď APOLLO 16 (USA) s kosmonauty Johnem W. Youngem, Thomasem K. Mattinglym a Charlesem Moss Dukem př istá la na Mě sí ci a po splně ní ú kolů se vrá tila na Zemi |
| 23. 7. 1972 | První druž ice urč ená k prů zkumu zemské ho prostř edí ERTS (USA) prová dí geologický, geografický i oceá nografický prů zkum a sleduje zamoř ení ovzduš í |
| 7. 12. 1972 | Poslední mě sí č ní vý prava APOLLO 17 (USA) s kosmonauty Eugenem Cernanem, Harrisonem Schmlttem a Ronaldem Evansem př istá la na Mě sí ci. Po splně ní ú kolů se kosmonauti vrá tili na Zemi |
| 3. 4. 1973 | Druhá orbitá lní stanice SALJUT 2 (SSSR) pracovala bez posá dky |
| 6. 4. 1973 | Vyslá na druhá sonda k Jupiteru PIONEER 11 (USA) |
| 19. 4. 1973 | Druž ice INTERKOSMOS 9 (SSSR) vypuš tě na k 500. vý roč í narození Mikulá š e Koperní ka |
| 14. 5. 1973 | Orbitá lní stanice SKYLAB (USA) vypuš tě na na obě ž nou drá hu kolem Země. Postupně se v ní vystř í daly tř i posá dky (na 28 dní, 59 dní a 84 dní ) |
| 21. 7. 1973 | Sonda MARS 4 (SSSR) proletě la kolem Marsu a sní mkovala jeho povrch |
| 25. 7. 1973 | Sonda MARS 5 (SSSR) navedena na obě ž nou drá hu kolem Marsu |
| 5. 8. 1973 | Sonda MARS 6 (SSSR) nesla pouzdro urč ené k př istá ní na Marsu. Př ed dosednutí m vš ak bylo s pouzdrem př eruš eno spojení |
| 9. 8. 1973 | Sonda MARS 7 (SSSR) prolé tla ve vý š i 1300 km nad povrchem Marsu |
| 27. 9. 1973 | Kosmická loď SOJUZ 12 (SSSR) s kosmonauty Vasilijem Lazarevem a Olegem Makarovem provedla dvoudenní experimentá lní let |
| 30. 10. 1973 | Druž ice INTERKOSMOS 10 jako společ ná druž ice socialistický ch zemí prová dě la vý zkum kosmické ho prostoru. Př í stroje pro ni dodali naš i odborní ci |
| 3. 11. 1973 | Sonda MARINER 10 (USA) vyslá na na prů zkum planet Venuš e a Merkuru |
| 18. 12. 1973 | Kosmická loď SOJUZ 13 (SSSR) s kosmonauty Petrem Klimukem a Valentinem Lebedě vem prově ř ila př i osmidenní m letu zlepš enou verzi lodi SOJUZ a plnila vě decký vý zkum |
| 25. 6. 1974 | Orbitá lní stanice SALJUT 3 (SSSR) př ijala z paluby kosmické lodi SOJUZ 14 kosmonauty Pavla Popovič e a Jurije Arť uchina |
| 2. 12. 1974 | Start kosmické lodi SOJUZ 16 (SSSR) s kosmonauty A. G. Filipč enkem a N. N. Rukaviš nikovem. Generá lní zkouš ka pro chystaný společ ný let Sojuz/Apollo |
| 8. 6. 1975 | Meziplanetá rní sonda VENĚ RA 9 (SSSR) odstartovala za dalš í mi vý zkumy Venuš e. U cí lové planety se rozdě lila na orbitá lní č á st, která byla navedena na obě ž nou drá hu kolem Venuš e, a na vý sadkový modul, který mě kce dosedl na povrchu planety. Poprvé byly zí ská ny sní mky Venuš e z bezprostř ední blí zkosti |
| 16. 6. 1975 | Meziplanetá rní sonda VENĚ RA 10 (SSSR) odstartovala se stejný m programem letu jako sonda VENĚ RA 9 a své ú koly splnila |
| 15. 7. 1975 | Kosmická loď SOJUZ 19 (SSSR) s kosmonauty A. A. Leonovem a V. N. Kubaš svem odstartovala k první mu sově tsko-americké mu kosmické mu letu, aby se na obě ž né drá ze spojila s kosmickou lodí Apollo |
| 15. 7. 1975 | Kosmická loď APOLLO (USA) s kosmonauty T. P. Staffordem, V. D. Brandem a D. K. Slaytonem odstartovala ke společ né mu letu se SOJUZEM 19 |
| 20. 8. 1975 | Meziplanetá rní sonda VIKING 1 (USA) odstartovala k Marsu. Po př istá ní vý sadkové ho modulu sondy na povrchu planety provedla sonda vě decká mě ř ení, analý zu vzorků hornin, sní mkovala nejbliž š í okolí a pá trala po mimozemské m ž ivotě |
| 9. 9. 1975 | Meziplanetá rní sonda VIKING 2 (USA) odstartovala se stejný m programem letu jako př edchozí sonda a své ú koly splnila |
| 17. 11. 1975 | Kosmická loď SOJUZ 20 (SSSR) bez posá dky se automaticky spojila s orbitá lní stanicí SALJUT 4 a lé tala kolem Země celkem 51 dnů. Š lo o zkouš ku mož nosti zá sobová ní orbitá lní ch stanic nepilotovaný mi zá sobovací mi lodě mi |
| 26. 11. 1975 | Druž ice CHINA 4 (Č LR) odstartovala na obě ž nou drá hu kolem Země a její č á st po š estidennlm letu př istá la zpá tky na Zemi |
| 11. 9. 1976 | Kosmická loď SOJUZ 22 (SSSR) s kosmonauty V. Bykovský m a V. Aksjonovem odstartovala na obě ž nou drá hu kolem Země. Př i samostatné m letu byly uskuteč ně ny experimenty programu Interkosmos s fotografickou aparaturou z NDR |
Z mineralogie
SOUSTAVA NEROSTŮ
Nerosty jsou prvky nebo chemické slouč eniny, které tvoř í zemskou ků ru. Dě lí me je do deseti skupin.
1. Prvky: Uhlí k (diamant, tuha), sí ra, mě ď, zlato apod.
2. Sirní ky: Pyrit (kyz ž elezný ), chalkopyrit (kyz mě dě ný ), galenit (leš tě nec olově ný ), sfalerit apod.
3. Halovce: Sů l kamenná (chlorid sodný ), kazivec (fluorid vá penatý ) apod.
4. Kyslič ní ky (oxidy): Voda, kř emen (kyslič ní k kř emič itý ), krevel (kyslič ní k ž elezitý ), hně del (vodnatý kyslič. ž elezitý ), cí novec (kyslič ní k cí nič itý ) atd.
5. Uhlič itany: Vá penec (uhlič itan vá penatý ), magnezit (uhlič itan hoř eč natý ), ocelek (uhlič itan ž eleznatý ) atd.
6. Kř emič itany: Slouč eniny kř emí ku, kyslí ku a rů zný ch prvků (ž ivce, slí dy, kaolinit, graná t, smaragd atd. ).
7. Dusič nany: Ledek sodný (chilský ) atd.
8. Fosforeč nany: Apatit (fosforeč nan vá penatý ) atd.
9. Sí rany: Sá drovec (vodnatý sí ran vá penatý ) atd.
10. Nerosty organické: Jantar, uhlí, asfalt, zemní vosk, ropa atd.
Poč et druhů dosud zná mý ch nerostů je asi 2000.
PŘ EHLED NĚ KTERÝ CH NEROSTŮ
| Jmé no | Chemický ná zev | Chemický vzorec |
| Ametyst | kyslič ní k kř emič itý | SiO2 |
| Amfibol | kř emič itan prvků Mg, Ca, Fe, Na, Al, Ti aj. | |
| Antimonit | sirní k antimonitý | Sb2S3 |
| Aragonit | uhlič itan vá penatý | CaCO3 |
| Argentit | sirní k stř í brný | Ag2S |
| Arzenopyrit | sirní k arzé nu a ž eleza | FeAsS |
| Auripigment | sirní k arzenitý | As2S3 |
| Azbest (osinek) | kř emič itan vá penatohoř eč natý | |
| Baryt | sí ran barnatý | BaSO4 |
| Bauxit | hydroxid hlinitý | Al(OH)8 |
| Burel (pyroluzit) | kyslič ní k manganič itý | MnO2 |
| Cí novec (kasiterit) | kyslič ní k cí nič itý | SnO2 |
| Dolomit | uhlič itan hoř eč natová penatý | CaCO3. MgCO3 |
| Galenit | sirní k olovnatý | PbS |
| Graná t č eský | ortokř emič itan hlinitohoř eč natý | Mg3Al2(SiO4)3 |
| Hadec (serpentin) | kř emič itan hoř eč natož eleznatý | H4(MgFe)2SiO9 |
| Hně del (limonit) | hydroxid ž elezitý | Fe(OH)3 |
| Hoř ká sů l (epsomit) | sí ran hoř eč natý | MgSO4 |
| Chalcedon | kyslič ní k kř emič itý | SiO2 |
| Chalkopyrit | sí rož elezitan mě dný | CuFeS2 |
| Kalomel | chlorid rtuť ný | Hg2Cl2 |
| Kazivec (fluorit) | fluorid vá penatý | CaF2 |
| Korund | kyslič ní k hlinitý | Al2O3 |
| Krevel (hematit) | kyslič ní k ž elezitý | Fe2O3 |
| Kř emen | kyslič ní k kř emič itý | SiO2 |
| Kuprit | kyslič ní k mě dný | Cu2O |
| Magnezit | uhlič itan hoř eč natý | MgCO3 |
| Malachit | zá saditý uhlič itan mě ď natý | CuCO3. Cu(OH)2 |
| Markazit | dvojsirní k ž eleza | FeS2 |
| Mastek | kyselý metakř emič ltan hoř eč natý | H2Mg3(SiO3)4 |
| Molybdenit | sirní k molybdenu | MoS3 |
| Nikelin | arzenid nikelnatý | NiAs |
| Ortoklas (ž ivec) | kř emič itan hlinitodraselný | KAlSi3O8 |
| Pyrargyrit | sirní k antimopitostř í brný | 3Ag2S. Sb2S3 |
| Pyrit | dvojsirní k ž eleza | FeS2 |
| Rumě lka (cinabarit) | sirní k rtuť natý | HgS |
| Sfalerit | sirní k zlneč natý | ZnS |
| Sů l kamenná (kuchyň ská ) | chlorid sodný | NaCl |
| Sylví n | chlorid draselný | KCl |
| Vá penec (kalcit) | uhlič itan vá penatý | CaCO3 |
| Zá hně da | kyslič ní k kř emič itý | SiO2 |
STUPNICE TVRDOSTI
1 Mastek
2 Sů l kamenná
3 Vá penec (Kalcit)
4 Kazivec (fluorit)
5 Apatit
6 Ž ivec (Ortoklas)
7 Kř emen
8 Topaz
9 Korund
10 Diamant
Z matematiky
Nejbě ž ně jš í znaky a spojky v matematický ch zá pisech:

MNOŽ INY
Množ ina je ně jaký souhrn, např. matematický ch objektů (č í sel, bodů, př í mek apod. ) nebo osob, vě cí apod. sice libovolný ch, ale s takovou urč enou vlastností, ž e je mož no o kaž dé m uvaž ované m objektu jednoznač ně prohlá sit, zda do množ iny patř í, nebo nepatř í.

Zná zorně no na diagramech:
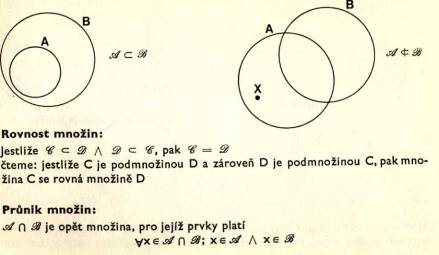
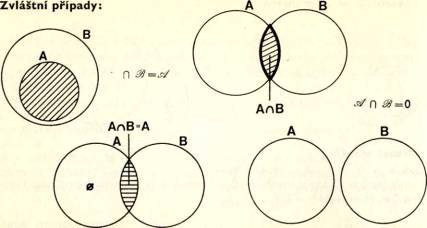
Množ iny nemají cí ž á dný společ ný prvek (jejich prů nik je prá zdná množ ina) nazý vají se disjunktní. Např. množ ina lichý ch č í sel a množ ina sudý ch č í sel jsou disjunktní; ž á dné č í slo není zá roveň liché i sudé. Ale: polopř í mka AB jako množ ina bodů a polopř í mka k ní opač ná mají jediný společ ný bod (totiž bod A). Tyto množ iny nejsou disjunktní (jejich prů nik je jednoprvková množ ina bod A).
n množ ina č í sel př irozený ch (1, 2, 3, 4, 5…)
Z množ ina č í sel celý ch (…, -3, -2, -1, 0, 1, 2, 3, …)
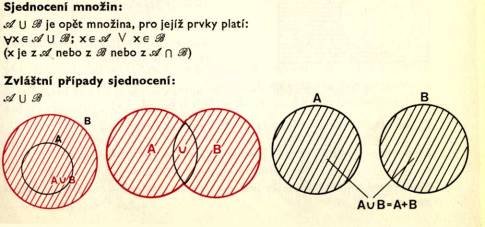
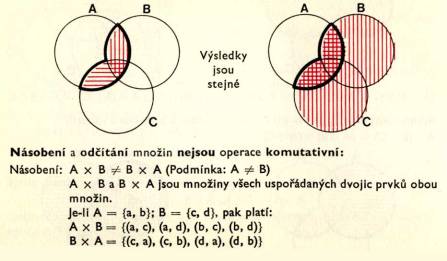
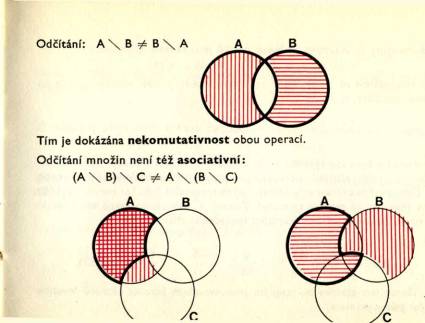
Q, množ ina č í sel racioná lní ch (např. 3, -2/3, 0, 6, 2, -4, 7, …) Sjednocení a prů nik množ in jsou operace komutativní:
Sjednocení a prů nik množ in jsou operace asociativní – nezá lež í na poř adí operace:
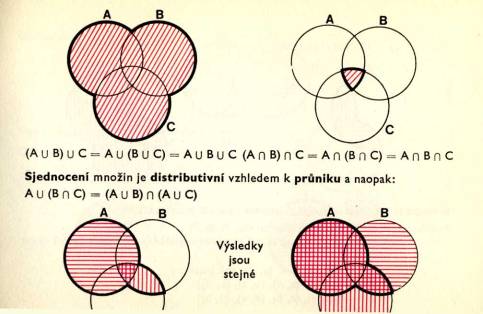
a n (b u C)= (a n b) u (a n c)
Koneč né množ iny se stejný m poč tem prvků jsou stejně mohutné:
n (A) = 4; n (B) = 4; N (A) = n (B) Množ iny rozlož í me na tř í dy, když umí stí me kaž dý prvek množ iny prá vě do jedné podmnož iny, tj. tř í dy.
ZLOMKY
Kaž dé racioná lní č í slo lze vyjá dř it v dekadické m pozič ní m systé mu buď ukonč ený m zá pisem, nebo zá pisem periodický m (opakují cí se poslední č í slice nebo skupinu č í slic znač í me č á rou nad č í slicí ). Kaž dé racioná lní č í slo lze rovně ž vyjá dř it zlomkem (nekoneč ně mnoha způ soby). Zlomek v zá kladní m tvaru má č itatele i jmenovatele č í sla nesoudě lná (nemají cí společ né ho dě litele). Př í klad:
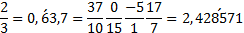
Sč í tat mů ž eme jen zlomky se stejný m jmenovatelem (souč et č itatelů lomí me společ ný m jmenovatelem).
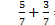
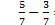
Nemají -li zlomky stejné ho jmenovatele, rozš í ř ení m je na stejné ho jmenovatele uvedeme.
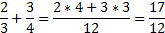
Zlomek ná sobí me zlomkem tak, ž e souč in č itatelů lomí me souč inem jmenovatelů.
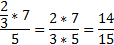
Zlomek dě lí m zlomkem rů zný m od nuly tak, ž e dě lence ná sobí me př evrá cený m dě litelem
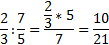
Slož ený zlomek je jiný zá pis dě lení zlomků
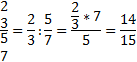
Dě litel (jmenovatel zlomku) se nikdy nesmí rovnat nule! (Př i dě lení nulou bychom totiž v ž á dné m př í padě souč inem dě litele a podí lu, což je zkouš ka sprá vnosti dě lení, nedostali nenulové ho dě lence. )
Ú MĚ RA
a: b = c: d pro a, b, c, d ≠ 0 Souč in vně jš í ch č lenů se rovná souč inu č lenů vnitř ní ch: ad = bc
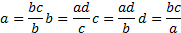
PROCENTA
z zá klad (100%)
a č á st
p poč et procent %
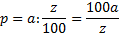
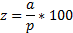
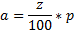
JEDNODUCHÉ Ú ROKOVÁ NÍ
j jistina (100 %)
u ú rok
p poč et %
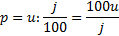
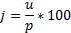
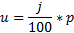
PŘ EHLED Č Í SELNÝ CH Ř Á DŮ

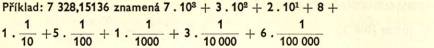
Ř í ká me, ž e sedmič ka je ř á du tř etí ho (tisí ců ), trojka ř á du druhé ho (stovek), dvojka ř á du první ho (desí tek), osmič ka ř á du nulté ho (jednotek), jednič ka ř á du minus první ho (desetin), pě tka ř á du minus druhé ho (setin) atd.
Desí tková soustava je pro bě ž né poč í tá ní nejvhodně jš í. Dř í ve se použ í valo např. soustavy pě tkové (podle pě ti prstů na ruce), dvací tkové (francouzsky 80 je quatrevingt, což je 4. 20) nebo š edesá tkové. Elektrické poč í tač e už í vají soustavy dvojkové.
REÁ LNÁ Č Í SLA
Zaokrouhlová ní reá lný ch č í sel:
Cifry 0, 1, 2, 3, 4 zaokrouhlujeme dolů (vynechá me je).
Cifry 5, 6, 7, 8, 9 zaokrouhlujeme nahoru (př edchozí cifru o jednotku zvě tš ujeme), např.: 7 328, 15 zaokrouhleno na desetiny 7 328, 2
zaokrouhleno na stovky 7 300
zaokrouhleno na tř i platné č í slice 7 330
0, 0397 zaokrouhleno na setiny 0, 04
zaokrouhleno na dvě platné č í slice 0, 040
3, 82 zaokrouhleno na setiny 3, 83
Absolutní hodnota reá lné ho č í sla
kladné ho je toté ž č í slo kladné a > 0 |a| = a |3| = 3
zá porné ho je č í slo opač né a < 0 |a| = –a |-6| = – (-6) = +6
nuly je nula a = 0 |a| = 0 |9-32| = 0
Sluč ová ní reá lný ch č í sel:
Odeč í st č í slo znamená př ič í st opač né. Souč et dvou kladný ch č í sel je č í slo kladné (absol. hodnoty sč í tá me). Souč et dvou zá porný ch č í sel je č í slo zá porné (absol. hodnoty sč í tá me).
Ná sobení reá lný ch č í sel:
Souč in dvou kladný ch č í sel je č í slo kladné.
Souč in dvou zá porný č í sel je č í slo kladné. Souč et č í sla kladné ho a zá porné ho má znamé nko č í sla s vě tš í absol. hodnotou a absol. hodnoty odč í tá me.
Souč in č í sla kladné ho a zá porné ho je č í slo zá porné. Stejná znamé nka platí i pro dě lení dě litelem rů zný m od nuly.
POŘ ADÍ POČ ETNÍ CH VÝ KONŮ
1. vý kony v zá vorká ch
2. umocň ová ní a odmocň ová ní
3. ná sobení, dě lení
4. sluč ová ní
Př í klad: (2-3)2. 5-3. 42 = (-1)2. 5 - 3. 16 = -43
Pozor: (-3) 2 = + 9, ale –32 = –9
NÁ SOBENÍ A ROZKLAD MNOHOČ LENŮ
Mnohoč len ná sobí me mnohoč lenem tak, ž e kaž dý č len první ho mnohoč lenu
ná sobí me kaž dý m č lenem druhé ho a jednotlivé souč iny slouč í me.
(a + b – c). (d – e) = ad – ae + bd – be – cd + ce
Rozlož it mnohoč len (č í slo) znamená vyjá dř it jej jako souč in jednoduchý ch mnohoč lenů (prvoč í sel). Rozklad prová dí me nejč astě ji vytý ká ní m př ed zá vorku a podle vzorců (viz dá le! ).
MOCNINY A ODMOCNINY


Bez zá pisu zpamě ti:
472 (zač í ná me odzadu podle vzorce (a + b) 2:
72 je 49; devě t napí š eme, č tyř i př ipoč teme……………………… 9
2. 4. 7 je 56 a 4 je 60; nulu napí š eme, 6 př ipoč teme………………… 09
42 je 16 a 6 je 22…………………………………………… 2209

c) zpamě ti urč í me dvojmoc dvojciferné ho č í sla zakonč ené ho pě tkou, když k první mu č í slu př ipoč teme jednu a ná sobí me první m č í slem. K vý sledku př ipí š eme 25.
Např. 252…… (2 + 1). 2……… 6 a př ipí š eme 25……… 625
452…… (4 + 1). 4……… a př ipsat 25…………… 2025
652…… (6 + 1). 6……… a př ipsat 25…………… 4225
Druhé a tř etí mocniny, které stojí za zapamatová ní:
112 = 121
122 = 144
132 = 169
142 = 196
152 = 225
162 = 256
172 = 289
182 = 324
192 = 361
202 = 400
13= 1
23= 8
33= 27
43 = 64
53 = 125
63 = 216
73 = 343
83 = 512
93 = 729
103 = 1000
Vzorce k zapamatová ní:
(a ± b) 2 = a2 ± 2ab + b2
(a ± b) 3 = a3 ± 3a2b + 3ab2 ± b8
a2 – b2 = (a + b). (a – b)
a3 + b3 = (a + b). (a2 – ab + b2)
a3 – b3 = (a – b). (a2 + ab + b2)
Pozor! a2 + b2 se nedá v R rozlož it!
Odstraň ová ní odmocniny ze jmenovatele v nejjednoduš š í ch př í padech:
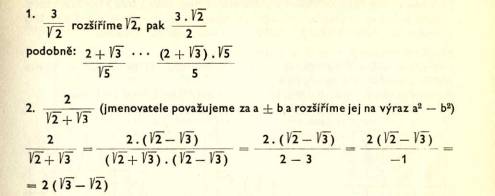
Př í pustné ú pravy rovnice:
1. Lze př ič í st k obě ma straná m rovnice toté ž č í slo.
2. Lze ná sobit obě strany rovnice tý mž č í slem rů zný m od nuly.
FUNKCE
Př iř azujeme-li k reá lný m č í slů m x jednoznač ně opě t reá lná č í sla y (ke kaž dé mu x nejvý š e jwdno y), hovoř í me o funkč ní zá vislosti. Množ ina x je takzvaná množ ina promě nný ch (definič ní obor), množ ina y je obor funkč ní ch hodnot.
Lineá rní funkce y = kx + q; grafem je př í mka.
x je promě nná, y je funkč ní hodnota, k je smě rnice (tangens ú hlu sevř ené ho grafem s osou x), q je ú sek na ose y.
Zvlá š tní př í pady: q = 0 Př í mka prochá zí poč á tkem (př í má ú mě rnost).
k = 0 Funkce konstantní (graf je rovnobě ž ka s osou x).
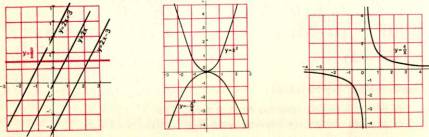
Kvadratická funkce y = kx2. Graf je parabola s vrcholem v poč á tku.
Nepř í má ú mě rnost y = k/x ≠ 0. Graf je rovnoosá hyperbola, x
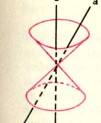
Parabola a hyperbola spolu s elipsou a kruž nicí patř í do množ iny kuž eloseč ek, tj. rovinný ch prů seků obliny rotač ní ho kuž ele. Ta vznikne otá č ení m jedné rů znobě ž ky (a) kolem druhé (b), která je osou nekoneč ně vysoké ho dvojkuž ele (viz obr. 1), jehož vrchol je prů seč í k rů znobě ž ek. Seč ná rovina nesmí prochá zet vrcholem. Je-li ú hel rů znobě ž ek < p a ú hel roviny s osou a, mohou nastat 4 př í pady:
1. 0 < = α < φ hyperbola (2 vě tve) (h1, h2)
2. α = φ parabola (p)
3. φ < α < R elipsa viz obr. 2 (e)
4. α = R kruž nice (k)
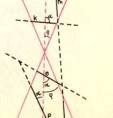
Kdyby rovina prochá zela vrcholem dvojkuž ele, pak by nastaly tyto př í pady:
a) α = 0 dvě mimobě ž ky sví rají cí ú hel ß = 2φ
b) 0 < α < φ dvě mimobě ž ky sví rají cí ú hel 0 < ß < 2φ
c) α = φ jedna př í mka povrchová
d) φ < α < =R bod – vrchol dvojkuž elí
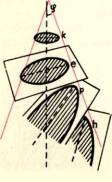
Kdyby vrchol kuž ele byl zdroj svě tla, které mu bychom dali do cesty neprů hledný kruh, vytvoř í paprsky oblinu (plá š ť ) kuž ele a kruh vrhá na nakloně né roviny stí ny elipsy, paraboly nebo hyperboly, podle ú hlu sklonu (viz obr. 3). Stejný jev lze pozorovat, vrhneme-li na stě nu svě telný kuž el lampy. Té ž nakloně ní m uzavř ené kuž elovité skleně né ná dobky (Erlenmayerovy baň ky) naplně né kapalinou dostaneme kuž eloseč ky jako prů seky její hladiny se stě nou baň ky.
Př í sluš né rovnice kuž eloseč ek:
Kruž nice (stř edová ) x2 + y2 = r2
Elipsa (stř edová ) b2x2+ a2y2 = a2b2 (kde a a b jsou osy kř ivek)
Hyperbola (osová ) b2x2 – a2y2 = a2b2
Parabola (vrcholová ) y = 2px
Funkce ostré ho ú hlu v pravoú hlé m trojú helní ku:

Hodnoty funkcí ně který ch ú hlů si snadno zapamatujeme podle obrá zků:
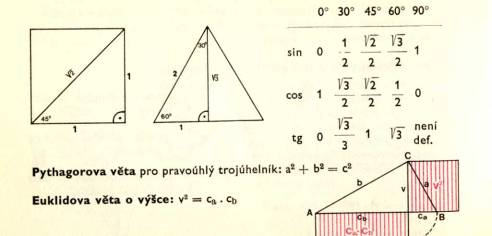
Euklidova vě ta o odvě sně:
b2 = c. cb a2 = c. ca
a2 + b2 = c. ca + c. cb = c (ca + cb) = c2
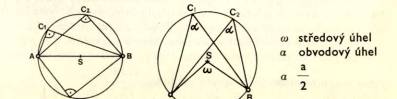
Thaletova vě ta:
Geometrický m mí stem vrcholů pravoú hlý ch trojú helní ků o př eponě AB je kruž nice o prů mě ru AB bez bodu A, B.
(Struč ně: vš echny ú hly nad prů mě rem jsou pravé. ) Jde o zvlá š tní př í pad obvodový ch ú hlů: Obvodový ú hel se rovná polovině ú hlu stř edové ho.
Vně jš í ú hel trojú helní ka se rovná souč tu vnitř ní ch ú hlů u ostatní ch vrcholů. U té hož vrcholu jsou dva shodné vně jš í ú hly (vrcholové ) γ ‘
γ + γ ‘ = 180° ú hly vedlejš í

Tě ž nice trojú helní ka spojují vrchol se stř edem protě jš í strany. Prů seč í k tě ž nice – tě ž iš tě – lež í v jedné tř etině dé lky tě ž nice (od strany). Prů seč í k os stran je stř edem kruž nice trojú helní ku opsané. Prů seč í k os ú hlů je stř edem kruž nice trojú helní ku vepsané. Stř ední př í č ka trojú helní ka spojuje stř edy dvou stran. Je rovnobě ž ná se stranou, kterou neprotí ná, a je její polovinou. V rovnostranné m trojú helní ku tě ž nice, vý š ky, osy stran a osy ú hlů splý vají.
Vý š ka rovnostranné ho trojú helní ka má dé lku- (a * odmocnina 3) / 2
OBSAHY A OBVODY ROVINNÝ CH Ú TVARŮ

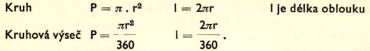
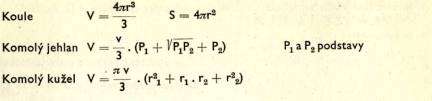
OBJEMY A POVRCHY TĚ LES

VEKTOR
1, je množ ina vš ech ekvipolentní ch dvojic s danou dvojicí (uspoř á daná dvojice AB je ekvipolentní s uspoř á danou dvojicí CD, jestliž e ú seč ky AD a BC mají společ ný stř ed).
B
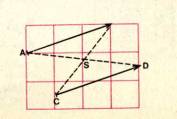

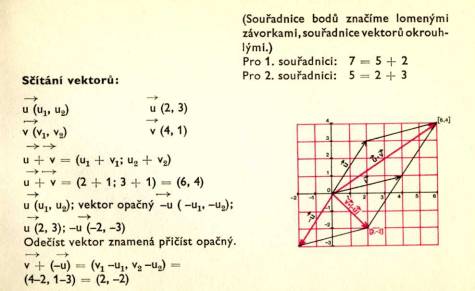
Z FYZIKY
Fyzika je př í rodní vě da, která zkoumá vlastnosti a pohyby hmoty.
ROZDĚ LENÍ FYZIKY

Nejdů lež itě jš i velič iny, které ve fyzice mě ř í me, jsou: dé lka, hmotnost (zjiš ť ujeme ji nejč astě ji vá ž ení m) a č as (viz Mí ry a vá hy).
Znač ky fyziká lní ch velič in:
Dé lka (l), drá ha (s), plocha (S), objem (V), ú hel (φ ), č as (t), doba kmitu-perloda (T), kmitoč et (f), vlnová dé lka (lambda), rychlost (v), zrychlení (a), hmotnost (m), hustota (ρ ), sí la (F), tí ha-vá ha (G), mě rná tí ha (γ ), tlak (p), prá ce (A), energie (W), vý kon (P), teplo (Q), napě tí (U), proud (I), elektrický ná boj (Q), odpor (R), mě rný odpor (ρ ), kapacita (C)
MECHANIKA TĚ LES
Hmotnost a hustota
Hmotnost (m) dvou tě les je stejná, mají -li také stejnou tí hu (vá hu G). Hmotnosti rů zný ch tě les se zjiš ť ují vá ž ení m. Hmotnosti tě les z té ž e lá tky jsou tolikrá t vě tš í, kolikrá t vě tš í je jejich objem. Jednotkou hmotnosti je 1 kg (kilogram). Hustota (ρ )tě lesa je hmotnost tě lesa o jednotkové m objemu:
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|