
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Сумма коэффициентов, кроме первого и второго, сокращённых на P
Усовершенствование методов: поиска и алгоритмов генерации простых чисел
Даная работа рассматривает проблематику не совершенство методов: поиска и алгоритмов генерации простых чисел. А именно: поиск простых чисел, на данный момент времени, осуществляется либо путём оценки и исследовании малой теоремы Ферма (МТФ), обобщенной до теорем: Кармайкла и Лангража для конечных циклических групп. Либо путём оценки и исследовании теста Агравала-Каяла-Саксены (AKS-тест). Что влечёт за собой: в первом случае полиномиальность вычислений, т. е. сложность вычисления растёт в зависимости от входных данных, но количество которых находится в разумных пределах. Во втором же случае, полиномиальность т. е. сложность вычисления, слабо зависима от входных данных, однако количество которых растёт, в зависимости от величины проверяемого числа. Что автоматически усложняет алгоритмы генерации простых чисел.
Также в данной работе, рассматриваются методы, значительно понижающие сложность вычисления, при максимально сокращении, алгоритмов: вычисления и генерации простого числа.
Решение данной проблематики, начинается с оценки уже существующих методах, что описаны выше, а также обоснования их применения.
А именно: проведена работа по сопоставлению оного метода другому.
В результате которой была обнаружено закономерность, значительно упрощающая затраты на вычисления, при повышении достоверности результата. А также, выявлен метод, повышающий степень надёжности вычисления, при генерации простых чисел.
Для усовершенствования методов: поиска и алгоритмов генерации простых чисел нам потребуются: AKS (истинный тест простоты), бином Ньютона и МТФ.
Сперва рассмотрим и осознаем, как работает и что на может дать, тест Агравала-Каяла-Саксены (AKS-тест)
Тест Аграва́ ла — Кая́ ла — Саксе́ ны ( тест AKS ) — единственный известный на данный момент универсальный (то есть применимый ко всем числам) полиномиальный, детерминированный и безусловный (то есть не зависящий от недоказанных гипотез) тест простоты чисел, основанный на обобщении малой теоремы Ферма на многочлены.
Формулировка Теста Аграва́ ла — Кая́ ла — Саксе́ ны
Здесь и далее or(n) обозначает показатель числа n по модулю r, log — двоичный логарифм и φ (⋅ ) — функция Эйлера.
Сравнение по двум модулям вида a(x)≡ b(x)(modh(x), n) для многочленов a(x), b(x)∈ \Z[x] означает, что существует g(x)∈ \Z[x] такой, что все коэффициенты многочлена a(x)− b(x)− g(x)h(x) кратны n, где \Z[x] — кольцо многочленов от x над целыми числами.
Т. е. Возведённый многочлен вида (x-1) в степень P. Даст все коэффициенты, за исключением стоящих при наивысших степенях равных P, делящиеся без остатка на P.
Для удобства работы с AKS-тестом, используем Бином Ньютона.
Пере формулировка теста простоты (истинного), при помощи
формулы бинома Ньютона
Бином Ньютона
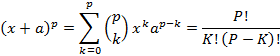
Поскольку биномиальные коэффициенты дублируются, имеет смысл рассматривать лишь уникальные их значения. Исходя из этого, определим их количество.
(P-1)/2 – Количество уникальных биномиальных коэффициентов.
Исходя из того, что, каждый биномиальный коэффициент, за исключением стоящих при наивысших степенях равных P, делится без остатка на P. Делаем вывод, что и сумма таковых делится на P без остатка.
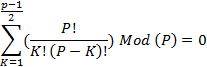 Тогда, сперва определим сумму всех биномиальных коэффициентов
Тогда, сперва определим сумму всех биномиальных коэффициентов
Поскольку, все коэффициенты, для нечётных степеней, нечётные и их количество нечётно, а сумма двух коэффициентов кратна 2, сгруппировав все элементы, определим максимальную степень сокращения.
(1+ 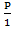 +(
+(  *
* 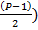 +(
+(  *
* 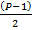 *
* 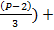 ...
...  (
(  *
* 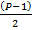 *
* 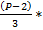 ...
... 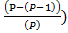 =>
=>
1 + 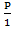 = 2*x1 =>
= 2*x1 =>
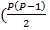 +
+ 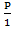 *
* 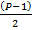 *
* 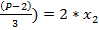 => (x1+ x2) = 2 x3 => 2(2(2(…(XP) = 2P =>
=> (x1+ x2) = 2 x3 => 2(2(2(…(XP) = 2P =>
А сумма уникальных биномиальных коэффициентов, для нечётных степеней в два раза меньше.
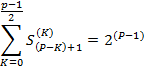
1+ 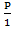 +(
+(  *
* 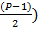 +(
+(  *
* 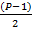 *
* 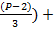 ...
...  (
(  *
* 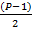 *
* 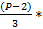 ...
... 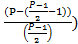 =
= 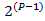
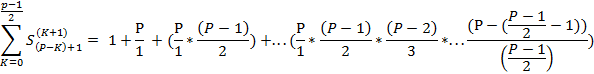
Перенеся первый коэффициент в правую сторону и разделив, обе части на P, мы определим сумму элементов, за исключением первого, сокращённых на P
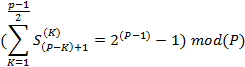
 + (
+ (  *
* 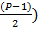 +(
+(  *
* 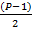 *
* 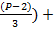 ...
...  (
(  *
* 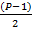 *
* 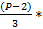 ...
... 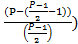 =
= 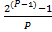
Сумма коэффициентов, кроме первого и второго, сокращённых на P
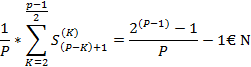
( 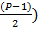 +(
+( 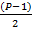 *
* 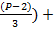 ...
...  (
( 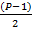 *
* 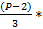 ...
... 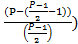 =
= 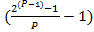 ? N
? N
В зависимости от количества уникальных биномиальных коэффициентов 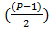 , количество элементов, оказывающих влияние на итоговый результат проверки числа на простоту, растёт. Количество которых равно, количеству уникальных биномиальных коэффициентов
, количество элементов, оказывающих влияние на итоговый результат проверки числа на простоту, растёт. Количество которых равно, количеству уникальных биномиальных коэффициентов 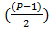
1+( 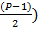 +(
+( 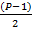 *
* 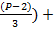 ...
...  (
( 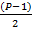 *
* 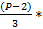 ...
... 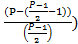 =
= 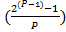 ? N
? N
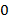 =
= 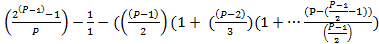
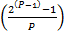 –
– 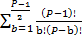 = 0
= 0 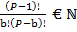
Т. е. Количество элементов, переносимых в правую часть уравнения, для сохранения истинности теста простоты, равняется 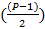 .
.
Рассмотрим несколько простых чисел P=3; 5
Для P=3
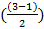 =1
=1
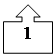 ( (
( ( 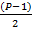 *
* 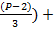 ...
...  (
( 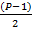 *
* 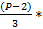 ...
... 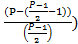 =
= 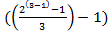 = 0
= 0
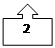 Для P=5
Для P=5
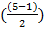 =2
=2
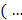 (
( 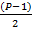 *
* 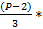 ...
... 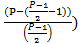 =
= 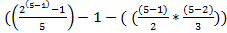 = 0
= 0
Зная число вычитаемых элементов, для обнуления уравнения, найдем (P(п)) - число проходящее тест простоты
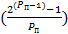 =
= 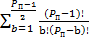
Поскольку количество вычитаемых элементов равно, количеству уникальных биномиальных коэффициентов, перепишем формулу.
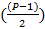 = b
= b
2b + 1=P(п)
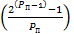 =
= 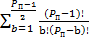 =1+(
=1+( 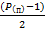 ) + (
) + ( 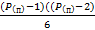 ) +…
) +…
Формула максимального значения уникального коэффициента, сокращённого на P(п)
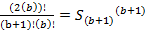 =
= 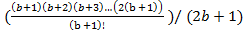
Зная всё выше перечисленное, выведем общую формулу простого числа
формула простого числа
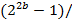 (
( 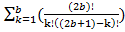 ) = P
) = P
b = (2N+1) + ( 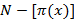 )
)
Однако за не имением, на данный момент, точной формулы дающей истинную оценку количества простых чисел 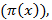 припишем формулу, опираясь на данные, доступные на данный момент, что значительно снизит достоверность данного алгоритма.
припишем формулу, опираясь на данные, доступные на данный момент, что значительно снизит достоверность данного алгоритма.
«Формальная» формула простого числа
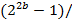 (
( 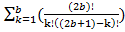 ) = Pф
) = Pф
b = N + Фс+ Фп
Фс ~ 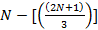 ; Фп
; Фп 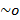
Где N – порядковый номер простого числа, Фс – количество чисел не удовлетворяющих малой теореме Ферма, на интервале от 1 до N. 3-отношения количества всех чисел, (на интервале от 1 до N) к количеству чисел вида
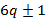 . Фп - количество псевдо-простых чисел, удовлетворяющих МТФ. []-округление вверх.
. Фп - количество псевдо-простых чисел, удовлетворяющих МТФ. []-округление вверх.
Выявим фактор простоты числа Фс
Для этого из количества чисел, проходящих проверку Фактора простоты, вычтем те, что её заведомо не пройдут.
Фс ~ 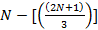
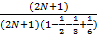 = 3
= 3
Найдем во сколько раз уменьшиться количество, потенциально составных чисел, при исключении чисел кратных 2 и 3. Поскольку в множестве потенциально простых, отсутствуют числа кратные 2 и 3. Для этого разделим общее количество простых чисел, на количество оставшихся чисел, после исключения 2 и 3. Количество оставшихся чисел, после исключения 2 и 3, определим вычтя из общего количества, числа кратные 2 и 3. Поскольку, вычитая числа кратные 2, мы уже вычли некоторые числа, которые пересекаются с числами кратными 3, т. е. числа кратные 6, вычитались дважды, возвращаем их.
Выявим фактор псевдо-простоты числа Фп
d – порядковый номер числа
| N | Pп=b+1 | Уровень проверки | 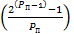 = = 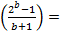 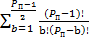
| b= |
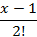
| 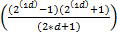
| 2d | ||
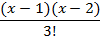
| 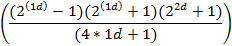
| 4d | ||
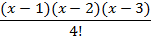
| 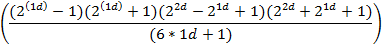
| 6d | ||
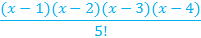
| 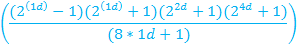
| 8d | ||
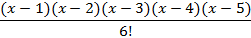
| 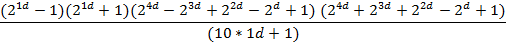
| 10d | ||
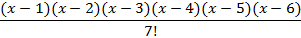
| 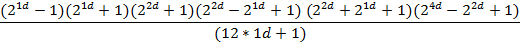
| 12d | ||
| 340d |
P(п)= 3
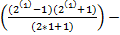
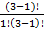 =
= 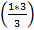 -1=0
-1=0
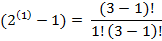
P(п)=5
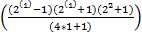 -
- 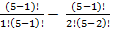 =
= 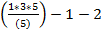 =0
=0
P(п)=7
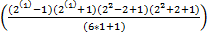 -
- 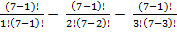 =
= 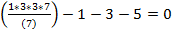
P(п)=9
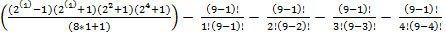 =
= 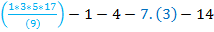
P(п)=11
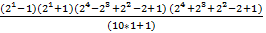 -
- 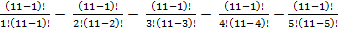 =
= 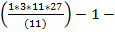 5 -15 -30-42=0
5 -15 -30-42=0
P(п)=13
(21-1)(21+1)(22+1)(22-2+1) (22+2+1)(24-22+1) - 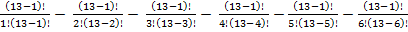 =
=
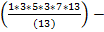 1-6-22-55-99-132=0
1-6-22-55-99-132=0
Вывод: все поставленные задачи были решены в ходе данной работы.
Примечание:
Фс – точность вычисления, количества чисел не удовлетворяющих малой теореме Ферма, на интервале от 1 до N, может быть повышена до абсолютной.
Вычисление Pф – может быть существенно облегчено, путём взаимного сокращения, частного и делителя
Список литературы и интернет источников:
https: //ru. wikipedia. org/wiki/%D0%A2%D0%B5%D1%81%D1%82_%D0%90%D0%B3%D1%80%D0%B0%D0%B2%D0%B0%D0%BB%D0%B0_%E2%80%94_%D0%9A%D0%B0%D1%8F%D0%BB%D0%B0_%E2%80%94_%D0%A1%D0%B0%D0%BA%D1%81%D0%B5%D0%BD%D1%8B
https: //ru. wikipedia. org/wiki/%D0%91%D0%B8%D0%BD%D0%BE%D0%BC_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0
https: //ru. wikipedia. org/wiki/%D0%9C%D0%B0%D0%BB%D0%B0%D1%8F_%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%A4%D0%B5%D1%80%D0%BC%D0%B0
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|