
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание 3.6. Таблица 3.5. Задание 3.7. Таблица 3.6. Задание 3.8. Таблица 3.7. Задание 3.9. Задание 3.10. Таблица 3.8. Задание 3.11. Таблица 3.9
Задание 3. 6
Определить по представленному коммерческому банку в целом: средний размер вклада и среднее число вкладчиков в отделениях.
Таблица 3. 5
Показатели деятельности коммерческого банка
| Номер филиала | Число отделений в филиалах | Средний размер вклада, тыс. руб. | Среднее число вкладчиков в каждом отделении |
Задание 3. 7
По данным о реализации товара по трем коммерческим магазинам представленным в таблице 3. 6, рассчитать среднюю цену товара.
Таблица 3. 6
Реализация товара по трем коммерческим магазинам
| Номер магазина | Цена товара, руб. /кг | Выручка от реализации, руб. | |
Задание 3. 8
Исходя из имеющихся данных, определить среднюю стоимость путевки турфирмы в 1 полугодии, во 2 полугодии и за год.
Таблица 3. 7
Средняя стоимость путевок
| Номер филиала | 1 полугодие | 2 полугодие | ||||
| Объем турпотока, чел. | Средняя стоимость путевки, руб. | Средняя стоимость путевки, руб. | Выручка от путевок, тыс. руб. | |||
Задание 3. 9
Есть три квадрата со сторонами 10, 20 и 30 см. Вычислить среднюю сторону квадратов.
Задание 3. 10
Рассчитать среднюю цену тура по трём маршрутам исходя из имеющихся данных
Таблица 3. 8
Средняя цена тура и выручка
| Номер маршрута | Средняя цена тура, тыс. руб. | Выручка от продажи турпродукта, тыс. руб. | |
Задание 3. 11
Определить среднюю стоимость 1 дня тура
Таблица 3. 9
Однодневная стоимость тура и его продолжительность
| № маршрута | Стоимость 1 дня, руб. | Продолжительность тура, дней | |
Тема 4: Показатели вариации
Термин “вариация” происходит от латинского слова variation – изменение, колеблемость, различие.
Вариация – это различие между индивидуальными явлениями.
Степень близости индивидуальных значений признака (вариант) к средней измеряется рядом абсолютных, средних и относительных статистических показателей. К ним относятся
Абсолютные показатели:
· размах вариации: R=Хmax-Xmin
Средние показатели:
· среднее линейное отклонение,
· для несгруппированных данных:
· для сгруппированных данных:
· дисперсия – средний квадрат отклонения от их средней величины
· для несгруппированных данных: Д=
· для сгруппированных данных: Д=
Если совокупность разбита на группы по какому-либо признаку, то можно определить дисперсию общую, гмежгрупповую (факторную) и внутригрупповую (случайную).
· среднее квадратическое отклонение – корень из дисперсии:
Относительные показатели:
· относительный размах вариации: VR =
· относительное линейное отклонение: VL =
· коэффициент вариации: V=
При этом совокупность считается однородной, если V не превышает 33%/
К показателям формы распределения относятся асимметрия и эксцесс.
Симметричным называется распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой.
Если распределение симметричное, то =Мо=Ме
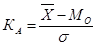 Коэффициент асимметрии Пирсона:
Коэффициент асимметрии Пирсона:
Если Ка=0- ряд распределения симметричен, Ка> 0-скошенность ряда правосторонняя, Ка< 0-скошенность ряда левосторонняя.
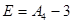 Эксцесс – характеристика островершинности и крутизны распределения.
Эксцесс – характеристика островершинности и крутизны распределения.
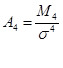 Эксцесс распределения:
Эксцесс распределения:
где А4- нормированный момент четвертого порядка:
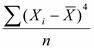 где М4- центральный момент четвертого порядка:
где М4- центральный момент четвертого порядка:
по несгрупированным данным: М4=
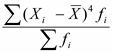 по сгрупированным данным: М4=
по сгрупированным данным: М4=
Если Е = 0 – распределение нормальное, если Е > 0 - островершинное, Е < 0 – плосковершинное.
Студент должен
знать:
· Сущность вариации;
· показатели вариации и способы их расчета;
· виды дисперсий и правило сложения дисперсий
уметь:
· Правильно рассчитывать показатели вариации;
· Интерпретировать полученные данные
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|