4. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И НУЛИ ФУНКЦИИ.

4. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И НУЛИ ФУНКЦИИ.

Значения аргумента х из области определения функции у = f (х), при которых соответствующие значения функции равны нулю, называются нулями функции.

Значения аргумента, при которых функция обращается в нуль, - это абсциссы точек пересечения графика функции с осью Ох.

Числовые промежутки, на которых функция сохраняет свой знак, т. е. остается положительной или отрицательной, называются промежутками знакопостоянства функции.

Промежутки знакопостоянства – это промежутки между нулями функции, т. к. при переходе через нуль функция меняет свой знак на противоположный. О промежутках знакопостоянства и нулях функции легко судить по ее графику.

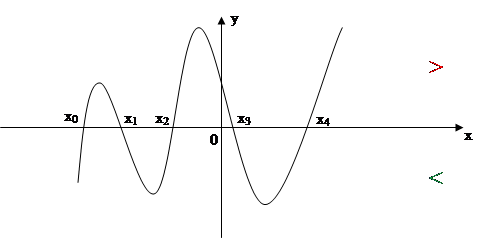
x₀, x₁, x₂, x₃, x₄ – нули функции;

f(x) > 0 на (x₀; x₁); (x₂; x₃); (x₄; +¥ 0 - промежутки знакопостоянства,

f(x) < 0 на (-¥; x₀); (x₁; x₂); (x₃; x₄) - промежутки знакопостоянства.

⇐ Предыдущая 1 23