Хелпикс

Главная

Контакты

Случайная статья



1. «ОПРЕДЕЛЕНИЕ ФУНКЦИИ»

Стр 1 из 3Следующая ⇒


 

ЗАДАНИЕ::: ИЗУЧИТЬ МАТЕРИАЛ И СОСТАВИТЬ КРАТКИЙ КОНСПЕКТ.

 

 « ОПРЕДЕЛЕНИЕ ФУНКЦИИ. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ».

1. «ОПРЕДЕЛЕНИЕ ФУНКЦИИ»

 

Зависимость переменной у от переменой х, при которой каждому значению переменной х соответствует единственное значение переменной у, называется функциональной зависимостью или функцией.

- общее обозначение функциональной зависимости, где

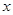 - независимая переменная или аргумент;

- зависимая переменная или функция.

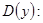 область определения функции – те значения, которые может принимать переменная 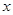(аргумент).

: множество значений функции – соответствующие значения функции (переменной ).

 

 !!! !!! Для нахождения области определения функции, заданной аналитически  ( с помощью формулы), используем следующие положения: 1) если формула содержит радикал ( 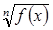) с четным показателем n, то подкоренное выражение может быть только числом неотрицательным ( );

                 2) если речь идет о любой из логарифмических функций ( 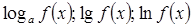), то функция  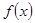может быть только положительной на основании определения логарифма( 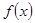> 0);

                  3) если формула, задающая функцию, есть дробь, в знаменателе которой стоит выражение, содержащее переменную, то знаменатель не может быть равен нулю;

                 4) для обратных тригонометрических функций 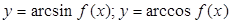 по свойствам обратных функций ;

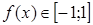               5) для тригонометрической функции 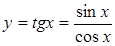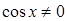, т. е., .

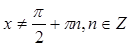                6)  для тригонометрической функции 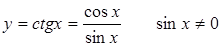, т. е., .

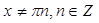                      7) во всех остальных случаях область определения функции есть все множество действительных чисел, т. е., .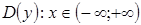

 

 у
Графиком функции называется множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты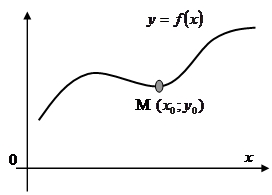

соответствующим значениям функции, т. е.,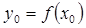

 

 

                             


123Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.