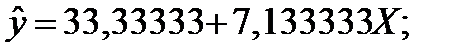Хід роботи

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

Міністерство освіти і науки України

Національний технічний університет України

«Київський політехнічний інститут»

Факультет менеджменту та маркетингу

Кафедра математичного моделювання економічних систем

Комп’ютерний практикум № 1

з дисципліни «Економетрика»

на тему: «Визначення оцінок параметрів емпіричних функцій регресії, що моделюють монотонний процес»

Виконав:

студент групи УК-21

Каплун Олексій

Прийняв:

доцент кафедри ММЕС Фартушний І. Д.

Київ – 2014

Тема: Визначення оцінок параметрів емпіричних функцій регресії, що моделюють монотонний процес

Ціль роботи: Не знаючи оцінок, вибрати більш підходящу із 9-ти функцій, як функцію регресії.

При моделюванні монотонних процесів (зростаючих або спадаючих), коли число спостережень 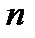невелике і невідомо, чиє асимптотичний рівень і перегин у тенденції зміни результативної змінної 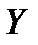з ростом пояснюючої змінної 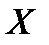може бути використана одна з наступних функцій регресії, які залежать від двох параметрів:

;

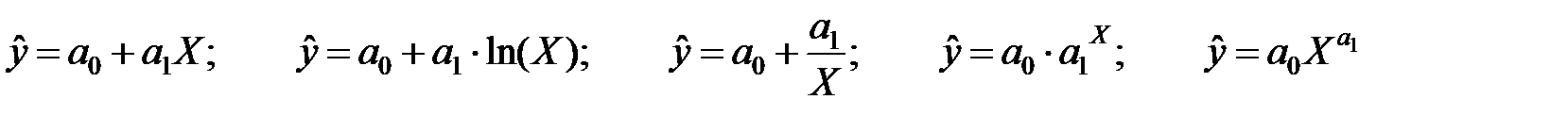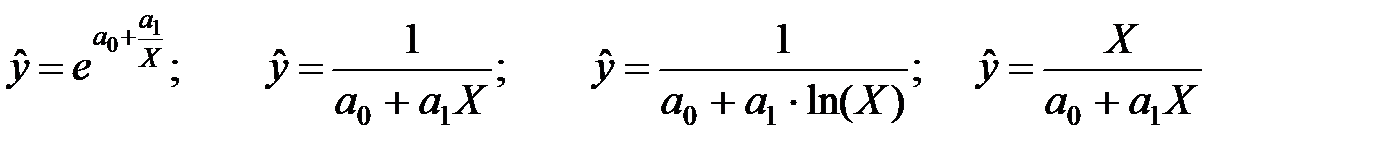Завдання до комп’ютерного практикуму: Продемонструвати методику застосування методу найменших квадратів для всіх дев’яти монотонних залежностей на прикладі моделювання динаміки росту курсу акцій:

Таблиця 1

t
Y(t)

з наступним аналізом побудованих моделей і порівнянням отриманих результатів з висновками, заснованими на критерію.

Хід роботи

Для кожної з поданих функцій регресії потрібно оцінити параметри а0 та а1, після чого потрібно визначити суму квадратів відхилень значень функції регресії у точках від значень функції, заданої у таблиці 1. Та функція регресії, для якої сума квадратів відхилень буде найменшою, вважається такою, яка найбільш точно відтворює залежність між даними, які подані у таблиці 1.

Оцінки параметрів та сума квадратів відхилень подані у таблицях 2-11.

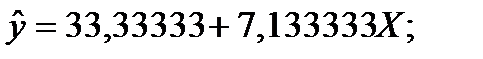
x	y	x^2	x*y	y^	(y-y^)^2
				40, 46667	6, 084444
				47, 6	0, 36
				54, 73333	0, 071111
				61, 86667	4, 551111

				76, 13333	14, 95111
				83, 26667	7, 471111
				90, 4	1, 96
				97, 53333	12, 48444
					48, 93333

Таблиця 2

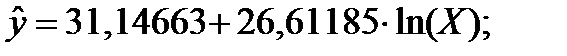
x

y

lnx

(lnx)^2

y*lnx

y^

(y-y^)^2

31, 14663

46, 96873

0, 693147

0, 480453

32, 57792

49, 59256

6, 721356

1, 098612

1, 206949

60, 42368

60, 38274

28, 97385

1, 386294

1, 921812

88, 72284

68, 03849

16, 3094

1, 609438

2, 59029

109, 4418

73, 97675

35, 72158

1, 791759

3, 210402

143, 3408

78, 82867

1, 37202

1, 94591

3, 786566

167, 3483

82, 9309

9, 419356

2, 079442

4, 324077

185, 0703

86, 48442

6, 328138

2, 197225

4, 827796

206, 5391

89, 61885

19, 19451

12, 80183

22, 34835

993, 4646

171, 0089

Таблиця 3

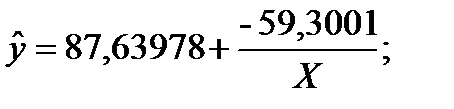
x

y

1/x

1/x^2

y/x

y^

(y-y^)^2

28, 33972

93, 3211

0, 5

0, 25

23, 5

57, 98975

120, 7745

0, 333333

0, 111111

18, 33333

67, 87309

165, 7164

0, 25

0, 0625

72, 81476

77, 70002

0, 2

0, 04

13, 6

75, 77976

60, 52474

0, 166667

0, 027778

13, 33333

77, 75643

5, 033592

0, 142857

0, 020408

12, 28571

79, 16834

46, 67159

0, 125

0, 015625

11, 125

80, 22727

76, 96081

0, 111111

0, 012346

10, 44444

81, 05088

167, 6797

2, 828968

1, 539768

156, 6218

814, 3825

Таблиця 4

Таблиця 5

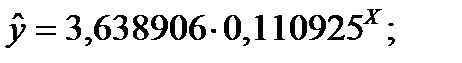
x

y

lny

x^2

x*lny

y^

(y-y^)^2

3, 637586

3, 637586

42, 5139

20, 37527

3, 850148

7, 700295

47, 50123

0, 25123

4, 007333

12, 022

53, 07363

3, 710917

4, 158883

16, 63553

59, 29972

22, 09259

4, 219508

21, 09754

66, 25621

3, 040802

4, 382027

26, 29216

74, 02877

35, 65564

4, 454347

31, 18043

82, 71312

10, 80355

4, 488636

35, 90909

92, 41625

11, 67076

4, 543295

40, 88965

103, 2577

85, 70418

37, 74176

195, 3643

193, 305

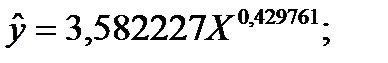
x

y

lnx

(lnx)^2

lny

lnx*lny

y^

(y-y^)^2

3, 637586

35, 95351

Таблиця 6

4, 188138

0, 693147

0, 480453

3, 850148

2, 668719

48, 42974

2, 044155

1, 098612

1, 206949

4, 007333

4, 402505

57, 64866

7, 015423

1, 386294

1, 921812

4, 158883

5, 765436

65, 23535

1, 526098

1, 609438

2, 59029

4, 219508

6, 791036

71, 80111

14, 44842

1, 791759

3, 210402

4, 382027

7, 851538

77, 65334

5, 506816

1, 94591

3, 786566

4, 454347

8, 66776

82, 97194

9, 169151

2, 079442

4, 324077

4, 488636

9, 333857

87, 87269

1, 270835

2, 197225

4, 827796

4, 543295

9, 982639

92, 43517

2, 448686

12, 80183

22, 34835

37, 74176

55, 46349

47, 61772

Таблиця 7

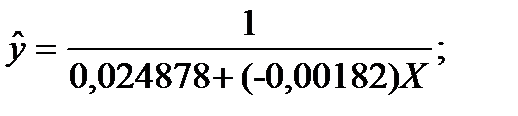
x

y

x^2

1/y

x/y

y^

(y-y^)^2

0, 026316

0, 026316

43, 36387

28, 77106

0, 021277

0, 042553

47, 07449

0, 005548

0, 018182

0, 054545

51, 47956

12, 39348

0, 015625

0, 0625

56, 79418

51, 9239

0, 014706

0, 073529

63, 33245

21, 78602

0, 0125

0, 075

71, 57198

71, 03157

0, 011628

0, 081395

82, 27606

13, 86772

0, 011236

0, 089888

96, 74494

59, 98402

0, 010638

0, 095745

117, 3886

547, 0276

0, 142107

0, 601472

806, 7909

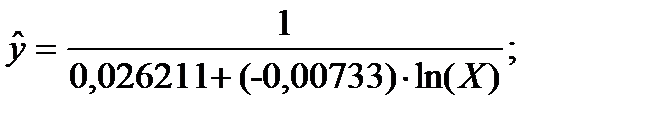
x

y

lnx

(lnx)^2

1/y

lnx/y

y^

(y-y^)^2

0, 026316

38, 15179

0, 023039

0, 693147

0, 480453

0, 021277

0, 014748

47, 31992

0, 102348

1, 098612

1, 206949

0, 018182

0, 019975

55, 05968

Таблиця 8

0, 003562

1, 386294

1, 921812

0, 015625

0, 021661

62, 28819

2, 930285

1, 609438

2, 59029

0, 014706

0, 023668

69, 35031

1, 823342

1, 791759

3, 210402

0, 0125

0, 022397

76, 43059

12, 7407

1, 94591

3, 786566

0, 011628

0, 022627

83, 65133

5, 516231

2, 079442

4, 324077

0, 011236

0, 023365

91, 10734

4, 440877

2, 197225

4, 827796

0, 010638

0, 023375

98, 88139

23, 82794

12, 80183

22, 34835

0, 142107

0, 171815

51, 40832

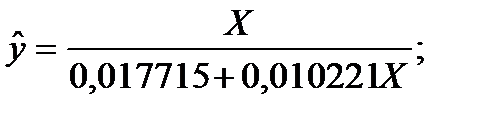
x

y

1/y

1/x^2

1/(x*y)

1/x

y^

(y-y^)^2

0, 026316

0, 026316

35, 7953

4, 860714

0, 021277

0, 25

0, 010638

0, 5

52, 41387

29, 30998

0, 018182

0, 111111

0, 006061

0, 333333

62, 01031

49, 14451

0, 015625

0, 0625

0, 003906

0, 25

68, 25909

18, 13981

0, 014706

0, 04

0, 002941

0, 2

72, 65175

21, 63878

0, 0125

0, 027778

0, 002083

0, 166667

75, 90836

16, 7415

0, 011628

0, 020408

0, 001661

0, 142857

78, 41917

57, 46893

0, 011236

0, 015625

0, 001404

0, 125

80, 41406

73, 7184

0, 010638

0, 012346

0, 001182

0, 111111

82, 03722

143, 1081

0, 142107

1, 539768

0, 056193

2, 828968

414, 1307

Таблиця 9

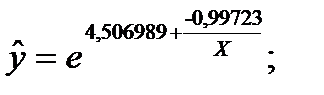
x

y

1/x

lny

1/x^2

lny/x

y^

Таблиця 10

(y-y^)^2

3, 637586

3, 637586

33, 44015

20, 79227

0, 5

3, 850148

0, 25

1, 925074

55, 05722

64, 91879

0, 333333

4, 007333

0, 111111

1, 335778

65, 01242

100, 2485

0, 25

4, 158883

0, 0625

1, 039721

70, 64596

44, 16878

0, 2

4, 219508

0, 04

0, 843902

74, 25778

39, 15977

0, 166667

4, 382027

0, 027778

0, 730338

76, 76767

10, 44797

0, 142857

4, 454347

0, 020408

0, 636335

78, 61222

54, 57927

0, 125

4, 488636

0, 015625

0, 56108

80, 02466

80, 55666

0, 111111

4, 543295

0, 012346

0, 504811

81, 14075

165, 3603

2, 828968

37, 74176

1, 539768

11, 21462

580, 2323

Номер функції

Вид функції

Оцінки параметрів

Сумма відхиленнь

1 –

Лінійна

y=a0+a1*t

48, 93333

2 - Логарифмічна

y=a0+a1*ln(t)

171, 0089

3 - Гіперболічна

y=a0+a1/t

814, 3825

4 - Степенева

y=a0*(a1)^(t)

193, 305

5 - Показникова

y=a0*(t)^(a1)

47, 61772

y=(e)^(a0+a1/t)

580, 2323

y=1/(a0+a1*t)

806, 7909

y=1/(a0+a1*ln(t))

51, 40832

y=t/(a0+a1*t)

414, 1307

Таблиця 11

Висновок. Отже, в ході виконання роботи за допомогою методу найменших квадратів ми визначили наближення функціональної залежності зміни результативної змінної 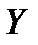з ростом пояснюючої змінної 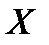, тобто знайшли функцію регресії, яка найбільш точно описує тенденцію зміни даних. Розглянувши всі можливі випадки виявилось, що функції вигляду y=a0+a1*t, y=a0*(t)^(a1), y=1/(a0+a1*ln(t)) найбільш точно описують задані величини, тобто для них сума квадратів відхилень найменша.

⇐ Предыдущая 1 234 Следующая ⇒