Хелпикс

Главная

Контакты

Случайная статья



I способ. 2 страница

⇐ ПредыдущаяСтр 3 из 5Следующая ⇒


  .

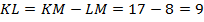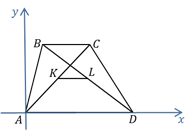
II способ. Воспользуемся методом координат. Направим оси координат так, чтобы основание  трапеции . Тогда 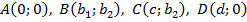. Так как точка  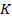– середина отрезка 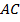, а точка  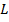– середина отрезка 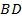, то по формулам координат середины отрезка, находим координаты этих точек.

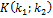
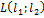
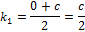
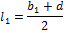
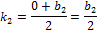
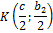
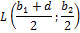
По формуле расстояния между точками, находим длины отрезков 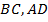 и .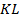

.

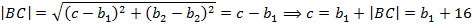
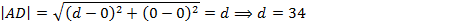
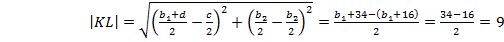Ответ: .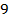

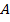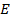17. (316359) Биссектриса угла  параллелограмма  пересекает сторону  в точке . Найдите площадь параллелограмма , если .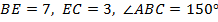

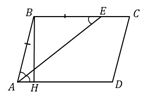Решение.

I способ. Так как 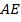 – биссектриса 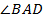, то .

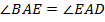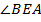 и 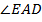 – внутренние накрест лежащие при параллельных прямых  и , значит, 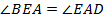. Поэтому 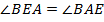. Следовательно,  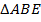равнобедренный, и .

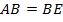Опустим высоту параллелограмма 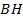 на сторону . Получили прямоугольный треугольник 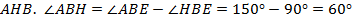. По сумме углов треугольника, 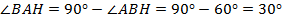. В прямоугольном треугольнике напротив угла, равного 30°, лежит катет, равный половине гипотенузы, т. е. 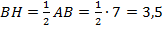. Теперь найдём площадь параллелограмма:

  .

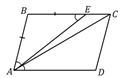
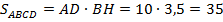II способ. Начальные рассуждения такие же, как в первом способе.

Так как 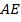 – биссектриса 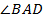, то .

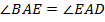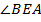 и 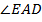 – внутренние накрест лежащие при параллельных прямых, значит, 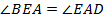. Поэтому  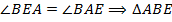равнобедренный, и .

.

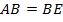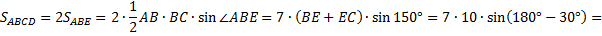
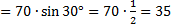Ответ: .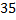

18. (333130) Биссектрисы углов 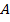 и 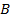 при боковой стороне  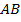трапеции  пересекаются в точке 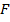. Найдите 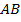, если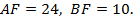

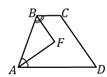Решение.

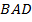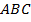Углы  и  трапеции  – внутренние односторонние при параллельных прямых  и . Значит, их сумма равна 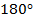, т. е.

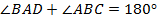  . Т. к.  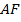– биссектриса 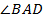, то 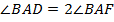. Аналогично,  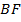– биссектриса 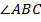, значит, 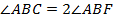. Тогда,

.

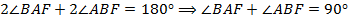Из 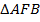, по сумме углов треугольника, находим:

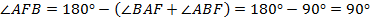  , т. е.  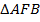– прямоугольный.

По теореме Пифагора:

.

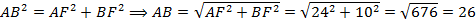Ответ: .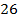

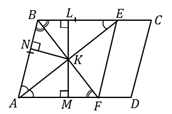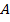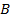19. (339709) Биссектрисы углов  и  параллелограмма  пересекаются в точке 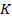. Найдите площадь параллелограмма, если 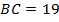, а расстояние от точки  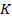до стороны  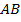равно .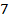

Решение.

Так как 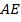 – биссектриса 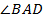, то .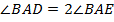

Так как 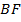 – биссектриса 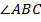, то .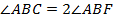

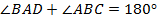 (по свойству односторонних углов при параллельных прямых  и ). Тогда

.

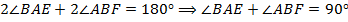Из 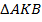, по свойству углов треугольника, находим угол .

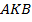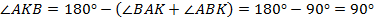, т. е.  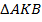– прямоугольный. Соответственно,  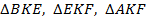– прямоугольные.

Проведём высоту параллелограмма через точку .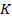

Рассмотрим 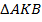 и .

 по II признаку равенства треугольников. Значит, все элементы у них равны, т. е. .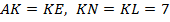

Рассмотрим  и .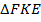

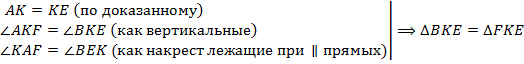 по I признаку равенства треугольников, следовательно, .

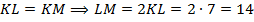Находим площадь параллелограмма.

.

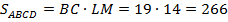Ответ: .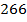

 

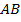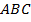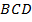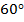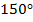20. (351992) Найдите боковую сторону  трапеции , если углы  и  соответственно равны  и , а .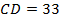

Решение.

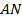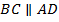Проведём высоту  к стороне  и высоту  к стороне . Так как , то .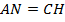

В .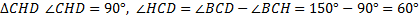

Тогда, по сумме углов треугольника, 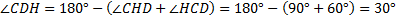. Используя свойство угла, равного 30°, в прямоугольном треугольнике («в прямоугольном треугольнике напротив угла, равного 30°, находится катет, равный половине гипотенузы), находим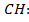 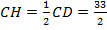  . Значит, . В .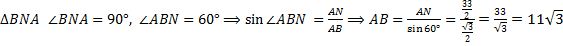

Ответ: .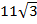

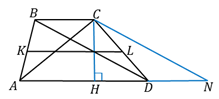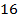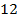21.  (353511) Найдите площадь трапеции, диагонали которой равны  и , а средняя линия равна .

Решение.

I способ. Пусть 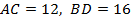 – диагонали трапеции , а  – средняя линия этой трапеции. Проведём высоту  к основанию  и прямую 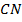, параллельную 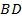. Получили параллелограмм 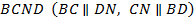. Так как у параллелограмма противолежащие стороны равны, то 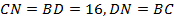. Тогда . Здесь мы использовали свойство средней линии трапеции: «Средняя линия трапеции параллельна основаниям и равна их полусумме», т. е. 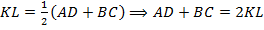. Поскольку в  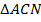известны все стороны, то для нахождения его площади можно использовать формулу Герона.

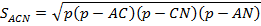
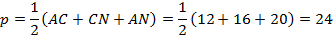
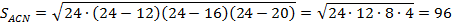
Теперь, площадь этого же треугольника найдём по другой формуле:

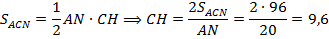
Находим площадь трапеции

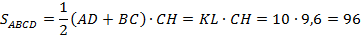
II способ. Решим эту же задачу методом координат. Направим оси координат так, чтобы сторона  лежала на оси Ох. Проведём высоту 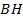 с основанию . Введём координаты точек: 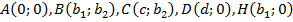. Так как  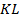– средняя линия трапеции, то найдём координаты точек  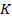и 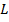 по формулам координат середины отрезков  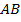и 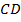 соответственно.

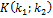
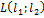
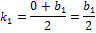
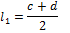
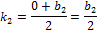
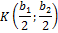
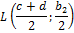
Теперь запишем с помощью координат известные нам длины отрезков и длину отрезка .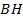

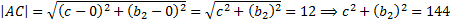
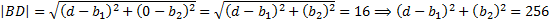
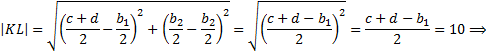
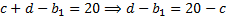
Значит,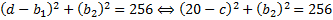               

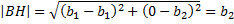
Значит, для нахождения высоты 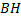 нам достаточно найти координату .

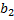Составим систему уравнений:

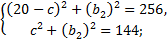
Вычтем из первого уравнения второе:

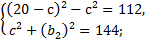
Решим первое уравнение: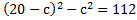            

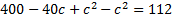
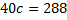
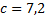
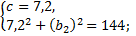
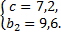
Значит, . Находим площадь трапеции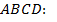

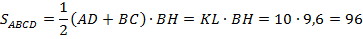
Ответ: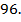

 

ЗАДАЧИ

ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. (311560) Основания равнобедренной трапеции равны 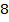 и 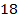, а периметр равен . Найдите площадь трапеции.

2. (324779) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 14, а одна из диагоналей ромба равна 56. Найдите углы ромба.

3. (324780) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 13, а одна из диагоналей ромба равна 52. Найдите углы ромба.

4. (324781) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 10, а одна из диагоналей ромба равна 40. Найдите углы ромба.

5. (324782) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 17, а одна из диагоналей ромба равна 68. Найдите углы ромба.

6. (324783) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 18, а одна из диагоналей ромба равна 72. Найдите углы ромба.

7. (324784, 355302) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 15, а одна из диагоналей ромба равна 60. Найдите углы ромба.

8. (324785, 355427) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 12, а одна из диагоналей ромба равна 48. Найдите углы ромба.

9. (324786) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 16, а одна из диагоналей ромба равна 64. Найдите углы ромба.

10. (324787) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 11, а одна из диагоналей ромба равна 44. Найдите углы ромба.

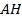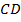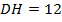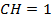11. (341290) Высота  ромба  делит сторону  на отрезки  и . Найдите высоту ромба.

12. (311572) Периметр прямоугольника равен 30, а диагональ равна 14. Найдите площадь этого прямоугольника.

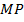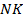13. (311699) Прямая, параллельная основаниям  и  трапеции 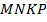, проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны  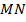и 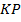 в точках  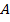и 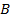 соответственно. Найдите длину отрезка 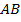, если .

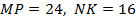14. (311698) Прямая, параллельная основаниям  и  трапеции , проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны 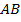 и 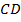 в точках  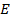и 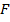 соответственно. Найдите длину отрезка 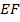, если .

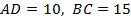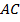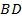15. (311709) Диагонали  и  трапеции  пересекаются в точке 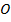. Площади треугольников  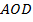и 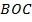 равны соответственно  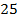см2 и 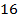 см2. Найдите площадь трапеции.

16. (348450) В выпуклом четырёхугольнике 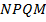 диагональ  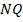является биссектрисой угла  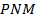и пересекается с диагональю  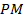в точке 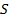. Найдите 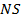, если известно, что около четырёхугольника  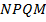можно описать окружность,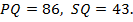

17. (348979) В выпуклом четырёхугольнике 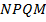 диагональ  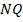является биссектрисой угла  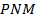и пересекается с диагональю  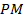в точке 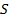. Найдите 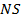, если известно, что около четырёхугольника  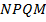можно описать окружность,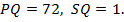

18. (349411) В выпуклом четырёхугольнике 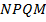 диагональ  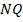является биссектрисой угла  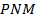и пересекается с диагональю  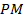в точке 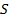. Найдите 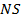, если известно, что около четырёхугольника  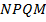можно описать окружность,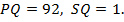

19. (349474) В выпуклом четырёхугольнике 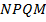 диагональ  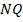является биссектрисой угла  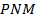и пересекается с диагональю  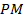в точке 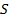. Найдите 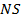, если известно, что около четырёхугольника  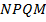можно описать окружность,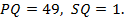


⇐ Предыдущая12345Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.