
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Классная работа «Четырёхугольники»
Классная работа «Четырёхугольники»
ЗАДАНИЕ 24 ОГЭ.
ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ВЫЧИСЛЕНИЕ.
ЧЕТЫРЁХУГОЛЬНИКИ.
1. 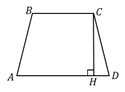 (311249) Основания равнобедренной трапеции равны
(311249) Основания равнобедренной трапеции равны 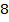 и
и 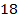 , а периметр равен
, а периметр равен 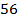 . Найдите площадь трапеции.
. Найдите площадь трапеции.
Решение.
Так как трапеция равнобедренная, то 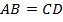 , а значит, периметр имеет вид:
, а значит, периметр имеет вид: 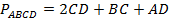 . Выражаем отсюда сторону
. Выражаем отсюда сторону 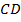 .
.
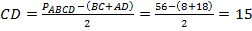 .
.
Опустим высоту  . В силу равнобедренности трапеции,
. В силу равнобедренности трапеции, 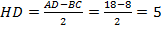 .
.
Из 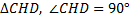 , по теореме Пифагора
, по теореме Пифагора 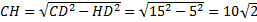
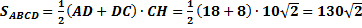 .
.
Ответ: .
2. 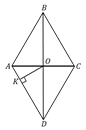 (324778) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
(324778) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
Решение.
I способ . Опустим перпендикуляр 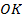 к стороне
к стороне  . Пусть
. Пусть 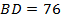 . По свойству диагоналей ромба («диагонали ромба пересекаются и точкой пересечения делятся пополам»)
. По свойству диагоналей ромба («диагонали ромба пересекаются и точкой пересечения делятся пополам») 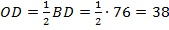 .
.
Из 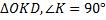 , по теореме Пифагора:
, по теореме Пифагора: 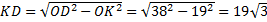 .
.
Так как высота прямоугольного треугольника, опущенная из прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу, то:
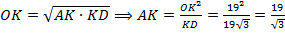 . Тогда
. Тогда 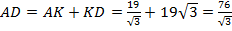 .
.
Т. к. у ромба все стороны равны, то 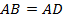 . Из
. Из 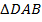 по теореме косинусов:
по теореме косинусов:
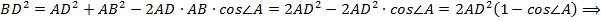
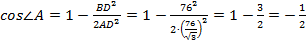 . Т. к. значение косинуса отрицательно, то угол
. Т. к. значение косинуса отрицательно, то угол 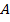 – тупой. Используя формулу приведения для косинуса (
– тупой. Используя формулу приведения для косинуса ( 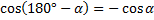 ), и учитывая, что
), и учитывая, что 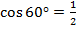 , определяем, что
, определяем, что 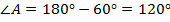 .
.
У ромба соседние углы являются внутренними односторонними при параллельных прямых, значит, в сумме они дают 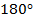 , т. е.
, т. е. 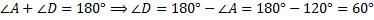 .
.
Противоположные углы равны, значит, 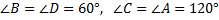 .
.
II способ. Опустим перпендикуляр 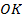 . Пусть
. Пусть 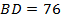 . По свойству диагоналей ромба («диагонали ромба пересекаются и точкой пересечения делятся пополам»)
. По свойству диагоналей ромба («диагонали ромба пересекаются и точкой пересечения делятся пополам») 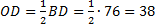 . В
. В 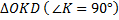 найдём
найдём 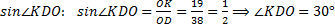 .
.
Так как диагонали ромба являются биссектрисами углов, то 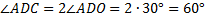 .
.
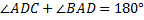 (по свойству внутренних односторонних углов при параллельных прямых)
(по свойству внутренних односторонних углов при параллельных прямых) 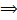
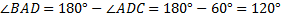 .
.
Противоположные углы ромба равны, значит, 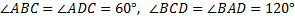 .
.
Ответ:  .
.
3. (340934) В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 8.
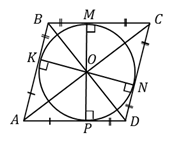 Решение.
Решение.
I способ. Окружность вписана в параллелограмм  , значит, она касается сторон
, значит, она касается сторон 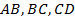 и
и  в точках
в точках 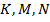 и
и  соответственно, т. е. стороны параллелограмма являются касательными к окружности. По свойству: «отрезки касательных, проведённых из одной точки, равны» заключаем, что:
соответственно, т. е. стороны параллелограмма являются касательными к окружности. По свойству: «отрезки касательных, проведённых из одной точки, равны» заключаем, что: 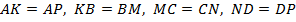 .
.
Рассмотрим 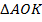 и
и 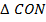 .
.
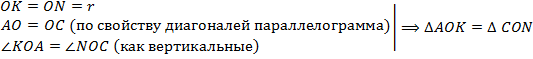 по I признаку равенства треугольников. Следовательно,
по I признаку равенства треугольников. Следовательно, 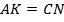 , но
, но 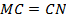 , значит,
, значит,  . Кроме того,
. Кроме того, 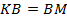 , значит,
, значит, 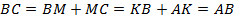 , т. е. данный параллелограмм является ромбом и все стороны у него равны. Тогда,
, т. е. данный параллелограмм является ромбом и все стороны у него равны. Тогда, 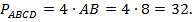

II способ. Этот способ гораздо короче и использует признак описанного четырёхугольника: «Суммы противоположных сторон описанного четырёхугольника равны», т. е. 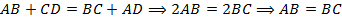 , т. е. т. е. данный параллелограмм является ромбом и все стороны у него равны. Тогда,
, т. е. т. е. данный параллелограмм является ромбом и все стороны у него равны. Тогда, 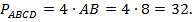
Ответ: 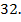
4.  (341285) Высота
(341285) Высота 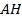 ромба
ромба  делит сторону
делит сторону 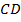 на отрезки
на отрезки 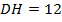 и
и  . Найдите высоту ромба.
. Найдите высоту ромба.
Решение.
Так как у ромба все стороны равны, то 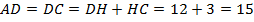 .
.
Из 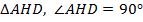 по теореме Пифагора:
по теореме Пифагора: 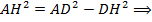
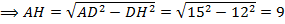 .
.
Ответ: 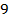 .
.
5. 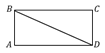 (311566) Периметр прямоугольника равен 56, а диагональ равна 27. Найдите площадь этого прямоугольника.
(311566) Периметр прямоугольника равен 56, а диагональ равна 27. Найдите площадь этого прямоугольника.
Решение.
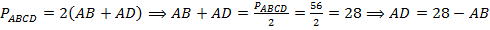 .
.
Тогда площадь прямоугольника равна: 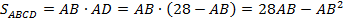 .
.
Из 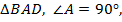 по теореме Пифагора:
по теореме Пифагора: 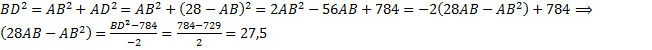 .
.
Значит,  .
.
Ответ:  .
.
6. (311671) Прямая, параллельная основаниям 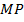 и
и 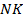 трапеции
трапеции 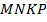 , проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны
, проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны 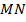 и
и 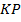 в точках
в точках 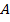 и
и 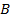 соответственно. Найдите длину отрезка
соответственно. Найдите длину отрезка 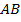 , если
, если 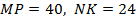 .
.
 Решение.
Решение.
I способ. Воспользуемся свойством трапеции: «Отрезок, параллельный основаниям, проходящий через точку пересечения диагоналей, делится ею пополам и равен отношению удвоенного произведения оснований к сумме оснований», т. е. 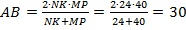 .
.
II способ. Этот способ для тех, кто не помнит свойство трапеции, описанное в I способе.
Воспользуемся другим свойством: «Точка пересечения диагоналей трапеции делит её на два подобных треугольника, содержащих основания, и два равновеликих треугольника, содержащих боковые стороны», т. е. 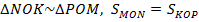 . Если и это свойство не всплывает в памяти, то легко доказать подобие треугольников
. Если и это свойство не всплывает в памяти, то легко доказать подобие треугольников 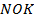 и
и 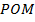 .
.
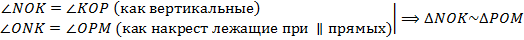 по I признаку подобия треугольников. Значит, стороны у этих треугольников пропорциональны, т. е.
по I признаку подобия треугольников. Значит, стороны у этих треугольников пропорциональны, т. е.
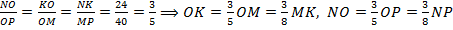 .
.
Рассмотрим  и
и  .
.
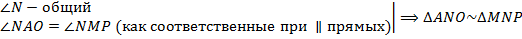 по I признаку подобия треугольников, значит,
по I признаку подобия треугольников, значит, 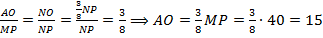 .
.
Аналогично, 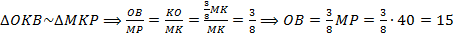 .
.
Тогда, 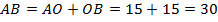 .
.
Ответ: 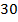 .
.
7.  (311666) Диагонали
(311666) Диагонали 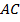 и
и 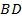 трапеции
трапеции  пересекаются в точке
пересекаются в точке 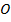 . Площади треугольников
. Площади треугольников 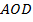 и
и 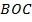 равны соответственно
равны соответственно 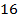 см2 и
см2 и 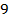 см2. Найдите площадь трапеции.
см2. Найдите площадь трапеции.
Решение.
Рассмотрим  и
и 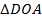 .
.
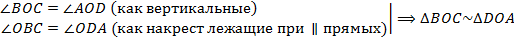 по I признаку подобия треугольников. Значит, их площади относятся, как квадрат коэффициента подобия, т. е.
по I признаку подобия треугольников. Значит, их площади относятся, как квадрат коэффициента подобия, т. е. 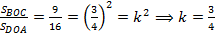 . Тогда отношение всех элементов этих треугольников равно
. Тогда отношение всех элементов этих треугольников равно 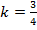 . А именно,
. А именно, 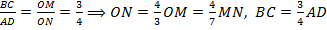 .
.
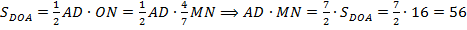 .
.
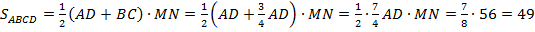 .
.
Ответ: 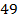 .
.
8. (182) В трапеции  основание
основание  вдвое больше основания
вдвое больше основания  и вдвое больше боковой стороны
и вдвое больше боковой стороны 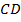 . Угол
. Угол  равен
равен 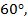 сторона
сторона 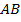 равна
равна 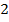 . Найдите площадь трапеции.
. Найдите площадь трапеции.
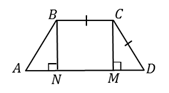 Решение.
Решение.
Так как 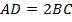 и
и 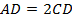 , то
, то 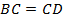 .
.
Проведём высоты 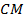 и
и 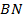 к основанию
к основанию  . Тогда
. Тогда 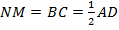 .
.
В 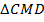
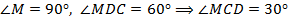 (по сумме углов треугольника). Значит, по свойству угла, равного
(по сумме углов треугольника). Значит, по свойству угла, равного 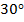 в прямоугольном треугольнике,
в прямоугольном треугольнике, 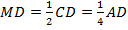 .
.
Тогда, 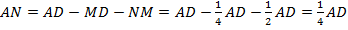 , т. е.
, т. е. 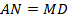 .
.
Рассмотрим 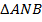 и
и  .
.
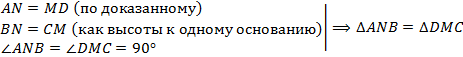 по I признаку равенства треугольников. Значит,
по I признаку равенства треугольников. Значит, 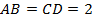 . Тогда
. Тогда 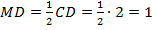 .
.
По определению косинуса острого угла в прямоугольном треугольнике 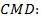
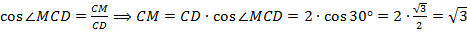 .
.
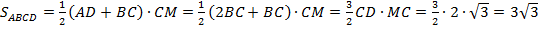 .
.
Ответ: 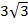 .
.
9. 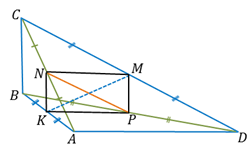 (311711) В выпуклом четырёхугольнике
(311711) В выпуклом четырёхугольнике  длина отрезка, соединяющего середины сторон
длина отрезка, соединяющего середины сторон 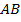 и
и 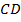 , равна одному метру. Прямые
, равна одному метру. Прямые  и
и  перпендикулярны. Найдите длину отрезка, соединяющего середины диагоналей
перпендикулярны. Найдите длину отрезка, соединяющего середины диагоналей 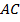 и
и 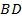 .
.
Решение.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|