
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
I способ. 1 страница
I способ.
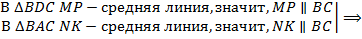
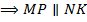 .
.
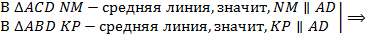
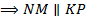 .
.
Значит, четырёхугольник KNMP является параллелограммом.
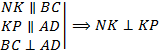 . Так как в параллелограмме KNMP один угол прямой, то этот параллелограмм является прямоугольником (противоположные углы равны и сумма односторонних равна 180°). Поскольку диагонали прямоугольника равны, то
. Так как в параллелограмме KNMP один угол прямой, то этот параллелограмм является прямоугольником (противоположные углы равны и сумма односторонних равна 180°). Поскольку диагонали прямоугольника равны, то 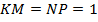 м
м
II способ.
Воспользуемся методом координат. Так как  , то
, то  лежит на оси ординат
лежит на оси ординат
( 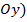 , а
, а  – на оси абсцисс
– на оси абсцисс 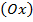 . Тогда вершины четырёхугольника
. Тогда вершины четырёхугольника  имеют координаты:
имеют координаты: 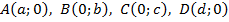 . По формулам координат середины отрезка найдём координаты точек
. По формулам координат середины отрезка найдём координаты точек 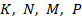 .
.
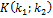
| 
| 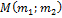
| 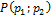
|
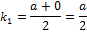
| 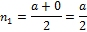
| 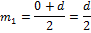
| 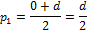
|
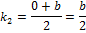
| 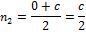
| 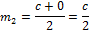
| 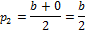
|
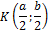
| 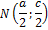
| 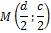
| 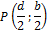
|
Теперь, по формуле расстояния между точками, найдём длины отрезков 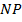 и
и 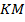 .
.
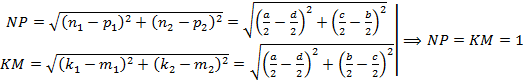 .
.
Обратим внимание, что 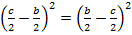 .
.
Ответ: 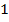 м.
м.
10.  (340409) В выпуклом четырёхугольнике
(340409) В выпуклом четырёхугольнике 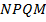 диагональ
диагональ 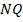 является биссектрисой угла
является биссектрисой угла 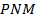 и пересекается с диагональю
и пересекается с диагональю 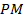 в точке
в точке 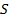 . Найдите
. Найдите 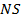 , если известно, что около четырёхугольника
, если известно, что около четырёхугольника 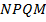 можно описать окружность,
можно описать окружность, 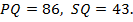
Решение.
Диагональ 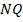 является биссектрисой
является биссектрисой 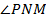 , значит,
, значит, 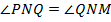 . Так как четырёхугольник вписан в окружность, то его стороны являются хордами этой окружности, а его углы – вписанными углами окружности. По свойству вписанных углов: «Вписанные углы, опирающиеся на одну и ту же хорду, и расположенные по одну сторону от этой хорды, равны», определяем, что
. Так как четырёхугольник вписан в окружность, то его стороны являются хордами этой окружности, а его углы – вписанными углами окружности. По свойству вписанных углов: «Вписанные углы, опирающиеся на одну и ту же хорду, и расположенные по одну сторону от этой хорды, равны», определяем, что  (они опираются на хорду
(они опираются на хорду 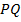 ), а
), а 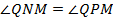 (они опираются на хорду
(они опираются на хорду 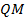 ). Но т. к.
). Но т. к. 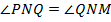 , то
, то 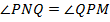 . Рассмотрим
. Рассмотрим 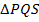 и
и 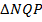 .
.
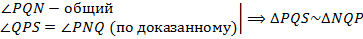 по I признаку подобия треугольников. Значит, соответственные стороны этих треугольников пропорциональны, т. е.
по I признаку подобия треугольников. Значит, соответственные стороны этих треугольников пропорциональны, т. е.
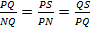 . Рассмотрим первое и третье отношение в этой пропорции.
. Рассмотрим первое и третье отношение в этой пропорции.
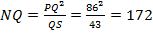 . Тогда,
. Тогда, 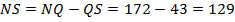 .
.
Ответ: 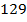 .
.
11.  (311717) Каждое основание
(311717) Каждое основание  и
и  трапеции
трапеции  продолжено в обе стороны. Биссектрисы внешних углов
продолжено в обе стороны. Биссектрисы внешних углов  и
и  в этой трапеции пересекаются в точке
в этой трапеции пересекаются в точке 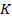 , биссектрисы внешних углов
, биссектрисы внешних углов 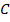 и
и 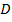 пересекаются в точке
пересекаются в точке 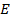 . Найдите периметр трапеции
. Найдите периметр трапеции  , если длина отрезка
, если длина отрезка 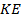 равна 28.
равна 28.
Решение.
I способ. Разберём рисунок. 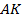 – биссектриса угла
– биссектриса угла 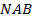 ,
, 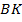 – биссектриса угла
– биссектриса угла 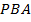 ,
, 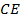 – биссектриса угла
– биссектриса угла 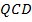 и
и 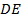 – биссектриса угла
– биссектриса угла 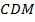 . Значит,
. Значит, 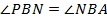 , но
, но 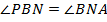 как накрест лежащие при параллельных прямых
как накрест лежащие при параллельных прямых  и
и  . Следовательно,
. Следовательно, 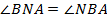 , и треугольник
, и треугольник 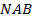 – равнобедренный, т. е.
– равнобедренный, т. е. 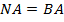 . Кроме того, в этом равнобедренном треугольнике биссектриса
. Кроме того, в этом равнобедренном треугольнике биссектриса 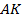 является и медианой, и высотой. Значит,
является и медианой, и высотой. Значит, 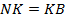 .
.
Аналогично, 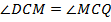 , но
, но 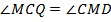 как накрест лежащие при параллельных прямых
как накрест лежащие при параллельных прямых  и
и  . Следовательно,
. Следовательно, 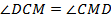 , и треугольник
, и треугольник 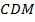 – равнобедренный, т. е.
– равнобедренный, т. е. 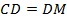 . Кроме того, в этом равнобедренном треугольнике биссектриса
. Кроме того, в этом равнобедренном треугольнике биссектриса 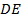 является и медианой, и высотой. Значит,
является и медианой, и высотой. Значит, 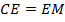 .
.
Так как точки 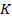 и
и 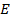 являются серединами сторон
являются серединами сторон 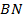 и
и 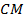 соответственно, то
соответственно, то 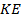 – средняя линия трапеции
– средняя линия трапеции  , поэтому,
, поэтому, 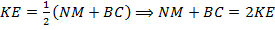 .
.
Теперь составим формулу для нахождения периметра трапеции  .
.
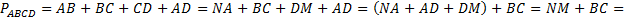
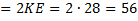 .
.
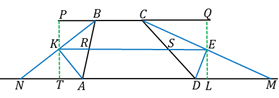
II способ. 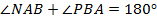 по свойству внутренних односторонних углов при параллельных прямых
по свойству внутренних односторонних углов при параллельных прямых  и
и  . Т. к.
. Т. к. 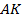 – биссектриса
– биссектриса 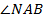 , то
, то  ;
; 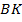 – биссектриса
– биссектриса 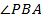 , значит,
, значит, 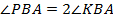 . Тогда,
. Тогда,
 . По сумме углов треугольника,
. По сумме углов треугольника,
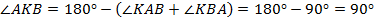 , т. е.
, т. е. 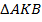 – прямоугольный.
– прямоугольный.
Аналогично, 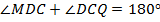 по свойству внутренних односторонних углов при параллельных прямых
по свойству внутренних односторонних углов при параллельных прямых  и
и  . Т. к.
. Т. к. 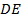 – биссектриса
– биссектриса 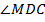 , то
, то 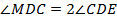 ;
; 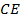 – биссектриса
– биссектриса 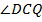 , значит,
, значит, 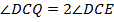 . Тогда,
. Тогда,
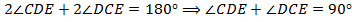 . По сумме углов треугольника,
. По сумме углов треугольника,
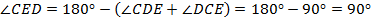 , т. е.
, т. е. 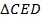 – прямоугольный.
– прямоугольный.
Так как точки  и
и 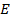 являются точками пересечения биссектрис внешних углов трапеции, то точка
являются точками пересечения биссектрис внешних углов трапеции, то точка 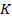 равноудалена от сторон
равноудалена от сторон 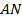 и
и 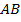 угла
угла 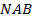 , а точка
, а точка 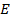 равноудалена от сторон
равноудалена от сторон 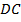 и
и 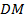 угла
угла 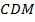 . Т. е., точки
. Т. е., точки 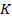 и
и 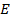 равноудалены от прямых
равноудалены от прямых  и
и 
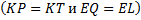 . Это означает, что
. Это означает, что 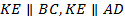 . Теперь воспользуемся теоремой Фалеса: «Две пары параллельных прямых, отсекающие на одной секущей равные отрезки, отсекают на любой другой секущей также равные отрезки». Значит,
. Теперь воспользуемся теоремой Фалеса: «Две пары параллельных прямых, отсекающие на одной секущей равные отрезки, отсекают на любой другой секущей также равные отрезки». Значит, 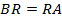 и
и 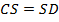 . Поэтому
. Поэтому 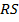 – средняя линия трапеции
– средняя линия трапеции  , и
, и 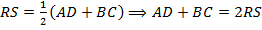 .
.
В 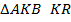 – медиана, опущенная из прямого угла, значит,
– медиана, опущенная из прямого угла, значит, 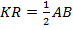 (в прямоугольном треугольнике центр окружности, описанной около треугольника, лежит на середине гипотенузы, поэтому
(в прямоугольном треугольнике центр окружности, описанной около треугольника, лежит на середине гипотенузы, поэтому 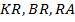 являются радиусами этой окружности). Следовательно,
являются радиусами этой окружности). Следовательно, 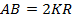 . Также, в
. Также, в 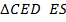 – медиана, опущенная из прямого угла, значит,
– медиана, опущенная из прямого угла, значит, 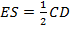 , значит,
, значит, 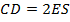 .
.
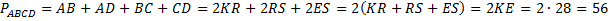 .
.
Ответ: 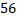 .
.
12.  (311712) Найдите площадь выпуклого четырёхугольника с диагоналями
(311712) Найдите площадь выпуклого четырёхугольника с диагоналями 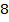 и
и 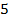 , если отрезки, соединяющие середины его противоположных сторон, равны.
, если отрезки, соединяющие середины его противоположных сторон, равны.
Решение.
Точки 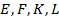 – середины сторон
– середины сторон 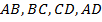 соответственно. Значит,
соответственно. Значит, 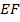 – средняя линия
– средняя линия 
 – средняя линия
– средняя линия 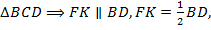
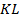 – средняя линия
– средняя линия 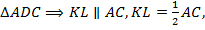
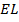 – средняя линия
– средняя линия 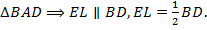
Тогда 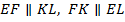 и четырёхугольник
и четырёхугольник 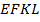 является параллелограммом. По условию известно, что его диагонали
является параллелограммом. По условию известно, что его диагонали 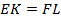 . Равенство диагоналей в параллелограмме является признаком прямоугольника. Значит,
. Равенство диагоналей в параллелограмме является признаком прямоугольника. Значит, 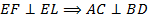 (т. к.
(т. к. 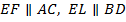 ). Находим площадь исходного четырёхугольника.
). Находим площадь исходного четырёхугольника.
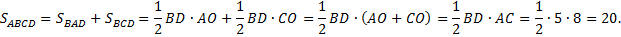
Ответ: 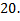
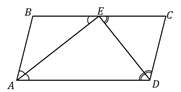
13. (339611, 339403) Биссектрисы углов 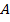 и
и  параллелограмма
параллелограмма  пересекаются в точке, лежащей на стороне
пересекаются в точке, лежащей на стороне  . Найдите
. Найдите  , если
, если  .
.
 Решение.
Решение.
 – биссектриса
– биссектриса 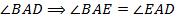 .
.
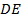 – биссектриса
– биссектриса 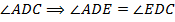 .
.
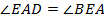 по свойству внутренних накрест лежащих при параллельных прямых
по свойству внутренних накрест лежащих при параллельных прямых  и
и  .
.
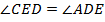 по свойству внутренних накрест лежащих при параллельных прямых
по свойству внутренних накрест лежащих при параллельных прямых  и
и  .
.
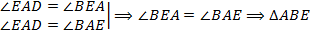 – равнобедренный, и
– равнобедренный, и 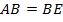 .
.
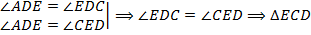 – равнобедренный, и
– равнобедренный, и 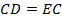 .
.
По свойству сторон параллелограмма (противоположные стороны параллелограмма равны), 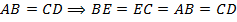 . Значит,
. Значит, 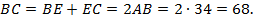
Ответ: 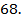
14. 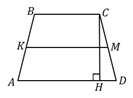 (128, 315116) В трапеции
(128, 315116) В трапеции  боковые стороны
боковые стороны 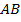 и
и 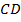 равны,
равны,  – высота, проведённая к большему основанию
– высота, проведённая к большему основанию  . Найдите длину отрезка
. Найдите длину отрезка 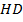 , если средняя линия
, если средняя линия 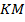 трапеции равна
трапеции равна 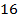 , а меньшее основание
, а меньшее основание  равно
равно 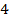 .
.
Решение.
Так как 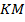 – средняя линия трапеции, то
– средняя линия трапеции, то 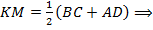
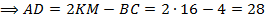 .
.
По условию, трапеция равнобедренная ( 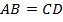 ), значит, отрезки, отсекаемые высотами, опущенными к большему основанию, равны. Тогда
), значит, отрезки, отсекаемые высотами, опущенными к большему основанию, равны. Тогда 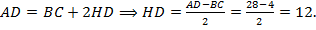
Ответ: 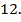
15. 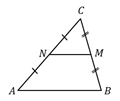 (339511) В треугольнике
(339511) В треугольнике  отмечены середины
отмечены середины  и
и  сторон
сторон  и
и 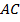 соответственно. Площадь треугольника
соответственно. Площадь треугольника 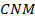 равна
равна 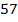 . Найдите площадь четырёхугольника
. Найдите площадь четырёхугольника 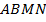 .
.
Решение.
Так как точки 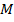 и
и 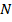 - середины сторон
- середины сторон  и
и 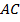 соответственно, то
соответственно, то 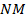 – средняя линия треугольника
– средняя линия треугольника 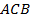 . Значит,
. Значит, 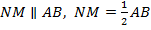 .
.
Рассмотрим 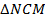 и
и 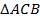
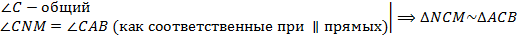 по I признаку подобия треугольников. Значит, стороны этих треугольников пропорциональны, т. е.
по I признаку подобия треугольников. Значит, стороны этих треугольников пропорциональны, т. е. 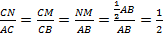 . Другими словами, коэффициент подобия этих треугольников равен
. Другими словами, коэффициент подобия этих треугольников равен 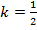 . Подобные треугольники обладают ещё тем свойством, что их площади относятся, как квадрат коэффициента подобия, т. е.
. Подобные треугольники обладают ещё тем свойством, что их площади относятся, как квадрат коэффициента подобия, т. е. 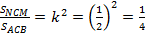 . Отсюда:
. Отсюда: 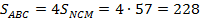 . Теперь можно найти площадь четырёхугольника
. Теперь можно найти площадь четырёхугольника 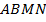 :
: 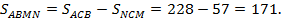
Ответ: 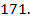
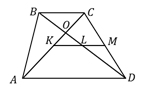
16. (311860, 316270) Основания трапеции 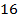 и
и 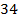 . Найдите отрезок, соединяющий середины диагоналей трапеции.
. Найдите отрезок, соединяющий середины диагоналей трапеции.
 Решение.
Решение.
I способ. Пусть  и
и 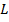 – середины диагоналей
– середины диагоналей 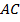 и
и 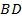 трапеции
трапеции  соответственно. Отметим точку
соответственно. Отметим точку 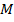 – середину стороны
– середину стороны 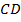 трапеции, и соединим её с точкой
трапеции, и соединим её с точкой 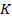 . Тогда в
. Тогда в 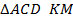 – средняя линия. По свойству средней линии треугольника: «Средняя линия треугольника, соединяющая две стороны, параллельна третьей стороне и равна её половине»
– средняя линия. По свойству средней линии треугольника: «Средняя линия треугольника, соединяющая две стороны, параллельна третьей стороне и равна её половине» 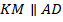 . Так как в трапеции основания параллельны, то
. Так как в трапеции основания параллельны, то 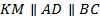 и
и 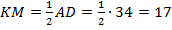 . Аналогично,
. Аналогично, 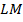 – средняя линия
– средняя линия 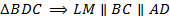 и
и 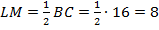 .
.
По аксиоме планиметрии: «Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной», прямые 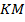 и
и 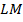 совпадают, т. е. точки
совпадают, т. е. точки 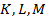 лежат на одной прямой, параллельной основаниям трапеции. Тогда,
лежат на одной прямой, параллельной основаниям трапеции. Тогда,
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|