ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ. 1.Производная суммы равна сумме производных. 2.Постоянный множитель можно выносить за знак производной. 3.Производная произведения. 4.Производная частного. 5.Производная сложной функции. 6.Производная корня. Домашнее задание.

ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ

1. Производная суммы равна сумме производных

2. Постоянный множитель можно выносить за знак производной

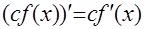3. Производная произведения

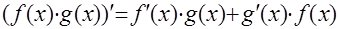4. Производная частного

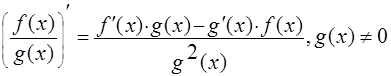5. Производная сложной функции

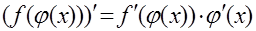6. Производная корня

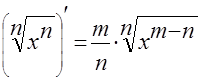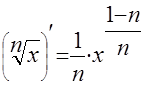Пример

Найти производную функции y=3x⁴

Решение

Представленная функция является степенной. «3» - постоянный множитель, который можно будет вынести за знак производной.

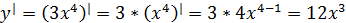
Пример 4.

Найти производную функции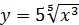

Решение

Вначале радикал преобразуем в степень

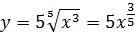
Затем находим производную от степенной функции

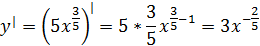
Пример 5.

Для функции 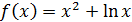, вычислите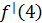

Решение

Здесь требуется вычислить значение производной в точке x=4.

1) используя правила и формулы дифференцирования, находим производную

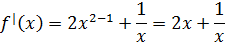
2) подставляем в найденную производную «4»

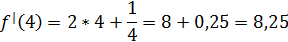
Домашнее задание.

1. Прочитать учебник п. 44, 45, опорный конспект в тетрадь.

2. посмотреть видеоурок https: //www. youtube. com/watch? v=dWvK76xZVT4

3. решить упр. № 787-790, 703(