
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Производная - предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю.
Производная - предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю.
На обычном языке:
Производная – скорость изменения функции в точке x0.
Рассмотрим на графики трех функций:
Какая из кривых растет быстрее?
Ответ, кажется, очевиден 1 кривая растет быстрее остальных. Мы смотрим, насколько круто идет вверх график функции. Другими словами — насколько быстро меняется ордината при изменении аргумента х. Одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.
Дифференцирование функции
Если функции y=f(x) имеет производную в точке x, то ее называют дифференцируемой в точке x.
Процесс нахождения производной называют дифференцированием функции y=f(x).
Если функция дифференцируема в некоторой точке, тогда к графику функции в этой точке можно провести касательную. Функция не может иметь разрыв в этой точки, тогда просто напросто нельзя провести касательную.
Если функция дифференцируема в точке x, то она непрерывна в этой точке.
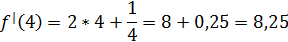
Опорный конспект. Производная функции.
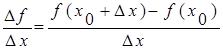 Определение: Производной функции f в точке x0 называетсячисло, к которому
Определение: Производной функции f в точке x0 называетсячисло, к которому
стремится разностное отношение
при х стремящемся к нулю.
ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
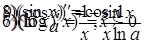
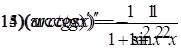
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|