Точки максимума и минимума – точки экстремума.

⇐ ПредыдущаяСтр 3 из 3

Функция может иметь неограниченное количество экстремумов.

Критическая точка – это точка, производная в которой равна 0 или не существует.

Важно помнить, что любая точка экстремума является критической точкой, но не всякая критическая является экстремальной.

Алгоритм исследования функции на монотонность и экстремумы:

1) Найти область определения функции D(f)

2) Найти производную f' (x).

3) Найти стационарные (f'(x) = 0) и критические (f'(x) не существует) точки функции y = f(x).

4) Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.

5) Сделать выводы о монотонности функции и точках ее экстремума.

Пример 1. Определите промежуток монотонности функции у=х²-8х +5

Решение: Найдем производную заданной функции: у’=2x-8

2x-8=0

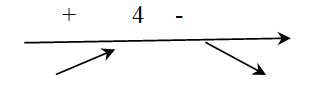
х=4

Определяем знак производной функции и изобразим на рисунке, следовательно, функция возрастает при хϵ (4; +∞ ); убывает при хϵ (-∞; 4)

Ответ: возрастает при хϵ (4; +∞ ); убывает при хϵ (-∞; 4)

Пример 2. Найдите точку минимума функции у= 2х-ln(х+3)+9

Решение: Найдем производную заданной функции: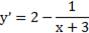

Найдем нули производной: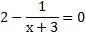

х=-2, 5

Определим знаки производной функции и изобразим на рисунке поведение функции:

Ответ: -2, 5 точка min

Пример 3. На рисунке изображен график функции. На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7. Определите количество целых точек, в которых производная функции отрицательна.

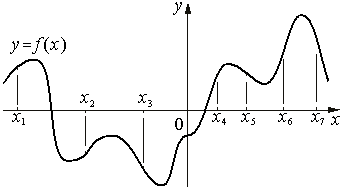
Решение: Производная функции отрицательна на тех интервалах, на которых функция убывает. В данном случае это точки х3, х5, х7. Следовательно, таких точек 3

Ответ: 3

⇐ Предыдущая 1 23