2. Экстремумы функции.. Возрастание функции.

2. Экстремумы функции.

Возрастание функции.

Функция y=f(x) возрастает на интервале X, если для любых х₁ и х₂, 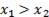из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Максимум функции. Значение функции в точке максимума называют максимумом функции

Минимум функции. Значение функции в точке минимума называют минимумом функции

Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).

Точка максимума функции. Точку х₀ называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .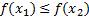

Точка минимума функции. Точку х₀ называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .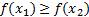

Точки экстремума функции. Точки минимума и максимума называют точками экстремума.

Убывание функции. Функция y = f(x) убывает на интервале X, если для любых х₁ и х₂, 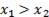из этого промежутка выполняется неравенство 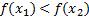. Другими словами – большему значению аргумента соответствует большее значение функции.

Точки, в которых происходит изменение характера монотонности функции – это ТОЧКИ ЭКСТРЕМУМА.

Точку х = х₀ называют точкой минимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≥ f(x₀).

Точку х = х₀ называют точкой максимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≤ f(x₀).

⇐ Предыдущая 123 Следующая ⇒