
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
1. Возрастание и убывание функции.
Лекция 22. «Возрастание и убывание функции на интервале. Критические точки. Экстремумы функции»
1. Возрастание и убывание функции.
Алгоритм нахождения промежутков возрастания и убывания функции y = f(x)
1. Найти D(f) – область определения.
2. Найти f‘(x) – производную.
3. Определить, при каких значениях х производная f‘(x) ≥ 0 (на этих промежутках функция возрастает); при каких значениях х производная f‘(x) ≤ 0 (на этих промежутках функция убывает))
Функция y = f(x), определенная на промежутке Х, называется возрастающей на этом промежутке, если для любой пары чисел х1 и х2 из этого промежутка из неравенства х1< х2 следует неравенство f(x1) < f(x2)
Функция y = f(x), определенная на промежутке Х, называется убывающей на этом промежутке, если для любой пары чисел х1 и х2 из этого промежутка из неравенства х1< х2 следует неравенство f(x1) > f(x2)
Теоремы
1. Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≥ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек), то функция y = f(x) возрастает на промежутке Х.
2. Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≤ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек), то функция y = f(x) убывает на промежутке Х.
Пример 1. Определите промежутки монотонности функции
у = -3х3 + 4х2 + х – 10.
Решение
1. Найдем область определения функции.
D(y) = 
2. Найдем производную функции.
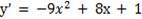
y’ = (x – 1)(-9x – 1)
3. Определим, на каких промежутках производная положительна (на этих промежутках функция возрастает), на каких – отрицательна (на этих промежутках функция убывает).
Применим для этого метод интервалов. Для определения знака на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
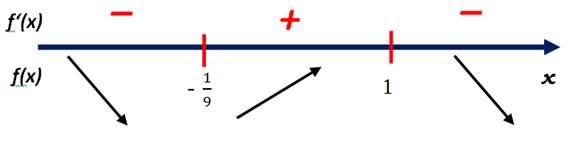
Так как на интервале 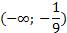 производная функции отрицательна, то на этом интервале функция убывает.
производная функции отрицательна, то на этом интервале функция убывает.
Так как на интервале 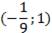 производная функции положительна, то на этом интервале функция возрастает.
производная функции положительна, то на этом интервале функция возрастает.
Так как на интервале 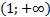 производная функции отрицательна, то на этом интервале функция убывает.
производная функции отрицательна, то на этом интервале функция убывает.
Так как в точках 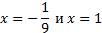 функция непрерывна, то эти точки входят в промежутки возрастания и убывания данной функции.
функция непрерывна, то эти точки входят в промежутки возрастания и убывания данной функции.
Следовательно, функция возрастает на 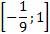 ; функция убывает на
; функция убывает на  и на
и на 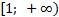 .
.
Ответ: Функция возрастает на 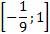
Функция убывает на  и на
и на 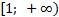 .
.
Пример 2. Определите промежутки монотонности функции
у = х5–5х4 +5х3 – 4.
Решение:
1. 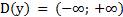
2. 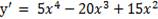
y ' = 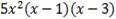
1. Функция возрастает на 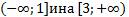 ; функция убывает на
; функция убывает на 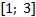 .
.
Ответ: Функция возрастает на 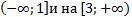 ;
;
функция убывает на 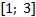 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|