Контакты

Случайная статья

3. Матричный способ. Рассмотрим систему вида

⇐ ПредыдущаяСтр 3 из 3

3. Матричный способ

Систему можно решить и матричным способом.

Рассмотрим систему вида

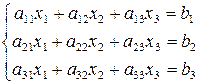
(4)

Составим матрицу системы из коэффициентов при неизвестных:

.

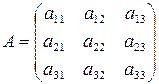Из неизвестных 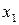, , 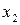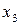и свободных членов составим матрицы – столбцы

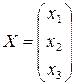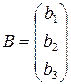; (5)

Тогда система (4) в матричной форме примет вид

.

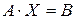Чтобы найти матрицу 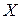, умножим (5) на 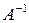слева.

A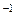

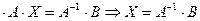
Пример 4.

.

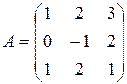Найти обратную матрицу .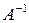

РЕШЕНИЕ.

1) Составляем и вычисляем определитель

.

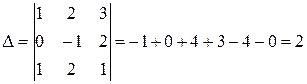2) Транспонируем матрицу. Получаем

.

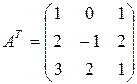3) Вычисляем алгебраические дополнения

; ; ; ; ; ; ; ; .

;

. . ;

; ; ; ; ; .

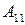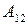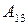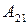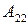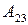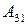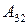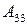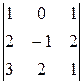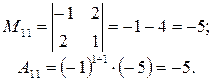
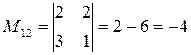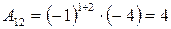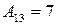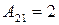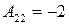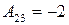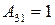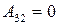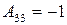Составим обратную матрицу

A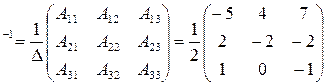

A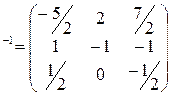

Пример 5.

Решить систему матричным способом

.

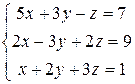Из коэффициентов при неизвестных составим матрицу :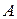

.

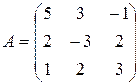Из неизвестных составим матрицу – столбец:

.

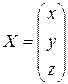Из свободных членов составим матрицу – столбец:

.

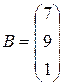Тогда система запишется в виде

.

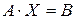Получили матричное уравнение. Умножаем обе части этого уравнения на 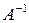слева. Получаем:

.

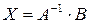Находим обратную матрицу:

; ;

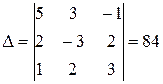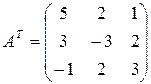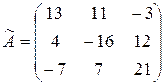(матрица, составленная из алгебраических дополнений элементов; 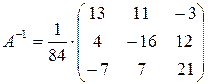(обратная матрица).

Умножая обратную матрицу на 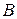, получаем матрицу .

.

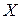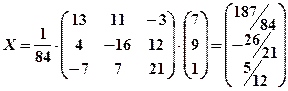Отсюда получаем ответ:

; ; .

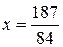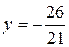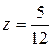Сравните решение этой системы с решением метода Гаусса.

⇐ Предыдущая 1 23

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.