
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
3. Метод Гаусса
Эффективным методом решения и исследования систем линейных уравнений является метод последовательного исключения неизвестных, или метод Гаусса.
Идея метода Гаусса состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему специального вида, которая легко исследуется и решается.
Пример 3.
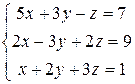 .
.
В результате элементарных преобразований добиваются того, чтобы в последнем уравнении системы осталось одно неизвестное ( 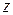 ), во втором – 2 неизвестных (
), во втором – 2 неизвестных ( 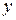 и
и 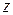 ) а в первом – 3 неизвестных (
) а в первом – 3 неизвестных ( 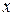 ,
, 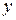 ,
, 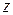 ). За ведущее уравнение берется то, в котором коэффициент при
). За ведущее уравнение берется то, в котором коэффициент при 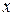 равен 1. Если такого уравнения нет, то его легко получить, разделив любое из уравнений системы на коэффициент при
равен 1. Если такого уравнения нет, то его легко получить, разделив любое из уравнений системы на коэффициент при 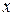 .
.
Ведущим уравнением данной системы будет последнее. Перепишем систему так:
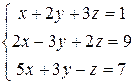 (2)
(2)
Умножаем первое уравнение на (-2) и складываем со вторым, чтобы избавиться от 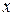 во втором уравнении. Результат сложения записываем на месте второго уравнения. Далее первое уравнение умножаем на (-5) и складываем с третьим, чтобы избавиться от
во втором уравнении. Результат сложения записываем на месте второго уравнения. Далее первое уравнение умножаем на (-5) и складываем с третьим, чтобы избавиться от 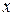 в третьем уравнении. Результат записываем на месте третьего уравнения. Первое уравнение при этом переписываем без изменений. Получим:
в третьем уравнении. Результат записываем на месте третьего уравнения. Первое уравнение при этом переписываем без изменений. Получим:
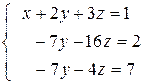 (3)
(3)
Умножаем второе уравнение системы (5) на (-1) и складываем с третьим, чтобы избавиться от 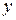 в третьем уравнении.
в третьем уравнении.
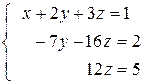 .
.
Из последнего уравнения 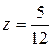 . Подставляем это значение
. Подставляем это значение 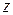 во втрое уравнение системы и находим
во втрое уравнение системы и находим 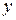 :
:
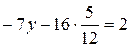
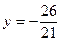 .
.
В первое уравнение подставляем значения 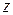 и
и 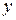 , получаем
, получаем
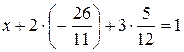
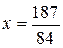 .
.
Ответ: 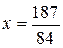 ;
; 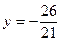 ;
; 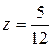 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|