Урок - лекция. 1. Орг. момент. 2. Изучение нового материала (лекция с элементами беседы). 1. Системы линейных уравнений. (общие сведения). 2. Метод Крамера

Урок - лекция

Тема: Метод Гаусса для решения системы линейных уравнений (последовательного исключения неизвестных). Правило Крамера для решения квадратной системы линейных уравнений. Существование и единственность решения системы. Метод Крамера в матричной форме.

Цель: познакомить студентов с различными методами для решения систем линейных алгебраических уравнений

План

1. Орг. момент

2. Изучение нового материала (лекция с элементами беседы)

1. Системы линейных уравнений

(общие сведения)

Пусть задана система 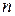линейных уравнений с 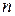неизвестными

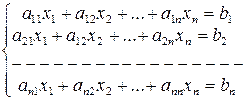(1)

Решением системы (1) называется совокупность чисел ( 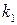, , 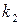…, 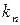), которая при подстановке в систему (1) вместо неизвестных обращает каждое уравнение системы в тождество. Система может иметь решение, тогда она называется совместной, причем, если решение единственное, система определенная, если решений множество – система неопределенная. Если система не имеет решений, она называется несовместной. Рассмотрим два способа решения системы: метод Крамера и метод Гаусса.

2. Метод Крамера

При решении методом Крамера используем определители 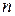-го порядка. Пусть задана система (1). Составим главный определитель системы из коэффициентов при неизвестных:

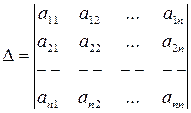ТЕОРЕМА. Если определитель системы 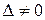, то систему (3) можно решить по формуле Крамера, причем это решение единственное:

; ; …; ,

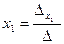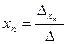где определитель 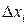может быть получен из главного определителя путем замены 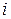-го столбца на столбец из свободных членов.

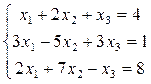Пример 1.

Составляем главный определитель, элементами которого являются коэффициенты при неизвестных. Вычислим все четыре определителя.

;

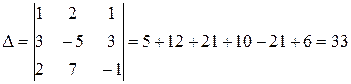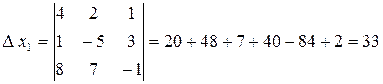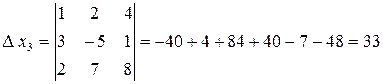Неизвестные 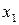, , 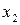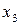находим по формулам

; ; ;

; ; .

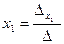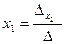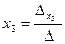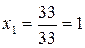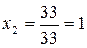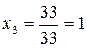Ответ: ; ; .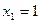

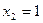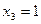Пример2. Решить систему 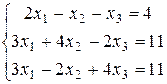методом Крамера.

Решение. Выписываем A - матрицу системы и B - столбец свободных членов: 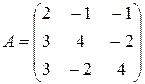, . Далее вычисляем определители:

;

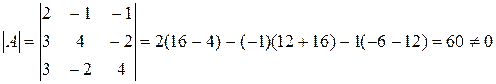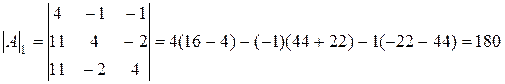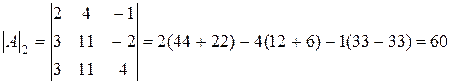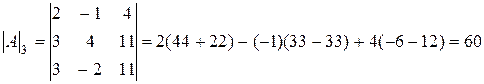По теореме Крамера 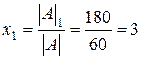; ; 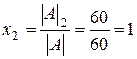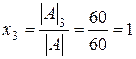. Ответ: ; ; .

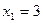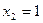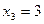Для проверки результата подставим полученные значения неизвестных в каждое уравнение системы: 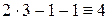, , 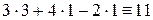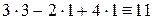. Все уравнения обратились в тождества, значит, решение найдено верно.

Условия неопределенности и несовместности системы двух линейных уравнений с двумя переменными.

Если определитель системы 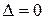, то система является либо несовместной (когда 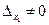и 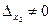), либо неопределенной (когда и 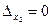). В последнем случае система сводится к одному уравнению, а другое является следствием этого уравнения.

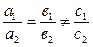Условия несовместности системы двух линейных уравнений с двумя переменными можно записать в виде:

Условия неопределенности системы двух линейных уравнений с двумя переменными можно записать в виде:

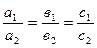Если один из вспомогательных определителей отличен от нуля, то система уравнений (1) не имеет решения (если ).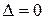

Если главный и все вспомогательные определители равны нулю, то система (1) имеет бесконечно много решений.

Если главный определитель отличен от нуля, то система уравнений (1) имеет единственное решение.

12 3 Следующая ⇒