Тема 14 задача 1

Тема 14 задача 1

Нахождение кратчайшего пути в графе.

Пусть дан граф, дугам которого приписаны веса. Задача о нахождении кратчайшего пути состоит в нахождении кратчайшего пути от заданной начальной вершины до заданной конечной вершины, при условии, что такой путь существует.

Можно дать много практических интерпретаций задачи о кратчайших путях. Например, вершины могут соответствовать городам и каждая дуга - некоторому пути, длина которого представлена весом дуги. Мы ищем кратчайшие пути между городами. Вес дуги может соответствовать стоимости (или времени) передачи информации между вершинами. В этом случае мы ищем самый дешевый (или самый скорый).

Данная задача может быть разбита на две:

1. Для начальной заданной вершины найти все кратчайшие пути от этой вершины к другим;

2. Найти кратчайшие пути между всеми парами вершин.

Рассмотрим алгоритм решения для задачи:

Необходимо найти путь от s - начальной вершины до t - конечной вершины. Каждой вершине присваиваем пометки I(Xi).

1. I(s) = 0, I(Xi) равно бесконечности для всех Хi не равных s и считать эти пометки временными. Положить р = s.

2. Для всех Хi, пренадлежащих Г(р) и пометки которых временны, изменить пометки по следующему правилу:

I(Xi) = min[I(Xi), I(p) + c(p, Xi)]

3. Среди всех вершин с временными пометками найти такую, для которой I(Xi*) = min[I(Xi)]

4. Считать пометку вешины Хi* постоянной и положить р = Хi*.

5. Если р = t, то I(р) является длинной кратчайшего пути, если нет, перейти к шагу 2.

Как только все пометки расставлены, кратчайшие пути получают, используя состношение I(Xi') + c(Xi',Xi) = I(Xi) (1).

Пример решения задачи.

Рассмотрим граф, изображенный на рисунке. Требуется найти все кратчайшие пути от вершины Х1 ко всем остальным вершинам. Матрица весов приведена ниже.

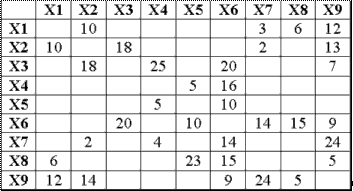
Решение:

I(X1)=0*, I(Xi)=∞, Xi≠X1, p=X1

1) Г{X1}=Г(X1)={X2,X7,X9}

I(X2)=min[∞, 0*+10]=10

I(X7)=min[∞, 0*+3]=3

I(X8)=min[∞, 0*+6]=6

I(X9)=min[∞, 0*+12]=12

min[I(X2), I(X3), I(X4), I(X5), I(X6), I(X7), I(X8), I(X9)]=3

X7:I(X7)=3*, p=3

2) Г{X7}=Г(X7)={X2,X4,X6,X9}

I(X2)=min[10, 3*+2]=5

I(X4)=min[∞, 3*+4]=7

I(X6)=min[∞, 3*+14]=17

I(X9)=min[12, 3*+24]=12

min[I(X2),I(X3),I(X4),I(X5),I(X6),I(X8),I(X9)]=5

X2:I(X2)=5*, p=5

3) Г{X2}=Г(X2)={X3,X9}

I(X3)=min[∞, 5*+18]=23

I(X9)=min[∞, 5*+13]=12

min[I(X3),I(X4),I(X5),I(X6),I(X8),I(X9)]=6

X8:I(X8)=6*, p=6

4) Г{X8}=Г(X8)=[X5,X6,X9]

I(X5)=min[∞, 6*+23]=29

I(X6)=min[17, 6*+15]=17

I(X9)=min[12,6*+5]=11

min[I(X3),I(X4),I(X5),I(X6),I(X9)]=7

X4:I(X4)=7*, p=7

5) Г{X4}=Г(X4)={X3,X5,X6}

I(X3)=min[23, 7*+25]=23

I(X5)=min[29, 7*+5]=12

I(X6)=min[17, 7*+16]=17

min[I(X3),I(X5),I(X6),I(X9)]=11

X9:I(X9)=11*, p=11

6) Г{X9}=Г(X9)={X6}

I(X6)=min[17, 11*+9]=17

min[I(X3),I(X5),I(X6)]=12

X5:I(X5)=12*, p=12

7) Г{X5}=Г(X5)={X6}

I(X6)=min[17, 12*10]=17

min[I(X3),I(X6)]=17

X6:I(X6)=17*, p=17

8) Г{X6}=Г(X6)={X3}

I(X3)=min[23, 17*+20]=23

X3:I(X3)=23*, p=23

Все вершины имеют пометки.

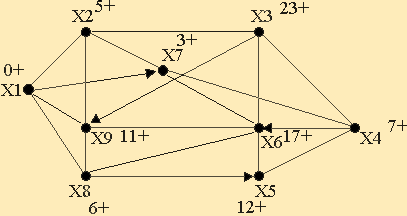
Найдём кратчайший путь, например, (Х1,Х2).

Вершина Х2 имеет пометку 5*. Полагая в соотношении (1) Хi = Х2, получаем I(X2')+с(Х2', Х2) = I(X2) = 5.

Единственной такой вершиной является Х7. Далее применяем ещё раз соотношение (1) и получаем путь (Х1,Х7,Х2) и т. д.

⇐ Предыдущая 123 Следующая ⇒