Тема 11 задача 1. Задача

Тема 11 задача 1

Нахождение минимального остова в графе.

Алгоритм решения

1. Упорядочить ребра графа по возрастанию весов;

2. Выбрать ребро с минимальным весом, не образующее цикл с ранее выбранными ребрами. Занести выбранное ребро в список ребер строящегося остова;

3. Проверить, все ли вершины графа вошли в построенный остов. Если нет, то выполнить пункт 2.

Задача

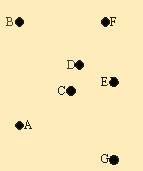Требуется спроектировать сеть, которая должна обслуживать семь населённых пунктов. Расстояния между пунктами приведены в таблице.

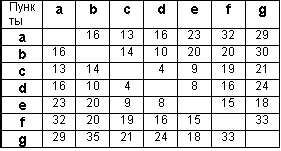
Решение

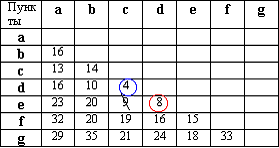
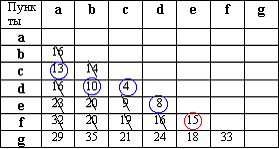
Для решения данной задачи достаточно рассмотреть или только левую или только правую часть от главной диагонали матрицы. Воспользуемся левой частью таблицы.

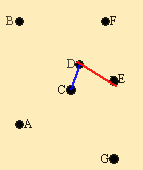
Из элементов матрицы выбираем минимальный - (D,С) = 4. Обводим выбранный элемент кружком.

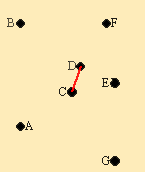
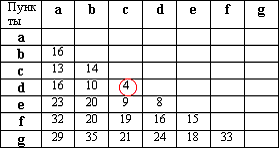
Из оставшихся элементов выбираем минимальный - (D,E) = 8. Элемент обводим кружком. Чтобы выполнялось условие 2 пункты С и D не должны соединяться, поэтому элемент (Е,С) зачёркивается.

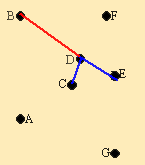
Из невыделенных и незачеркнутых элементов минимальным является (D,B). Этот элемент обводится кружком. Элементы (С,В) и (Е,В) зачёркиваются.

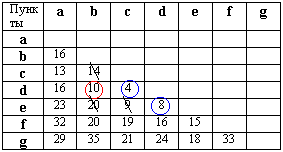
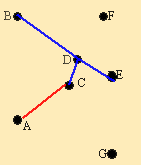Минимальным элементом является (С,А) = 13. Элементы (В,А), (D,А) и (Е,А) зачеркиваются.

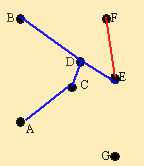
Из невыделенных и незачеркнутых элементов минимальным является (F,E) = 15. Элементы (F,A), (F,B), (F,C) и (F,D) зачёркиваются.

В последней строке минимальным элементом является (G,E) = 18. Обводим этот элемент, и получаем остов, связывающий все семь пунктов. Все остальные элементы вычеркиваются.

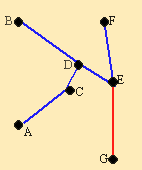
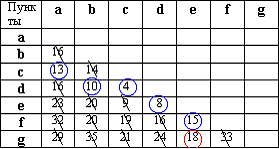
Длина минимального остова равна (С,А)+(D,B)+(D,С)+(Е,D)+(F,E)+(G,E) = 13+10+4+8+15+18 = 68.

12 3 Следующая ⇒