
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вычисление объема тела вращения с помощью определенного интеграла.
Вычисление объема тела вращения с помощью определенного интеграла.
Помимо нахождения площади плоской фигуры с помощью определенного интеграла важнейшим приложением темы является вычисление объема тела вращения. Для вычисления объема тела необходимо уметь решать неопределенные интегралы средней сложности и применять формулу Ньютона-Лейбница в определенном интеграле. Как и для задачи нахождения площади, нужны уверенные навыки построения чертежей – это чуть ли не самое важное.
Вообще в интегральном исчислении очень много интересных приложений, с помощью определенного интеграла можно вычислить площадь фигуры, объем тела вращения, длину дуги, площадь поверхности вращения и многое другое.
Представьте некоторую плоскую фигуру на координатной плоскости. Но, кроме того, данную фигуру можно ещё и вращать, причем вращать двумя способами:
– вокруг оси абсцисс ; – вокруг оси ординат .
Будут разобраны оба случая. Особенно интересен второй способ вращения, он вызывает наибольшие затруднения, но на самом деле решение практически такое же, как и в более распространенном вращении вокруг оси абсцисс.
Начнем с наиболее популярной разновидности вращения.
Вычисление объема тела, образованного вращением
плоской фигуры вокруг оси 
Пример 1
Вычислить объем тела, полученного вращением фигуры, ограниченной линиями 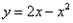 ,
, 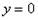 вокруг оси
вокруг оси 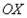 .
.
Решение: Как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. То есть, на плоскости 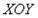 необходимо построить фигуру, ограниченную линиями
необходимо построить фигуру, ограниченную линиями 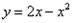 ,
, 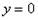 , при этом не забываем, что уравнение
, при этом не забываем, что уравнение 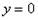 задаёт ось
задаёт ось 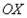 . .
. .
Чертёж здесь довольно прост:
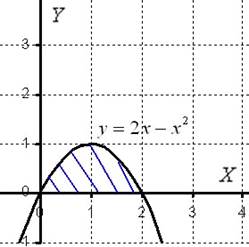
Искомая плоская фигура заштрихована синим цветом, именно она и вращается вокруг оси 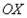 В результате вращения получается такая немного яйцевидная летающая тарелка, которая симметрична относительно оси
В результате вращения получается такая немного яйцевидная летающая тарелка, которая симметрична относительно оси 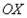 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|